Уравнение прямых на плоскости и их составление.

Всякую прямую на плоскости в прямоугольных координатах ХОУ можно описать линейным уравнением первого порядка относительно двух переменных: х и у.

О п р е д е л е н и е 1. Общим уравнением прямой на плоскости называется уравнение вида

Ax+By+C=0. (3.1)

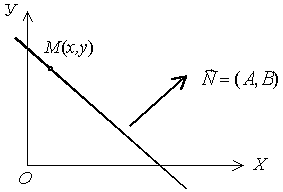Рис. 39

Здесь M (x,y) - координаты текущей точки прямой. Вектор 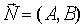перпендикулярен данной прямой (рис. 39).

О п р е д е л е н и е 2. Вектор 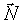, перпендикулярный прямой, называется нормальным вектором данной прямой. В качестве нормального вектора может быть взят любой вектор, перпендикулярный прямой.

Если на прямой задана фиксированная точка M (x₀,y₀) и нормальный вектор 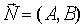, то уравнение прямой, проходящей через фиксированную точку M (x₀,y₀) перпендикулярно вектору 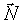имеет вид

A (x-x₀) + B ( y-y₀) = 0. (3.2)

Покажем, что уравнение (3.2) является общим уравнением прямой. Для этого раскроем скобки и запишем свободный член

A x + By + (-Ax₀ - By₀) = 0.

Обозначим C = -Ax₀ - By₀, получим уравнение (3.1)

Ax + By + C=0.

Задача 1. Составить уравнение прямой, проходящей через точку M₀ = (2, -3) перпендикулярно вектору .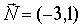

Решение. Будем использовать уравнение (3.2):

.

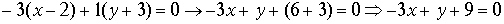Ответ: -3x + y + 9 = 0.

Задача 2. Составить уравнение прямой, проходящей через точку M₀ = (-1, 2) перпендикулярно оси ОХ.

Решение. Будем использовать уравнение (3.2). В качестве нормального вектора возьмем любой вектор, лежащий на оси ОХ, например, :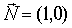

.

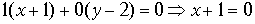Ответ: x + 1 = 0.

Прямая на плоскости может быть задана одним из уравнений:

1 ⁰. Общее уравнение прямой:

Ax + By + C = 0. (2.1)

Вектор n (А,В) ортогонален прямой, числа A и B одновременно не равны нулю.

2 ⁰. Уравнение прямой с угловым коэффициентом:

y - y _o = k (x - x _o ), (2.2)

где k - угловой коэффициент прямой, то есть k = tg a , где a - величина угла, образованного прямой с осью Оx, M (x _o, y _o ) - некоторая точка, принадлежащая прямой.

Уравнение (2.2) принимает вид y = kx + b, если M (0, b) есть точка пересечения прямой с осью Оy.

3 ⁰. Уравнение прямой в отрезках:

x/a + y/b = 1, (2.3)

где a и b - величины отрезков, отсекаемых прямой на осях координат.

4 ⁰. Уравнение прямой, проходящей через две данные точки - A(x ₁, y ₁ ) и B(x ₂, y ₂ ):

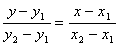. (2.4)

5 ⁰. Уравнение прямой, проходящей через данную точку A(x ₁, y ₁ ) параллельно данному вектору a (m, n):

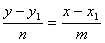. (2.5)

6 ⁰. Нормальное уравнение прямой:

rn^о - р = 0, (2.6)

где r - радиус-вектор произвольной точки M(x, y) этой прямой, n ^о - единичный вектор, ортогональный этой прямой и направленный от начала координат к прямой; р - расстояние от начала координат до прямой.

Окружность и эллипс.

Окружность. Окружностью называется геометрическое место точек, равноудаленных от одной и той же точки.

Уравнение окружности имеет вид

(x - a)² + (y - b)² = r²,

где a и b - координаты центра окружности, а r - радиус окружности. Если же центр окружности находится в начале координат, то ее уравнение имеет вид

x² + y² = r².

Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).

Простейшее уравнение эллипса

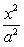
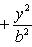
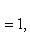
где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение

a² - b² = c².

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси

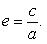
У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси.

Пример задач:Написать уравнение окружности с центром в точке C(2, -3) и радиусом, равным 6.

Показать, что x² + y² + 4x - 6y - 3 = 0 есть уравнение окружности. Найти ее центр и радиус.

Найти координаты центра и радиус окружности x² + y² - x + 2y - 1 = 0.

Дана окружность x² + y² = 4. Составить уравнение прямой l, параллельной оси абсцисс и пересекающей окружность в таких точках M и N, чтоMN = 1.

Найти длину хорды, образующейся при пересечении прямой x + y - 5 = 0 и окружности (x + 1)² + (y + 2)² = 40.

Найти точки пересечения окружности (x - 1)² + (y - 2)² = 4 и прямой y = 2x.

Написать уравнение окружности, проходящей через три точки: (0, 1); (2, 0); (3, -1).

Найти уравнение окружности, касающейся оси Ox в начале координат и пересекающей ось Oy в точке A(0, 10).

Составить простейшее уравнение эллипса, зная, что: а) его полуоси a = 6, b = 4; б) расстояние между фокусами 2c = 10, а большая полуось 2a = 16; в) большая полуось a = 12, а эксцентриситет e = 0,5; г) малая полуось b = 8, а эксцентриситет e = 0,6; д) сумма полуосей a + b = 12, а расстояние между фокусами 2c=6*2^1/2.

Найти длины осей, координаты фокусов и эксцентриситет эллипса 4x² + 9y² = 144.

Составить уравнение окружности, проходящей через точку A (2; 1) и касающейся осей координат.

Отрезок BC длины l движется своими концами по сторонам прямого угла BOC. Какую линию опишет на этом отрезке точка A, разделяющая его в отношении λ(BA/AC = λ)?

Составить уравнение окружности, вписанной в треугольник, стороны которого лежат на прямых x = 0, y = 0 и 3x + 4y - 12 = 0.

Составить уравнение окружности, описанной около треугольника, образованного прямой 3x - y + 6 = 0 и осями координат.

Гипербола.

Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемыхфокусами есть величина постоянная, меньшая расстояния между фокусами.

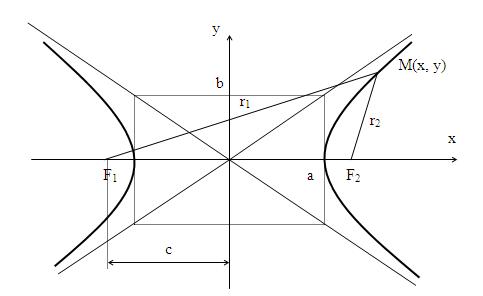
По определению | r ₁ – r ₂ | = 2 a . F ₁ , F ₂ – фокусы гиперболы. F ₁ F ₂ = 2 c .

Выберем на гиперболе произвольную точку М(х, у). Тогда :

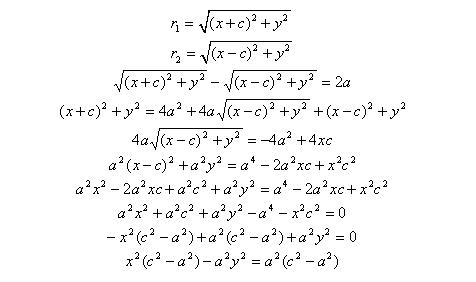
обозначим с² – а² = b² (геометрически эта величина – меньшая полуось)

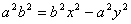
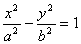
Получили каноническое уравнение гиперболы.Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью.

Ось 2 b называется мнимой осью.

Гипербола имеет две асимптоты, уравнения которых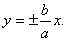

Определение. Отношение 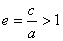называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с² – а ² = b²

:

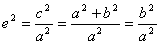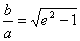
Если а = b , e = 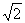, то гипербола называется равнобочной (равносторонней).

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: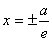

Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу.

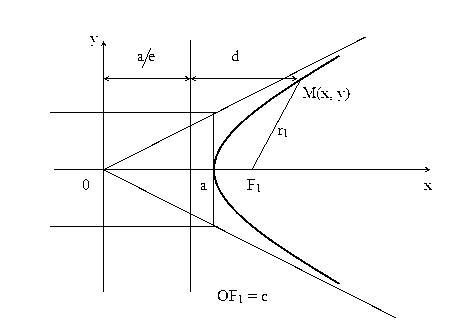
Из очевидных геометрических соотношений можно записать:

a / e + d = x , следовательно d = x – a / e .

( x – c ) ² + y² = r ²

Из канонического уравнения: 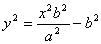, с учетом b² = c² – a²:

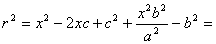
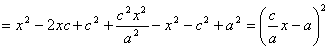
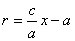
Тогда т.к. с/ a = e , то r = ex – a .

Итого: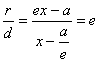

Для левой ветви доказательство аналогично. Теорема доказана

Пример 1 . Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса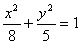

Для эллипса: c ² = a² – b² .
Для гиперболы: c² = a² + b² .

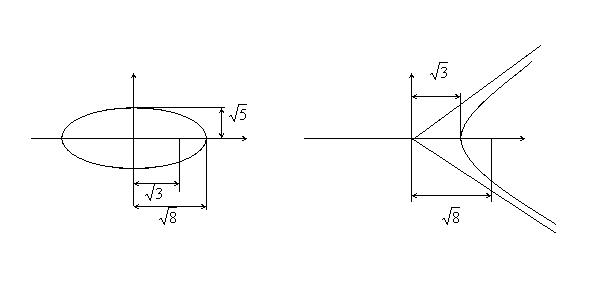
Уравнение гиперболы: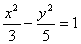

Пример 2 . Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением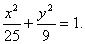

Находим фокусное расстояние c ² = 25 – 9 = 16.

Длягиперболы: c² = a² + b² = 16, e = c / a = 2; c = 2 a ; c ² = 4 a² ; a² = 4;

b² = 16 – 4 = 12.

Итого: 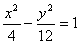- искомое уравнение.

Парабола.

Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса 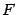опустим перпендикуляр 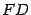на директрису 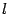. Начало координат 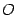расположим на середине отрезка 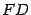, ось 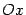направим вдоль отрезка 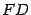так, чтобы ее направление совпадало с направлением вектора 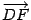. Ось 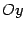проведем перпендикулярно оси 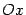(рис. 12.15).

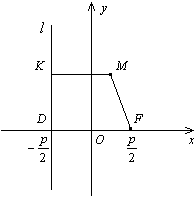
Рис.12.15.

Теорема 12.4 Пусть расстояние между фокусом 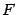и директрисой 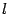параболы равно 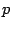. Тогда в выбранной системе координат парабола имеет уравнение

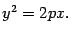(12.10)

Доказательство. В выбранной системе координат фокусом параболы служит точка 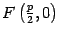, а директриса имеет уравнение 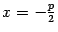(рис. 12.15).

Пусть 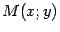-- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим

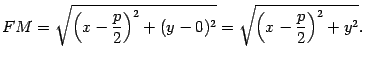
Расстоянием от точки 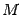до директрисы 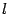служит длина перпендикуляра 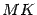, опущенного на директрису из точки 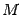. Из рисунка 12.15 очевидно, что 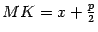. Тогда по определению параболы 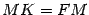, то есть

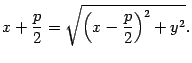
Возведем обе части последнего уравнения в квадрат:

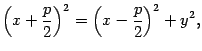
откуда

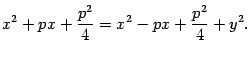
После приведения подобных членов получим уравнение (12.10).

Уравнение (12.10) называется каноническим уравнением параболы.

Предложение 12.4 Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью .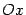

Доказательство. Проводится так же, как и доказательство (предложения 12.1).

Точка пересечения оси симметрии с параболой называется вершиной параболы.

Если переобозначить переменные 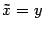, , 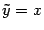то уравнение (12.10) можно записать в виде

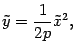
который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований (рис. 12.16).

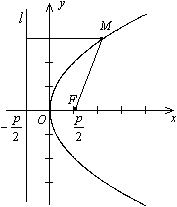
Рис.12.16.Парабола

Пример 12.6 Постройте параболу 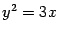. Найдите ее фокус и директрису.

Решение. Уравнение является каноническим уравнением параболы, 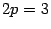, 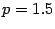. Осью параболы служит ось 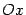, вершина находится в начале координат, ветви параболы направлены вдоль оси 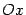. Для построения найдем несколько точек параболы. Для этого придаем значения переменному 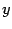и находим значения 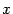. Возьмем точки 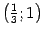, , 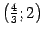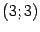. Учитывая симметрию относительно оси 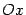, рисуем кривую (рис. 12.17)

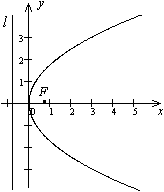
Рис.12.17.Парабола, заданная уравнением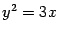

Фокус 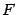лежит на оси 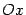на расстоянии 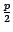от вершины, то есть имеет координаты 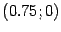. Директриса 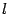имеет уравнение 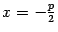, то есть .

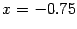Парабола так же, как и эллипс, обладает свойством, связанным с отражением света (рис. 12.18). Свойство сформулируем опять без доказательства.

Предложение 12.5 Пусть 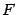-- фокус параболы, 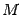-- произвольная точка параболы, 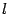-- луч с началом в точке 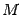параллельный оси параболы. Тогда нормаль к параболе в точке 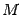делит угол, образованный отрезком 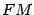и лучом 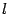, пополам.

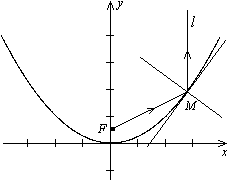
Рис.12.18.Отражение светового луча от параболы

Это свойство означает, что луч света, вышедший из фокуса 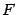, отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала.