Уравнение прямой на плоскости

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно, т.е. А² + В² ¹ 0. Это уравнение первого порядка называют общим уравнением прямой.

В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

- C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат

- А = 0, В ¹ 0, С ¹ 0 { By + C = 0}- прямая параллельна оси Ох

- В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – прямая параллельна оси Оу

- В = С = 0, А ¹ 0 – прямая совпадает с осью Оу

- А = С = 0, В ¹ 0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

12)Линии второго порядка

Линии второго порядка

Линии второго порядка, плоские линии, декартовы прямоугольные координаты которых удовлетворяют алгебраическому уравнению 2-й степени

a₁₁x² + a₁₂xy + a₂₂y² + 2a₁₃x + 2a₂₃y + a₁₁ = 0. (*)

Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к одному из 9 приведённых ниже канонических видов, каждому из которых соответствует определённый класс линий. Именно,

нераспадающиеся линии:

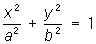— эллипсы,

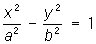— гиперболы,

y² = 2px — параболы,

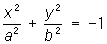— мнимые эллипсы;

распадающиеся линии:

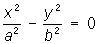— пары пересекающихся прямых,

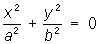— пары мнимых пересекающихся прямых,

x² - а² = 0 — пары параллельных прямых,

x² + а² = 0 — пары мнимых параллельных прямых,

x² = 0 — пары совпадающих параллельных прямых.

Исследование вида Л. в. п. может быть проведено без приведения общего уравнения к каноническому виду. Это достигается совместным рассмотрением значений т. н. основных инвариантов Л. в. п. — выражений, составленных из коэффициентов уравнения (*), значения которых не меняются при параллельном переносе и повороте системы координат:

, ,

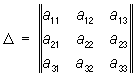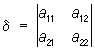S = a₁₁ + a₂₂, (a_ij = a_ji).

Так, например, эллипсы, как нераспадающиеся линии, характеризуются тем, что для них D ¹ 0; положительное значение инварианта d выделяет эллипсы среди других типов нераспадающихся линий (для гипербол d < 0, для парабол d = 0). Различить случаи действительного или мнимого эллипсов позволяет сопоставление знаков инвариантов D и S: если D и S разных знаков, эллипс действительный; эллипс мнимый, если D и S одного знака.

Три основные инварианта D, d и S определяют Л. в. п. (кроме случая параллельных прямых) с точностью до движения евклидовой плоскости: если соответствующие инварианты D, d и S двух линий равны, то такие линии могут быть совмещены движением. Иными словами, эти линии эквивалентны по отношению к группе движений плоскости (метрически эквивалентны).

Существуют классификации Л. в. п. с точки зрения др. групп преобразований. Так, относительно более общей, чем группа движений, — группы аффинных преобразований — эквивалентными являются любые две линии, определяемые уравнениями одного канонического вида. Например, две подобные Л. в. п. (см. Подобие)считаются эквивалентными. Связи между различными аффинными классами Л. в. п. позволяет установить классификация с точки зрения проективной геометрии, в которой бесконечно удалённые элементы не играют особой роли. Действительные нераспадающиеся Л. в. п.: эллипсы, гиперболы и параболы образуют один проективный класс — класс действительных овальных линий (овалов). Действительная овальная линия является эллипсом, гиперболой или параболой в зависимости от того, как она расположена относительно бесконечно удалённой прямой: эллипс пересекает несобственную прямую в двух мнимых точках, гипербола — в двух различных действительных точках, парабола касается несобственной прямой; существуют проективные преобразования, переводящие эти линии одна в другую. Имеется всего 5 проективных классов эквивалентности Л. в. п. Именно,

невырождающиеся линии

(x₁, x₂, x₃ — однородные координаты):

x₁² + x₂² — x₃² = 0 — действительный овал,

x₁² + x₂² + x₃² = 0 — мнимый овал,

вырождающиеся линии:

x₁² — x₂² = 0 — пара действительных прямых,

x₁² + x₂² = 0 — пара мнимых прямых,

x₁² = 0 — пара совпадающих действительных прямых.

13)Ф-ия. Способы задание ф-ии. Область определения и

область значения

Определение:

Николай Лобачевский 1834		Общее понятие требует, чтобы функцией от х называть число, которое дается для каждого х и вместе с каждым х постепенно изменяется
П.Лжен-Дирихле 1837		У есть функция переменной х (на отрезке а<=x<=b) , если каждому значению х (на этом отрезке) соответствует совершенно определенное значение у, причем безразлично, каким образом установлено это соответствие – аналитической формулой, графиком, таблицей либо даже просто словами

Область определения функции — множество, на котором задаётся функция.
Область значений функции — множество, которое получается в результате применения функции.

Способы задания функции:

• Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
• Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
• Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
• Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Монотонная функция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.(Пример:y=kx+b)

Нечётные и чётные функции — функции, графики которых обладают симметрией относительно изменения знака аргумента.

• Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).(Пример:y=1/x, y=x^3, y=sin x, y=tg x, y=ctg x, y=arcsin x, y=arctg x)
• Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).(Пример:y=|x|, y=x^2, y=cos x)

Периодическая функция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода).(Пример:Все тригонометрические функции)

Наименьшим положительным периодом функции называется такое число T, что T - период f, и ни одно положительное число, меньшее T, периодом f уже не является.

14)Основные характеристики ф-ий

Основные свойства функции.

1. Четность и нечетность

Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)

График четной функции симметричен относительно оси 0y

Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)

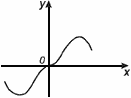
График нечетной функции симметричен относительно начала координат.

2.Периодичность

Функция f(x) называется периодической с периодом 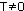, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

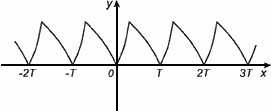
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

3. Монотонность (возрастание, убывание)

Функция f(x) возрастает на множестве Р , если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁)< f(x₂).

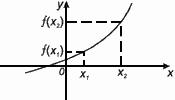
Функция f(x) убывает на множестве Р , если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁) > f(x₂).

4. Экстремумы

Точка Х_max называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Х_max , выполнено неравенство f(х) 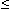f(X_max).

Значение Y_max=f(X_max) называется максимумом этой функции.

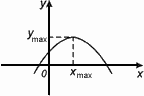
Х_max – точка максимума
У_max – максимум

Точка Х_min называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Х_min , выполнено неравенство f(х) 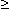f(X_min).

Значение Y_min=f(X_min) называется минимумом этой функции.

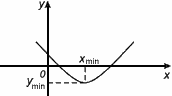
X_min – точка минимума
Y_min – минимум

X_min, Х_max – точки экстремума
Y_min, У_max – экстремумы.

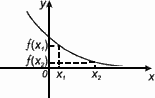
5. Нули функции

Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

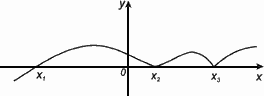
Х₁,Х₂,Х₃ – нули функции y = f(x).

15)Последовательность и ее св-ва

Задание числовой последовательности

Определение. Занумерованный ряд чисел a₁, a₂, a₃, …, a_n, … называется числовой последовательностью.

Наиболее простой способ задания последовательности – это ее задание с помощью формулы общего члена, т. е. формулы, явно выражающей зависимость n-ого члена последовательности от n.
Например, формула a_n = 2n задает последовательность четных чисел 2, 4, 6, 8, … .
Другим важным способом задания последовательности является так называемый рекуррентный способ, при котором задается выражение, связывающее n-ый член последовательности с одним или несколькими предыдущими. Слово рекуррентный происходит от латинского слова рекурсия, что означает возврат. Вычисляя новый, очередной член последовательности, мы как бы возвращаемся назад, к уже вычисленным, предыдущим членам.

Примеры
1. Рекуррентное соотношение a_n = a_{n – 1} + 2 вместе с условием a₁ = 1 задает арифметическую прогрессию с первым членом 1 и разностью 2: 1, 3, 5, 7, … . Это последовательность нечетных чисел.
2. Рекуррентное соотношение a_n = 2a_{n – 1} вместе с условием a₁ = 1 задает геометрическую прогрессию с первым членом 1 и знаменателем 2: 1, 2, 2², 2³, … . Это последовательность степеней двойки, начиная с нулевой степени.
Кстати, иногда члены последовательности удобно нумеровать с нуля, или вообще выбирать другой способ нумерации.
3. Рекуррентное соотношение a_n = a_{n – 1} + a_{n – 2} вместе с условием a₀ = 0, a₁ = 1 задает последовательность чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, … .

Последовательность может быть задана словесным описанием, в котором определяется процесс построения членов последовательности.
Например, описание «пусть a_n – это n-ое простое число» задает последовательность 2, 3, 5, 7, 11, 13, …, члены которой берутся из таблицы простых чисел или вычисляются каким-либо другим способом (например, с помощью решета Эратосфена).
Последовательность является дискретным вариантом понятия функции. В отличие от привычной функции типа y = f(x), аргумент которой x определен на некотором числовом промежутке, последовательность а₁, а₂, …, … можно считать функцией, аргумент которой n принимает дискретный ряд значений n = 1, 2, 3, … . Часто ее n-ый член можно выразить как значение некоторой обычной функции y = f(x) для x = n: a_n = f(n).

Начало формы   a0   d     an =   +   • n       a = Конец формы

Начало формы an =   • an-1 +   a0 =       a = Конец формы

Упражнение. Используя инструмент, выполните следующие задания.

1. Постройте явное (динамическая модель слева) и рекуррентное (динамическая модель справа) описание последовательности 1, 2, 3, 4, 5, ....

2. Постройте явное и рекуррентное описание последовательности -3, -1, 1, 3, 5, ....

3. Постройте рекуррентное описание последовательности 1, 2, 4, 8, 16, ....

4. Постройте рекуррентное описание последовательности 1, 2, 5, 14, 41, ....