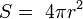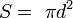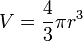Все линейные углы двугранного угла равны между собой.

24. Понятие многогранника, элементы многогранника. Понятие правильного многогранника

• Многогранником в трехмерном пространстве называется совокупность конечного числа плоских многоугольников такая, что

• каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым по этой стороне;

• от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя по очереди от одного многоугольника к другому, смежному с ним.

• Многоугольники, из которых состоят многогранники, называются гранями, их стороны – ребрами, а их вершины – вершинами многогранника.

Правильный многогранник или платоново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.

25. Понятие призмы. Боковая и полная поверхности прямой и наклонной призмы.

Призма— многогранник, две грани которого являютсяконгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани — параллелограммы.

Боковой поверхностью призмы называется объединение всех граней.

Полной поверхностью называется объединение всех граней и оснований призмы.

§ Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

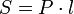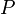§ Площадь боковой поверхности произвольной призмы , где — периметр перпендикулярного сечения, 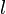— длина бокового ребра.

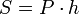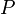§ Площадь боковой поверхности правильной призмы , где — периметр основания призмы, , 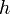— высота призмы.

26. Параллелепипед и его свойства. Куб.

Параллелепи́пед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм.

Свойства:

• Параллелепипед симметричен относительно середины его диагонали.
• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
• Противолежащие грани параллелепипеда параллельны и равны.
• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.

Свойства:

• Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям.
• В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным.
• В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
• Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
• В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.

Диагональю куба называют отрезок, соединяющий две вершины, симметричные относительно центра куба. Диагональ куба находится по формуле 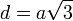, где d — диагональ, а — ребро куба.

27. Понятие пирамиды. Боковая и полная поверхности пирамиды.

Пирами́да — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса.

Боковая поверхность — это сумма площадей боковых граней:

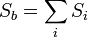
Полная поверхность — это сумма боковой поверхности и площади основания:

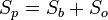
Для нахождения боковой поверхности в правильной пирамиде можно использовать формулы:

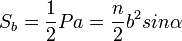
где 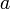— апофема , 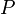— периметр основания, 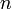— число сторон основания, 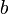— боковое ребро, 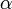— плоский угол при вершине пирамиды.

28. Понятие усеченной пирамиды. Боковая и полная поверхности усечённой пирамиды.

Усечё́ннаяпирами́да — многогранник, образованный пирамидой и её сечением, параллельным основанию.

Площадь боковой поверхности 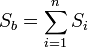равна сумме площадей боковых граней усечённой пирамиды.

Правильная усечённая пирамида — многогранник, образованный правильной пирамидой и её сечением, параллельным основанию.

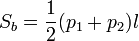§ (Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы)

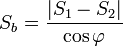§ , где 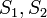— площади оснований, а 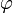— двугранный угол при основании пирамиды.

29. Цилиндрическая поверхность. Цилиндр. Круглый прямой цилиндр.

Цилиндрическая поверхность — поверхность, образуемая движением прямой (в каждом своём положении называемой образующей) вдоль кривой (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению.

Цили́ндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями, это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей.

В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.

Площадь боковой поверхности прямого кругового цилиндра:

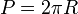, и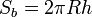

Площадь полной поверхности прямого кругового цилиндра:

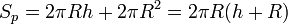
30. Коническая поверхность. Конус.

КОНИЧЕСКАЯ ПОВЕРХНОСТЬ - множество прямых (образующих), проходящих через данную точку (вершину конической поверхности) и пересекающих данную кривую (направляющую). Если направляющая - окружность, а вершина конической поверхности лежит на перпендикуляре (оси конической поверхности) к плоскости окружности, проходящем через ее центр, то коническая поверхность называется круглым конусом; он состоит из двух полостей, соединяющихся в его вершине.

Ко́нус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

31. Круглый прямой конус. Усечённый конус.

• Круговой конус — конус, основание которого является кругом.
• Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).

Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям

32. Шар, объем шара.

Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой.

Площадь поверхности 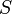и объём 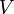шара радиуса определяются формулами:

• 

• 

• 

33. Сфера. Площадь сферы. Касательная и секущая плоскости к сфере.

Сфе́ра — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы.

Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра.

Площадь сферы

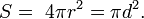
Площадь сегмента сферы

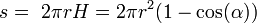, где H — высота сегмента, а 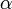— зенитный угол

Касательная плоскость к сфере (шару) определяется либо как плоскость, проходящая через точку на сфере перпендикулярно радиусу, проведенному в эту точку, либо как плоскость, имеющая со сферой (шаром) единственную общую точку.

34. Шаровой сегмент, шаровой сектор.

Шаровый сегмент -часть шара, отсекаемая какой-нибудь плоскостью.

Объём Ш. с.:

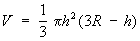
S =2πRh,

где R — радиус шара, h — высота Ш. с.

Шаровой секторполучается из шарового сегмента и конуса.

Объём шарового сектора: 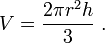, где r — радиус сектора, h — проекция хорды, стягивающей дугу сектора, на ось вращения.

.