Деревья и остовы. Остовы кратчайших маршрутов.

Дерево – связный граф, не содержащий циклов.

Лес (ациклический граф) – произвольный граф, не содержащий циклов. Компонентами леса являются деревья.

Теорема о дереве (5 различных определений дерева).

1. Граф G – дерево, связный ацикличный граф.

2. Любые две несовпадающие вершины графа G соединены единственной простой цепью.

3. Граф G связен и количество ребер в нем на 1 меньше, чем количество вершин.

4. Граф G ацикличен: q=p-1, p=q+1.

5. Граф G ацикличен, и если любую пару его несовпадающих несмежных вершин соединить ребром е, то полученный граф G+e будет содержать ровно один цикл.

Теорема о висячих вершинах дерева. В любом нетривиальном (p³2) дереве имеется, по крайней мере, 2 висячие вершины.

Теорема о центре дерева. Центр любого дерева состоит либо из 1, либо из 2 смежных вершин.

Двоичные деревья (b – деревья)– это деревья, у которых степени любых не концевых вершин равны 2.

Способы обхода деревьев

1. Способ обхода в глубинуПоиск в глубину подразумевает просмотр ветвей дерева.

2. Способ обхода в ширинуПодразумевает просмотр вершин по ярусам в иерархическом представлении. Здесь под использованием вершины подразумевается просмотр всех «соседей» данной вершины.

Остов (каркас, скелет) графа G – это остовный подграф графа G, задающий дерево на каждой компоненте связности графа G.

Для связного графа остов – это дерево, покрывающее все вершины исходного графа. Очевидно, что в каждом графе существует остов, в общем случае не один. Его можно получить, разрушая циклы в каждой компоненте связности.

Ребра остова Т некоторого графа G называются ветвями, а ребра графа G, не вошедшие в остов называются хордами.

Алгоритмы поиска остовов кратчайших маршрутов

Имеется граф, заданный матрицей весов, т.е. существует G = (V,E), C = ||C_ij||, i, j = 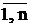, где C_ij - вес ребра, если оно существует. Требуется найти остов с минимальным суммарным весом ребер.

Алгоритм Краскала

Выбирается произвольная вершина графа G.

Упорядочиваем ребра в порядке не убывания их весов.

На каждом шаге пустому графу Ор, где р - количество вершин исходного графа, добавляется ребро с min весом из списка. Добавляемое ребро не должно приводить к образованию цикла. Алгоритм заканчивает работу, если количество ребер в формируемом графе станет равным р – 1.

Алгоритм Прима

Отличается от алгоритма Краскала тем, что на каждом шаге строится не просто граф без циклов, но дерево.

Упорядочиваем ребра исходного графа в порядке не убывания. Строим пустой граф Ор, где р - количество вершин исходного графа.

На каждом шаге в граф Ор добавляем ребро из списка ребер, чтобы не образовался цикл и не должно нарушать связность. Для этого список ребер каждый раз просматривается, начиная с I ребра, и алгоритм начинает остов кратчайших маршрутов посредством разрастания поддерева T с одной вершиной. Поддерево T постепенно разрастается за счет присоединения ребер (x_i, x_j), где вершина x_i Î текущему дереву, а x_j - ему не принадлежит и вес ребра (x_j, x_i) наименьший из всех возможных.

Эйлера и гамильтонов графы.

Эйлеров цикл –цикл, содержащий все рёбра исходного графа (каждое ребро используется ровно 1 раз).

Эйлеров граф– связный граф,содержащий эйлеров цикл.

Теорема Эйлераили критерий существования в графе эйлерового цикла:

Связный граф G является эйлеровым тогда и только тогда,

когда степени всех его вершин четны

Следствие №1. Для связного графа G множество ребер можно разбить на простые циклы, если граф эйлеров.

Следствие №2. Для того чтобы связный граф G покрывался единственной эйлеровой цепью, необходимо и достаточно, чтобы он содержал ровно 2 вершины с нечетной степенью. Тогда цепь начинается в одной из этих вершин и заканчивается в другой.

Эйлерова цепь – цепь с концевыми вершинами (a, b), начинающаяся в вершине a, заканчивающаяся в вершине b и содержащая каждое ребро исходного графа ровно 1 раз.

Гамильтонов цикл – простой цикл, содержащий каждую вершину графа.

Гамильтонов граф– граф, содержащий гамильтонов цикл.

Достаточные условиясуществования гамильтонова цикла в графе

Теорема Дирака

Если число вершин графа p ³ 3 и для любой вершины выполняется условие

" v_i, i = 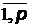; deg v_i ³ 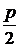, то граф G – гамильтонов

Теорема Оре

Если число вершин графа p ³ 3 и для любых двух несмежных вершин u и v выполняется неравенство:

deg u + deg v ³ p, то граф G – гамильтонов

9. Плоские и планарные графы.

Плоским - называется такой граф G у которого, вершины - точки плоскости, а ребра - непрерывные плоские линии без пересечений и самопересечений, причем соединяющие вершины так, что никакие два ребра не имеют общих точек, кроме инцидентных им обоим вершин.

Планарный - это граф, который изоморфен плоскому.

О планарных графах говорят, что они имеют плоскую укладку.

Жорданова кривая- это непрерывная спрямляемая линия, не имеющая самопересечений.

Гранью плоского графа называется максимальное по включению количество точек плоскости, каждая пара которых может быть соединена Жордановой кривой, не пересекающей ребра графа.

Граница грани - это множество вершин и ребер, принадлежащих грани.