Булевы функции. Булева алгебра.

Пусть множество Х состоит из двух элементов 0 и 1, Х={0,1};множество Y=Xⁿ = {(x1, …,xn) | "i = 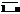, xi Î X}.

Логическая переменная – это переменная, которая может принимать только два значения: истина или ложь (true/false, 1/0).

Функция алгебры логики (булева функция) – f(x1,x2, …,xn) – это функция, у которой все аргументы есть логические переменные, и сама функция принимает только логические значения.

Количество всевозможных, различных двоичных наборов длиной n равно 2ⁿ.

способы описания ФАЛ:

Табличный (Любую булеву функцию можно представить таблицей, имеющей 2n строк. Такая таблица называется таблицей истинности.)

Графический (ФАЛ можно представить в виде n-мерного единичного куба: если наборам значений аргументов сопоставить точки n-мерного пространства, то множество 2n наборов определяет множество вершин n-мерного куба.)

- аналитический

- словесный

Законы булевой алгебры

Коммутативность

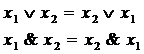
Ассоциативность

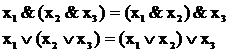
Дистрибутивность

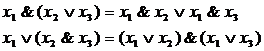
Законы де Моргана

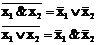
Законы поглощения

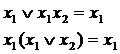
Законы склеивания

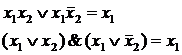
7)

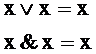
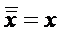
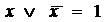
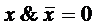
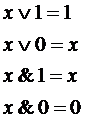
Теория неориентированных графов. Подграф и изоморфизм.

Пусть V – некоторое непустое множество (V ¹ Æ).

V⁽²⁾ – множество всех его двухэлементных подмножеств (V⁽²⁾={(u,v)|u,vÎV,неупорядоченная пара}).

Неориентированный граф G – пара множеств (V,E), E Í V⁽²⁾ ,

где V – множество вершин графа G,

E – множестворёбер графа G.

Если |V|=p, а |E|=q, то обозначают граф G – (p, q)- граф или p-граф.

Изоморфные графы – существует взаимноодназначное соответствие, т. е. биекция, между множествами их вершин, сохраняющая отношение смежности.

Изоморфизм графов G и H : G @ H.

Изоморфизм есть отношение эквивалентности, т. к. он:

- симметричен;

- рефлексивен;

- транзитивен.

Подграф G₁ = (V₁, E₁) графа G = (V, E) –граф, у которого все вершины и ребра удовлетворяют следующим соотношениям V₁ Í V, E₁ Í E.

Остовный подграф графа G -подграф, содержащийвсе вершины графа G, множество ребер есть подмножество ребер графаG.

Порожденный подграф ( порожденный подмножеством вершин V₁) – подграф, множество вершин которого V₁ Í V,а множество реберЕ₁ содержит все ребра графа G, инцидентные выбранным вершинам V₁.

Например:

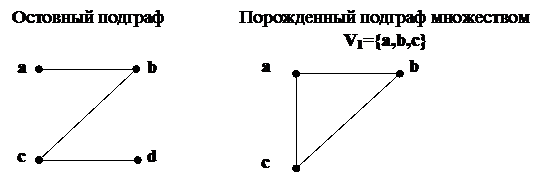Связность в неорграфах.

Связный неориентированный граф G – любая пара вершин соединена маршрутом (простой цепью) в G.

Компонента связности или компонента графа G – максимальный связный подграф графа G.

Любой несвязный граф содержит, по крайней мере, две компоненты связности.

Теорема 1: Любой граф G является объединением своих компонент связности.

Теорема 2: Либо граф, либо его дополнение связны.

Число вершинной связности χ(G) –наименьшее число вершин, удаление которых приводит к несвязному или одновершинному графу.

Число реберной связности l(G) –наименьшее число рёбер, удаление которых приводит к несвязному или одновершинному графу.

Например:

Граф G: ГрафR:

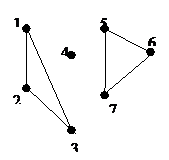
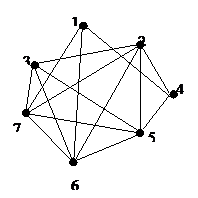
Граф G– связен.

Граф R – несвязен, в графе R три компоненты связности, R₁ = {1,2,3}, R2 ={4}, R3={5,6,7}.