Основы дискретной математики (Назарова И.А.)
Основы дискретной математики (Назарова И.А.)
Множество. Операции над множествами. Алгебра множеств.
Множество– объединение в одно целое различимых между собой элементов.
Конечное множество – множество, состоящее из конечного числа элементов.
Бесконечное множество – множество, состоящее из бесконечного числа элементов.
Пустое множество – множество, не содержащее ни одного элемента -
Универсальное –множество, содержащее все возможные элементы.
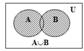 Операции над множествами
Операции над множествами
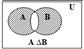
1) Объединение множеств A и B (A È B) – множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.
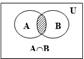 2) Пересечениемножеств A и B (AB) – множество, состоящее из всех элементов, принадлежащих каждому из этих множеств.
2) Пересечениемножеств A и B (AB) – множество, состоящее из всех элементов, принадлежащих каждому из этих множеств.
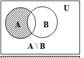 3) Разность множеств A и B (A \ B) – множество, состоящее из всех элементов множества A , не принадлежащих множеству B.
3) Разность множеств A и B (A \ B) – множество, состоящее из всех элементов множества A , не принадлежащих множеству B.
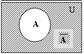 4) Дополнениемножества A в универсальном множестве U (
4) Дополнениемножества A в универсальном множестве U ( 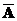 , ØA) – множество, состоящее из всех элементов универсального множества U, не принадлежащих множеству A.
, ØA) – множество, состоящее из всех элементов универсального множества U, не принадлежащих множеству A.
 5) Симметрическая разность множеств A и B (AÅB или ADB) – множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств.A D B = (A \ B) È (B \ A) = (A È B) \ (A Ç B)
5) Симметрическая разность множеств A и B (AÅB или ADB) – множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств.A D B = (A \ B) È (B \ A) = (A È B) \ (A Ç B)
Основные законы алгебры множеств
1) коммутативные законы
А È В = В È А
А Ç В = В Ç А
А D В = В D А
2) ассоциативные законы
А È (В È С) = (А È В) È С
А Ç (В Ç С) = (А Ç В) Ç С
3) дистрибутивные законы
А È (В Ç С) = (А È В) Ç (А È С)
А Ç (В È С) = (А Ç В) È (А Ç С)
4) законы с Æ и u
А È Æ = А А Ç U = А А È  = U
= U
А Ç Æ = Æ А È U = U А Ç 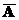 = Æ
= Æ
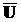 = Æ
= Æ 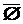 = U
= U
6) законы идемпотентности
А Ç А = А А È А = А 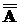 = А
= А
7) законы поглощения
А È (А Ç В) = А
А È ( 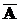 Ç В) = А È В
Ç В) = А È В
А Ç (А È В) = А
А Ç ( 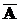 È В) = А Ç В
È В) = А Ç В
8) законы Де Моргана
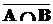 =
= 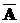 È
È 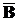
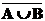 =
= 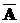 Ç
Ç 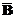
9) законы склеивания
(А Ç В) È ( 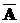 Ç В) = В
Ç В) = В
(А È В) Ç ( 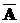 È В) = В
È В) = В
Бинарные отношения и их свойства.
Бинарное отношение на множествах X и Y – произвольное подмножество прямого произведения двух множеств r Í Х x Y = {(x,y) | xÎX, yÎY}.
Если (x,y)Îr,то (x,y) находятся в отношении rили связаны отношением r:
х r y или y = r(х)
Область определения Drбинарного отношения - множество первых элементов каждой упорядоченной пары. Dr = {x | (x,y) Î r}
Область значений Jrбинарного отношения - множество вторых элементов каждой упорядоченной пары. J r = {y | (x, y) Î r}.
Способы задания отношений
Список пар
Характеристическая функция
Графическое изображение
Матрица отношения
Свойства бинарных отношений
Пусть rзадано на множестве X, r Í Х2
1) рефлексивность:" х Î Х х r х.
2) антирефлексивность:± х Î Х х r х.
3) нерефлексивность:$ х Î Х (x, x) Ï r.
4) симметричность:" х, y Î Х х r y => y r х.
5) антисимметричность:" х, y Î Х х r y, y r х Ûx = y.
6) транзитивность:" х, y, z Î Х х r y, y r z => x r z.
Отношение порядка – антисимметрично, транзитивно.
Отношение нестрого порядка ( 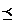 ) - рефлексивно,
) - рефлексивно,
антисимметрично,
транзитивно.
Отношениестрогого порядка ( 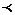 ) - антирефлексивно,
) - антирефлексивно,
антисимметрично,
транзитивно.
В отношениях полного порядка все элементы сравнимы между собой, а в отношениях частичного порядка не все элементы сравнимы между собой.
Отношение эквивалентности ( ~ )- рефлексивно,
симметрично,
транзитивно .
Класс эквивалентности для х : [ x ] = { yÎ Х | x ~ y}
Обратное отношение получается путём перестановки значений в парах исходного отношения.
Композиция отношений r иg -отношение, состоящее из пар
r○g={(x, z)| х r у, y g z }
3. Основные комбинаторные соединения (перестановки, сочетания и размещения с повторением и без повторений элементов).
Формулы пересчета для основных видов комбинаторных соединений
| Соединения | Без повторений элементов | С повторениями элементов |
| Сочетания | 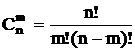 | 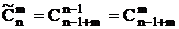 |
| Размещения | 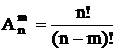 | 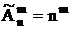 |
| Перестановки | 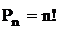 | 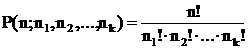 |
Соединения без повторений
Соединения – простые комбинаторные объекты, к которым относятся перестановки, сочетания и размещения.
1 Перестановка из n элементов – упорядоченная последовательность элементов n-элементного множества (кортеж).
Различные перестановки отличаются только порядком элементов в них.
Число перестановокизnразличных элементов равно: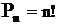
2 Размещения – упорядоченная последовательность из m элементов множества, содержащего всего n элементов.
Различные размещения отличаются составом элементов и (или) порядком их следования.
Число размещенийизnразличных элементов поmравно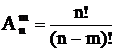
3 Сочетания из n по m – последовательность из m элементов, взятых из n-элементного множества, без учета порядка следования элементов.
Сочетание– произвольное (неупорядоченное) m-подмножество из n элементов.
Различные сочетания отличаются составом элементов, но не их порядком.
Числосочетанийизnразличных элементов поmравно: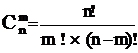 ,m ≤ n.
,m ≤ n.
Свойства сочетаний
1) 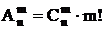 Þ
Þ 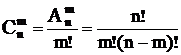 ;
;
2) 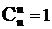 ;
; 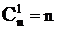 ;
; 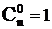 ;
; 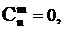 при m £ 0 и m ³n .
при m £ 0 и m ³n .
3) Симметричность числа сочетаний: 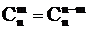 .
.
4) Правило Паскаля. Для числа сочетаний из n по m справедливо следующее рекуррентное соотношение: 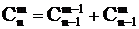 .
.
5) Бином Ньютона.
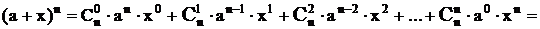
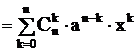
.
При a = x = 1, 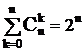 ,
, 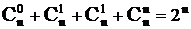 ,где
,где 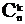 , k = 0,1… n - биномиальные коэффициенты.
, k = 0,1… n - биномиальные коэффициенты.
Соединения с повторениями
Пусть дано множество А, состоящее из n элементов, в котором n1 элементов принадлежит первому типу; n2 элементов принадлежит второму типу элементов, nk - k-тому типу. Элементы одного и того же типа неразличимы между собой.
Спецификацией множества А называется набор (n1, n2, … ,nk).
Следствие:
Если множество А, | А | = n, состоит из объектов 2 типов: m-одного типа, (n – m) –другого: 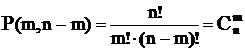
Число перестановок с повторениями n - элементного множества с
заданной спецификацией равно
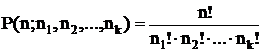 , где
, где 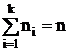 .
.
В общем случае:
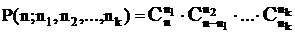 .
.
Размещения с повторениями
(m перестановки с неограниченными повторениями)
Пусть А = {a1, a2,…, an} , где a1, a2,…, an – “представители” 1-го, 2-го, … n-го типа элементов. Объектов каждого типа имеется в неограниченном количестве, элементы одного типа неразличимы между собой. Рассмотрим следующую схему выбора упорядоченной последовательности из m элементов: выбираем элемент на 1-е место, имеется n вариантов выбора. После этого элемент возвращается обратно и может быть выбран еще, т.е. на 2-е место имеется n претендентов и т.д. На m-е место также имеется n претендентов.
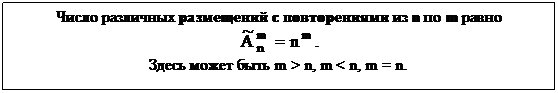 |
Сочетания с повторениями
Пусть А = {a1, a2,…, an}, где a1, a2,…, an - “представители” 1-го, 2-го, …, n-го типа элементов. Объектов каждого типа имеется в неограниченном количестве, элементы одного типа неразличимы между собой.
Сочетания с повторениями отличаются составом элементов, входящих в выбираемое множество. Порядок элементов не имеет значения. Имеет значение, сколько элементов каждого типа вошло в сочетание.
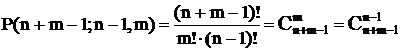
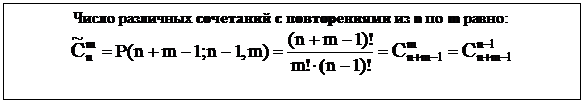
Законы булевой алгебры
Коммутативность
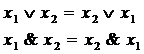
Ассоциативность
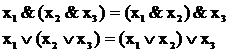
Дистрибутивность
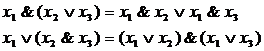
Законы де Моргана
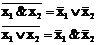
Законы поглощения
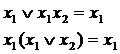
Законы склеивания
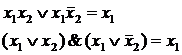
7)
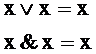
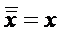
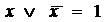
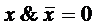
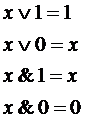
Связность в неорграфах.
Способы обхода деревьев
1. Способ обхода в глубинуПоиск в глубину подразумевает просмотр ветвей дерева.
2. Способ обхода в ширинуПодразумевает просмотр вершин по ярусам в иерархическом представлении. Здесь под использованием вершины подразумевается просмотр всех «соседей» данной вершины.
Для связного графа остов – это дерево, покрывающее все вершины исходного графа. Очевидно, что в каждом графе существует остов, в общем случае не один. Его можно получить, разрушая циклы в каждой компоненте связности.
Ребра остова Т некоторого графа G называются ветвями, а ребра графа G, не вошедшие в остов называются хордами.
Алгоритмы поиска остовов кратчайших маршрутов
Имеется граф, заданный матрицей весов, т.е. существует G = (V,E), C = ||Cij||, i, j = 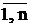 , где Cij - вес ребра, если оно существует. Требуется найти остов с минимальным суммарным весом ребер.
, где Cij - вес ребра, если оно существует. Требуется найти остов с минимальным суммарным весом ребер.
Алгоритм Краскала
Выбирается произвольная вершина графа G.
Упорядочиваем ребра в порядке не убывания их весов.
На каждом шаге пустому графу Ор, где р - количество вершин исходного графа, добавляется ребро с min весом из списка. Добавляемое ребро не должно приводить к образованию цикла. Алгоритм заканчивает работу, если количество ребер в формируемом графе станет равным р – 1.
Алгоритм Прима
Отличается от алгоритма Краскала тем, что на каждом шаге строится не просто граф без циклов, но дерево.
Упорядочиваем ребра исходного графа в порядке не убывания. Строим пустой граф Ор, где р - количество вершин исходного графа.
На каждом шаге в граф Ор добавляем ребро из списка ребер, чтобы не образовался цикл и не должно нарушать связность. Для этого список ребер каждый раз просматривается, начиная с I ребра, и алгоритм начинает остов кратчайших маршрутов посредством разрастания поддерева T с одной вершиной. Поддерево T постепенно разрастается за счет присоединения ребер (xi, xj), где вершина xi Î текущему дереву, а xj - ему не принадлежит и вес ребра (xj, xi) наименьший из всех возможных.
Эйлера и гамильтонов графы.
Эйлеров цикл –цикл, содержащий все рёбра исходного графа (каждое ребро используется ровно 1 раз).
Эйлеров граф– связный граф,содержащий эйлеров цикл.
Теорема Эйлераили критерий существования в графе эйлерового цикла:
Связный граф G является эйлеровым тогда и только тогда,
когда степени всех его вершин четны
Следствие №1. Для связного графа G множество ребер можно разбить на простые циклы, если граф эйлеров.
Следствие №2. Для того чтобы связный граф G покрывался единственной эйлеровой цепью, необходимо и достаточно, чтобы он содержал ровно 2 вершины с нечетной степенью. Тогда цепь начинается в одной из этих вершин и заканчивается в другой.
Эйлерова цепь – цепь с концевыми вершинами (a, b), начинающаяся в вершине a, заканчивающаяся в вершине b и содержащая каждое ребро исходного графа ровно 1 раз.
Гамильтонов цикл – простой цикл, содержащий каждую вершину графа.
Гамильтонов граф– граф, содержащий гамильтонов цикл.
Достаточные условиясуществования гамильтонова цикла в графе
Теорема Дирака
Если число вершин графа p ³ 3 и для любой вершины выполняется условие
" vi, i = 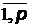 ; deg vi ³
; deg vi ³ 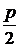 , то граф G – гамильтонов
, то граф G – гамильтонов
Теорема Оре
Если число вершин графа p ³ 3 и для любых двух несмежных вершин u и v выполняется неравенство:
deg u + deg v ³ p, то граф G – гамильтонов
9. Плоские и планарные графы.
Плоским - называется такой граф G у которого, вершины - точки плоскости, а ребра - непрерывные плоские линии без пересечений и самопересечений, причем соединяющие вершины так, что никакие два ребра не имеют общих точек, кроме инцидентных им обоим вершин.
Планарный - это граф, который изоморфен плоскому.
О планарных графах говорят, что они имеют плоскую укладку.
Жорданова кривая- это непрерывная спрямляемая линия, не имеющая самопересечений.
Гранью плоского графа называется максимальное по включению количество точек плоскости, каждая пара которых может быть соединена Жордановой кривой, не пересекающей ребра графа.
Граница грани - это множество вершин и ребер, принадлежащих грани.
Основы дискретной математики (Назарова И.А.)
