В деформируемом трещиноватом пласте

Полагаем, что однородная несжимаемая жидкость обладает неизменной вязкостью.

Определим конкретный вид потенциальной функции течения для однородной несжимаемой жидкости. На основании предположений в постановке задачи имеем:

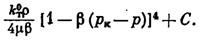
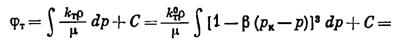(V.2)

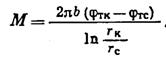Если поток плоско-радиальный (j= 1),

то массовый дебит можно подсчитать из: (V.2а)

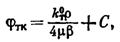В условиях данной задачи значение потенциальной функции на контуре питания ( ):

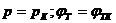(V.3)

а на стенке скважины потенциальная функция определяется из выражения:

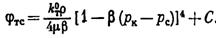(V.4)

Составляя разность (V.3) и (V.4) и подставляя в (V.2а) (У.2а) получаем:

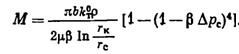(V.5)

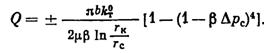Поделив (V.5) на плотность жидкости, получаем объёмный дебит скважины, эксплуатирующей трещиноватый пласт:

(V.6)

Заметим, что знаки перед выражением в правой части зависят от того, является ли скважина стоком или источником (нагнетательная скважина). При 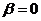, т. е. для недеформируемого трещиноватого пласта, после раскрытия неопределенности получаем формулу Дюпюи.

Распределение давления в деформируемом трещиноватом пласте можно получить, если известен вид формулы для распределения потенциальной функции течения в таком коллекторе.

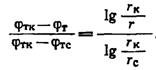Учитывая сказанное ранее в главе IV для плоско-радиального потока (см форм. IV.26), зависимость для определения потенциальной функции в любой точке деформируемого трещиноватого пласта можем представить в виде:

(V.7)

Здесь 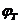определяется из (V.7), а разность 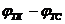— из выражений (V.3) и (V.4).

После подстановки в (V.7) значений 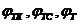получаем:

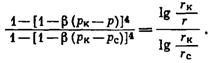(V.8)

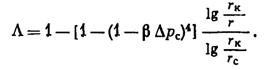Решая уравнение (V.8) относительно р — давления в любой точке деформируемого трещиноватого пласта, имеем:

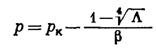,где (V.9)

Как видно, зависимость (V.9) в значительной степени отличается от соответствующего уравнения для определения давления в любой точке пористого коллектора:

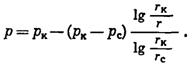(V.10)

Однако здесь следует указать на общность формулы (V.8) с (V.10), так как формула (V.10) может быть получена из (V.8) при следующих допущениях: 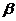весьма мало и депрессия на пласт 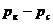относительно невелика.

Тогда:

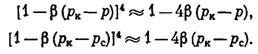
Из (V.8) прямо следует (V.10).

На рис. 15 приведены пьезометрические кривые для одиночно работающих скважин в деформируемом трещиноватом коллекторе

и в пористомпласте, построенные на основе выведенных зависимостей. Характер графиков подтверждает мысль о том, что в деформируемом трещиноватом пласте за счет уменьшения раскрытости трещин при снижении пластового давления возникают дополнительные фильтрационные сопротивления, вызывающие резкое понижение пьезометрического уровня на сравнительно небольшом расстоянии от скважины (в ближайшей к скважине зоне), причем при прочих равных условиях более резко снижается давление в пласте с большим значением .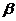

Рис. 15. Кривые распределения давления.

1 и 2 – для деформируемого трещиноватого коллектора; 3 – для пористого коллектора

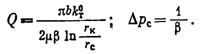
Большое практическое значение приведенной расчетной схемы для однородной несжимаемой жидкости состоит в том, что параметры трещиноватого пласта можно определять по индикаторным кривым, построенным на основе промысловых исследований. Из упомянутых параметров наибольшую ценность имеют проницаемость 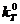и коэффициент 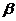. Из формулы для объемного дебита (V.6) следует, что индикаторная кривая, отвечающая этой зависимости, есть парабола четвертого порядка с координатами вершины:

(V.11)

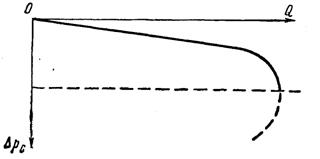
Рис. 16. Индикаторная кривая, построенная при фильтрации несжимаемой жидкости в трещиноватом пласте.

Парабола проходит через начало координат, симметрична относительно оси, параллельной оси дебитов; вторая ветвь параболы смысла не имеет (рис. 16).

Глава VI