Однородной несжимаемой жидкости
В этом и следующих параграфах мы будем применять общие дифференциальные уравнения одномерного потока, приведенные в §§ 4 и 5 этой главы, к особенностям той или иной жидкости или газа. Чтобы описывать картину движения и исследовать течение жидкости или газа в пласте с учетом их физических свойств, следует придерживаться такого порядка.
1. Находится уравнение состояния по формуле (IV.9) или по формулам (IV.28) и (IV.29) с помощью определенного физического закона, выражающего состояние рассматриваемой жидкости или газа.
2. Определяется функция состояния 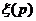 или
или 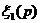 из уравнения состояния. Подставив
из уравнения состояния. Подставив 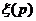 в формулу (IV.5), находят зависимость потенциальной функции
в формулу (IV.5), находят зависимость потенциальной функции 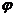 от давления
от давления 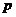 , если движение потенциальное; подставив
, если движение потенциальное; подставив 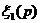 в формулу (IV.28) или (IV.33), находят зависимость вспомогательной функции
в формулу (IV.28) или (IV.33), находят зависимость вспомогательной функции 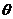 от давления, если фильтрация происходит по нелинейному закону.
от давления, если фильтрация происходит по нелинейному закону.
З. Устанавливается форма потока и определяется показатель формы j. Найденную  подставляют в формулы (IV.19), (IV.21), (IV.23) или (IV.20), (IV.24), (IV.26), если движение потенциальное;
подставляют в формулы (IV.19), (IV.21), (IV.23) или (IV.20), (IV.24), (IV.26), если движение потенциальное;  подставляют в формулу (IV.30) или (IV.34), если закон фильтрации нелинейный. Таким путем получают зависимость между давлением р и основной координатой
подставляют в формулу (IV.30) или (IV.34), если закон фильтрации нелинейный. Таким путем получают зависимость между давлением р и основной координатой 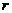 ; эта зависимость показывает распределение давления в пласте. График этой зависимости называют пьзометрической линией.
; эта зависимость показывает распределение давления в пласте. График этой зависимости называют пьзометрической линией.
4. Определяется массовый или объёмный дебит на основе граничных условий по формулам (IV.22) или (IV.25), если движение потенциальное, и по формуле (IV.31) или (IV.35) (, если закон фильтрации нелинейный. Зависимость между дебитом и разностью значений
 или
или 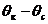 позволяет построить так называемую индикаторную линию, которая в нефтепромысловой практике есть графическое представление зависимости дебита от перепада давления
позволяет построить так называемую индикаторную линию, которая в нефтепромысловой практике есть графическое представление зависимости дебита от перепада давления 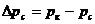 (
( 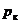 - давление на контуре питания пласта,
- давление на контуре питания пласта, 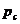 - давление на контуре стока).
- давление на контуре стока).
5. Определяется время движения частицы жидкости по прямолинейной траектории с учётом соотношения между скоростью 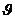 и средней скоростью движения
и средней скоростью движения 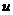 (
( 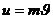 ); для этого замечаем, что
); для этого замечаем, что  . Далее используем формулы (IV.17)-(IV.18) или (IV.27), (IV.32). (Указанный ход исследования потока покажем на примере потенциального движения – практическое занятие).
. Далее используем формулы (IV.17)-(IV.18) или (IV.27), (IV.32). (Указанный ход исследования потока покажем на примере потенциального движения – практическое занятие).
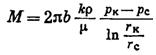 Для плоско-радиального потока массовый дебит подсчитывается по следующей формуле, полученной из формулы (IV.35):
Для плоско-радиального потока массовый дебит подсчитывается по следующей формуле, полученной из формулы (IV.35):
(IV.36)
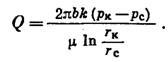 Разделяя равенство (IV.36) на плотность жидкости
Разделяя равенство (IV.36) на плотность жидкости  , получим объёмный дебит
, получим объёмный дебит 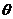 :
:
(IV.37)
Формулу (IV.37) принято называть формулой Дюпюи.
Введём следующее обозначение:
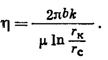 (IV.38)
(IV.38)
Представим теперь формулу (IV.37) так: 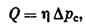 (IV.39)
(IV.39)
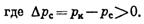
Рис. 13. Карта изобар для плоско-радиального потока
Зависимость между 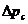 и
и 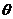 — линейная. Прямая, построенная в координатах
— линейная. Прямая, построенная в координатах 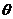 и
и 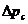 при помощи формулы (IV.39), — индикаторная линия.
при помощи формулы (IV.39), — индикаторная линия.
Величина  называется коэффициентом продуктивности.
называется коэффициентом продуктивности.
Легко понять, что 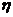 в данном случае численно равен тангенсу угла наклона прямой к оси перепадов
в данном случае численно равен тангенсу угла наклона прямой к оси перепадов 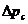 ;
; 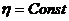
Массовая скорость фильтрации для простейшего одномерного потока определяется по формуле (IV.16).
В § 4 после формулы (IV.16) приводятся значения площади изобарической поверхности F, соответствующие каждому виду одномерного потока. Пользуясь этими значениями и формулой (IV.16), приходим к выводу, что при  для прямолинейно-параллельного потока скорость фильтрации
для прямолинейно-параллельного потока скорость фильтрации 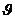 неизменна вдоль координаты
неизменна вдоль координаты 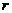 ; в плоско-радиальном потоке
; в плоско-радиальном потоке 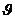 обратно пропорциональна расстоянию от оси скважин; в сферически-радиальном потоке
обратно пропорциональна расстоянию от оси скважин; в сферически-радиальном потоке 
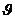 обратно пропорциональна квадрату расстояния от общего центра всех полусферических поверхностей — изобар.
обратно пропорциональна квадрату расстояния от общего центра всех полусферических поверхностей — изобар.
Найдём теперь время движения частицы жидкости вдоль координаты 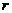 .
.
Скорость перемещения частицы жидкости вдоль координаты 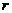
 (IV.40)
(IV.40)
Формула (IV.40) выражает величину некоторой средней скорости течения, взятой для площади (  ), нормальной к данному одномерному потоку. Определяя, согласно формуле (II.7), величину скорости фильтрации
), нормальной к данному одномерному потоку. Определяя, согласно формуле (II.7), величину скорости фильтрации 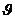 , для той же площади, найдем, что
, для той же площади, найдем, что
 (IV.41)
(IV.41)
Заметим, что левая часть формулы (IV.18) есть массовая скорость фильтрации. Разделяя её на  , получим величину скорости фильтрации в функции координаты
, получим величину скорости фильтрации в функции координаты 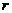 ; пользуясь затем формулой (IV.41), составим следующее дифференциальное уравнение:
; пользуясь затем формулой (IV.41), составим следующее дифференциальное уравнение:
 (IV.41)
(IV.41)
Значения А и j приведены в табл. 1.
Допустим, что движение частицы жидкости рассматривается между двумя точками пласта, имеющими координаты 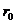 и
и 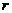 . Интегрируя уравнение (IV.41), получим формулу для подсчёта времени движения частицы t:
. Интегрируя уравнение (IV.41), получим формулу для подсчёта времени движения частицы t:
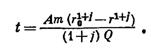 (IV.41)
(IV.41)
Если одна из координат ( 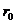 или
или 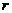 ) определяет радиус скважины или координату галереи, можно по формуле (IV.41) подсчитывать время отдачи или время поглощения жидкости пластом при поддержании постоянного дебита
) определяет радиус скважины или координату галереи, можно по формуле (IV.41) подсчитывать время отдачи или время поглощения жидкости пластом при поддержании постоянного дебита 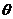 .
.
Для извлечения из пласта данного количества жидкости за определённый промежуток времени требуется поддерживать определённый дебит 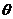 . Установление этого дебита связано с созданием такой депрессии
. Установление этого дебита связано с созданием такой депрессии 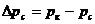 , которая обусловлена действующим при этом законом фильтрации и видом одномерного потока. Очевидно, что для несжимаемой жидкости с повышением депрессии
, которая обусловлена действующим при этом законом фильтрации и видом одномерного потока. Очевидно, что для несжимаемой жидкости с повышением депрессии 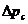 всегда повышается дебит — см. формулы (IV.36) и (IУ.37).
всегда повышается дебит — см. формулы (IV.36) и (IУ.37).
Можно принимать, что напорное движение несжимаемой жидкости в нефтеносном пласте происходит в случаях так называемого жесткого водонапорного режима пласта. В процессе разработки нефтяной залежи в условиях водонапорного режима доминирующей формой пластовой энергии является энергия воды, вытесняющей нефть к скважинам. При этом закачка воды через нагнетательные скважины или естественный приток краевой (контурной) воды компенсирует отбор жидкости из скважины.
