Значение и роль подземной гидравлики в развитии научных основ разработки нефтяных и газовых месторождений

Глава I

Значение и роль подземной гидравлики в развитии научных основ разработки нефтяных и газовых месторождений

Подземная гидравлика — наука о движении нефти, воды, газа и их смеси в пористых и трещиноватых горных породах, слагающих продуктивные пласты и массивы.

Поскольку подземная гидравлика изучает разновидность механического движения, её можно считать отделом механики и называть подземной гидрогазомеханикой.

Те или иные положения подземной гидравлики устанавливаются и развиваются строгими или упрощенными математическими методами на основе данных о движении жидкости и газа в реальных пластах.

Существуют естественные подземные потоки пластовой жидкости. Движение жидкости и газа в пластах возникает всякий раз, когда начинают добывать из залежи нефть и газ. Это движение обладает специфическими особенностями, отличающими его от движения жидкости и газа по трубам или в открытых руслах. Знать особенности их движения в пористой или трещиноватой среде необходимо для того, чтобы вести успешную разработку нефтяных и газовых место­рождений.

Процесс отдачи нефти и газа пластом сопровождается физико-химическими явлениями, возникающими в самом пласте. Так, если движение жидкости происходит по узким проходам (каналам или мелким трещинам), внутри горной породы возникают поверхностные явления, обусловленные взаимодействием между молекулами жидко­сти и твердого вещества на стенках мельчайших каналов, по которым движутся жидкие частицы. При изменении давления в пластах природный газ растворяется в жидкости или выделяется из раствора.

Особенности движения жидкости и газа в пластах часто объяс­няются высокими пластовыми температурами и давлениями. Следова­тельно, чтобы наиболее рационально разрабатывать месторождение нефти или газа, надо знать не только подземную гидромеханику, но и гео­логию, геофизику, физику пласта и др. Рациональные методы добычи нефти и газа выбирают с учетом отраслевой экономики, техники экс­плуатации или технологии нефтедобычи. В нашу задачу не входит освещение вопросов, связанных с перечисленными дисциплинами.

Подземная гидравлика — наука, применяемая не только для решения вопросов рациональной разработки нефтяных и газовых залежей. Область использования её в различных отраслях народного хозяйства обширна. Гидротехнические сооружения (плотины, ка­налы, шлюзы, водоспуски и др.) проектируют на основе законов дви­жения воды в грунтах. Вода просачивается под основаниями этих сооружений, а иногда подземный поток вымывает грунт под ними, что может вызвать аварию. Важно предусмотреть возможность та­кого вымывания и найти меры борьбы с ними. Законы подземной гидромеханики лежат в основе расчётов, относящихся к водоснабжению, ирригации, подземной газификации угля и др.

Настоящее пособие посвящается вопросам подземной гидравлики в аспекте их приложения к проблемам добычи нефти и газа. Первые исследования проблемы движения нефти и газа в пластах, базировавшиеся на известных законах гидромеханики, появились в начале двадцатых годов нашего столетия. В настоящее время про­ектирование разработки нового месторождения нефти и газа, а также эксплуатация скважин не мыслятся без широкого применения зако­нов подземной гидравлики. Как правильно расставить скважины в данном пласте; сколько скважин, в какой последовательности надо вводить в пласт; какой режим работы в них поддерживать; какой рабочий агент — воду или газ — следует нагнетать в пласт для поддержания давления, и в каком количестве; как регулировать и направлять движение жидкости или газа в пласте — эти и многие другие вопросы решаются сейчас на основе подземной гидравлики.

Глава II

ЭЛЕМЕНТЫ ТЕОРИИ ФИЛЬТРАЦИИ

Явление фильтрации

Под фильтрацией понимают движений (просачивание) жидкости или газа или газожидкостной смеси через твердое тело, имеющее пустоты, одни из которых называют порами, другие трещинами. Мельчайшие пустоты обладают тем свойством, что силы молекуляр­ного взаимодействия между жидкостью и твердыми стенками очень велики. Они образуют молекулярные поры. В самых больших пусто­тах взаимодействие жидкости со стенками лишь частично влияет на ее движение. Такие пустоты называются кавернами. Промежуточное место между молекулярными порами и кавернами занимают просто поры. Твердое тело, содержащее поры, представляет собой пористую среду: песок, песчаник, известняк.

Если внутри твердого тела возникли трещины, такое тело являет собой пример трещиноватой среды. Растресканность горных пород макротрещинами и микротрещинами, не смещающими слои пород друг относительно друга, можно объединить под термином «трещиноватость». Пористый коллектор нефти и газа, наделенный к тому же свойством трещиноватости, есть представитель пористо-трещино­ватой среды.

Жидкость, газ, смесь жидкости и газа, другими словами - вся­кая текучая среда, часто именуется в зарубежной литературе соби­рательным термином флюид (fluid), если не ставится задача выделить характерные особенности движения данной среды.

Движение текучей среды через поры или трещины возможно, если некоторые из пор или трещин сообщаются между собой. Флюид, заполняющий сообщающиеся поры или трещины, образует непрерыв­ную среду (континуум), занимающую некоторую часть всего про­странства, принадлежащего объему пористой или трещиноватой среды. Мы будем считать, что в любом как угодно малом объеме пори­стой или трещиноватой среды находится жидкость, газ или газожид­костная смесь. Чрезвычайно малые размеры поровых каналов, их неправильная форма, большая поверхность шероховатых стенок — все это создает огромные сопротивления движению жидкости и газа (рис.1). Эти сопротивления служат главной причиной очень низкой скорости перемещения жидкости и газа в пористой среде; скорости в процессе фильтрации оказываются значительно более низкими, чем скорости движения в трубах или открытых руслах.

Если объем пространства, занятого порами, не изменяется или изменяется так, что его изменениями можно пренебрегать, пористая среда считается недеформируемой. Если же под влиянием упругих сил происходят такие изменения объема перового или трещиноватого пространства, величиной которых пренебрегать нельзя, среду следует рассматривать как упругую.

Рис. 1. Шлиф нефтяного песчаника

Теорию фильтрации нефти и газа в природных пластах характеризуют следующие особенности.

1. Невозможность изучать движение флюидов в пластах прямым применением обычных методов гидродинамики, т. е. решением уравне­ний движения вязкой жидкости для области, представляющей собой совокупность всех пор.

2. Сочетание очень разных масштабов фильтрационных процессов, определяемых различными характерными размерами, отличающимися по величине на многие порядки: размер пор (единицы и десятки микрометров), диаметр скважин (десятки сантиметров), расстояние
между скважинами (сотни метров), протяженность месторождений
(десятки километров). Масштаб неоднородности пластов вдоль и
поперёк их простирания может иметь практически любые значения.

3. Ограниченность и неточность сведений о строении и свойствах
пласта и пластовых флюидов, не позволяющих построить однозначную
модель пластовой залежи.

Эти особенности приводят к формулировке основных модельных представлений и разработке методов подземной гидромеханики, направ­ленных, прежде всего, на установление качественных закономерностей процессов и на создание расчетных схем, мало чувствительных к точ­ности исходных данных. При этом познавательная и практическая ценность получаемых результатов в значительной степени определяется четкостью постановки расчетной задачи и глубиной предварительного анализа имеющихся данных.

Пористость и просветнось.

Под пористой средой понимается множество твердых частиц, тесно прилегающих друг к другу, сцементированных или несцементированных, пространство между которыми (поры, трещины) может быть заполнено жидкостью или газом.

Ввиду того, что поровые каналы имеют неправильную форму и са­мые разнообразные размеры, невозможно исследовать движение час­тиц жидкости или газа по всему множеству каналов; невозможно точно знать формы и размеры каждого из этого множества каналов, прорезающих толщу реальной пористой породы. С самого начала раз­вития теории фильтрации пошли по пути построения упрощенных моделей реальной пористой среды.

Предположим, что пористая среда недеформируема. Так как движение вязкой жидкости хорошо иссле­довано в трубах а 6

цилиндрической формы, принимают, Рис. 2. Элемент фиктивного грунта.

например, все поры цилиндрическими. Модель пористой среды, построенная на ос­нове допущения, что все поры — узкие цилиндры, расположенные параллельно друг другу, называется моделью идеального грунта.

Другой моделью пористой среды в виде множества шарообразных частиц одинакового диаметра является модель фиктивного грунта. По идее Ч. Слихтера, все шарообразные частицы, образующие дан­ную пористую среду, уложены во всем её объёме одинаковым образом по элементам из восьми шаров. Наименее плотная укладка шаров — та, при которой центры восьми шаров помещаются в вершинах куба (см. рис. 2, а).

Наиболее плотная укладка получается при расположении цен­тров восьми шаров в вершинах ромбоэдра с углом ромба = 60° (рис. 2,6). Поровое пространство природного пласта, ввиду сложности и нере­гулярности его структуры, можно рассматривать как систему с большим числом однородных элементов, слабо связанных между собой. Из статистической физики известно, что такие системы могут быть описаны как некоторые сплошные среды, свойства которых не выражаются через свойства составляющих элементов, а являются усредненными характе­ристиками достаточно больших объёмов среды.

Макроскопическое фильтрационное течение пластовых флюидов проявляется как совокупность множества отдельных микродвижений в неупорядоченной системе поровых «каналов». С возрастанием числа таких микродвижений начинают проявляться статистические законо­мерности, характерные для движения в целом, но не для одного порового канала или нескольких каналов.

Это позволяет в качестве исходного допущения теории фильтрации, так же как и в гидродинамике принять, что пористая среда и насыщаю­щие ее флюиды образуют сплошную среду, т.е. заполняют любой выделенный элементарный объем непрерывно. Это накладывает опреде­ленные ограничения на понятие «элементарного объема» порового пространства. Под «элементарным объемом» в теории фильтрации понимают такой физически бесконечно малый объем, в котором заклю­чено большое число пор и зерен, так что он достаточно велик по сравнению с размерами пор и зерен породы. Для такого элементарного объема вводятся локальные усредненные характеристики системы флюид-пористая среда. В применении к меньшим объемам выводы теории фильтрации становятся несправедливыми.

Рассмотрим основные характеристики пористой среды. Если не учитывать силовое взаимодействие между твердым скелетом породы и прилегающими к нему частицами флюида, то пористую среду можно рассматривать как границы области, в которой движется жидкость. Тогда свойства пористой среды можно описать некоторыми средними геометрическими характеристиками.

Важнейшая из них - коэффициент пористости (или просто пористость) m , определённый для некоторого элемента пористой среды как отношение объёма 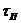, занятого порами в этом элементе, к его общему объёму . . (II.1)

Равенство (1.1) определяет среднюю пористость рассматривае­мого элемента. Если свойства этого элемента изменяются от точки к точке[1], то можно ввести понятие локальной пористости. Для этого, выбрав некоторую точку пористой среды, мысленно окружим её элемен­том объёма и найдем среднюю пористость этого элемента. Локальная пористость определяется как предел этой средней пористости при стягивании объёма элемента к элементарному объёму.

Обычно различают полную и эффективную пористости. При опреде­лении последней учитываются лишь соединенные между собой поры, которые могут быть заполнены жидкостью извне. При изучении процес­сов фильтрации важна именно эффективная пористость. Поэтому в дальнейшем под пористостью будем понимать активную или эффектив­ную пористость.

Наряду с пористостью т иногда вводится понятие «просветности» , определяемой для каждого сечения, проходящего через данную точку, как отношение площади активных пор в сечении ко всей площади сечения : . (II.2)

При определенных допущениях можно доказать, что в данной точке пласта просветность не зависит от выбора направления сечения и равна пористости: .

Коэффициент пористости одинаков для геометрически подобных сред; он не характеризует размеры пор и структуру порового прост­ранства. Поэтому для описания пористой среды необходимо ввести также некоторый характерный размер порового пространства. Сущест­вуют различные способы определения этого размера. Естественно, например, за характерный размер принять некоторый средний размер порового канала d или отдельного зерна пористого скелета.

Простейший геометрический параметр, характеризующий размер порового пространства - эффективный диаметр d_эф частиц грунта. Он определяется в результате механического анализа грунта. Эффектив­ным диаметром частиц, слагающих реальную пористую среду, назы­вается такой диаметр шаров, образующих фиктивный грунт, при кото­ром гидравлическое сопротивление, оказываемое фильтрующейся жид­кости в реальном и эквивалентном фиктивном грунте, одинаково. Однако на практике эффективный диаметр зерен d_эф является трудно определяемой величиной (особенно для сцементированных песчаников). Поэтому теория Слихтера не нашла широкого практического примене­ния.

Рис. 3 Схема наклонного пласта.

В середине прошлого столетия в результате экспериментального изучения движения воды через песчаные фильтры был установлен основной закон фильтрации — закон Дарси (или линейный закон фильтрации). Этот закон является хронологически первым законом теории фильтрации. Его можно записать так:

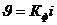, (II.8)

где К_ф — коэффициент фильтрации, имеющий размерность скорости; i — гидравлический уклон.

Коэффициент фильтрации К_ф зависит от свойств пористой среды и свойств фильтрующейся жидкости. Наибольшее влияние на этот коэффициент оказывают размеры частиц породы. Величина К_ф зависит также от формы частиц, степени шероховатости их поверхности, пористости среды, вязкости жидкости.

Видоизменим формулу (II.8).

Допустим, что в цилиндрической трубке, заполненной пористой средой, фильтруется жидкость в направлении, указанном стрелкой (рис. 3). Найдём потерю напора на данном участке длиной .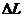

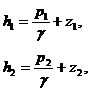Если пренебречь величиной скоростного напора, можем считать напоры 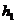и 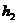равными соответственно:

(II.9)

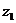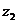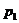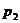где и — геометрические высоты крайних точек участка; и — давления в этих точках; 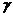— вес единицы объёма жидкости.

Потеря напора 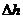запишется так: 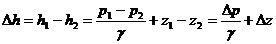, (II.10)

где 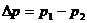— потеря давления, а .

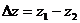Но гидравлический уклон 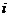можно с помощью формулы (II.10) записать так:

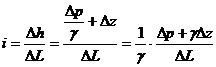. (II.11)

Подставив значение 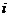из (II.11) в формулу (II.8), получим:

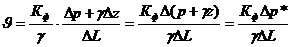, (II.12)

где 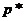— приведённое давление, причём 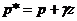. (II.13)

В случае горизонтального пласта в формуле (II.12) надо положить 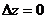; следовательно, закон Дарси запишется так: 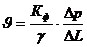. (II.14)

В символах дифференциального исчисления формула (II.14) (закон Дарси) имеет следующий вид:

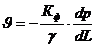, (II.15)

где 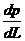— величина градиента давления, а знак минус в правой части показывает, что скорость фильтрации направлена в сторону понижения давления.

Итак, закон Дарси заключает в том, что скорость фильтрации пропорциональна градиенту давления.

Закон Дарси имеет силу, если соблюдаются следующие условия:

1) мелкозернистая пористая среда или достаточно узкие поровые каналы;

2) малая скорость фильтрации или небольшой градиент давления;

З) незначительные изменения скорости фильтрации или градиента давления.

Рис. 4. Зависимость параметра Дарси от числа Рейнольдса

Отсюда видно, что параметр Дарси представляет собой отношение силы вязкого трения к силе давления. Сравнивая равенство (II.23) и закон Дарси (II.17) (для случая горизонтального пласта, когда р^* = р), можно утверждать, что если справедлив закон Дарси, то

. (II.24)

Таким образом, равенство (II.24) должно выполняться при < 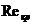Введение параметра упрощает исследование границы применимости линейного закона фильтрации. Действительно, если на оси абсцисс откладывать , а по оси ординат - , то поскольку = 0, при < 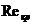графиком зависимости от будет прямая линия, совпадающая с осью абсцисс до тех пор, пока < 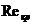. Как только на этом графике линия начнёт отделяться от оси абсцисс, сразу же обнаружится нарушение закона Дарси ( это соответствует значениям , Da<1, lgDa<0). Значение , при котором станет заметно отклонение упомянутой линии от оси абсцисс, и будет критическим значением для иллюстрации сказанного на рис. 4 на логарифмической сетке приведены зависимости от , представляющие результат обработки опытов по формулам В. Н. Щелкачева (табл. II.1). Данные на этом графике соответствуют области нелинейной фильтрации (lgDa<0) для различных образцов пористых сред.

Основываясь на этих соображениях, В. Н. Щелкачев провел критический анализ и сравнение формул, полученных разными исследователями, для определения в подземной гидромеханике и оценки возможных критических значений числа Рейнольдса 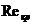, соответствующих верхней границе применимости закона Дарси. Результаты такого сопоставления приведены в табл. II.1. В первых двух строках таблицы даны соответственно формулы для и коэффициента гидравлического сопротивления 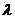, полученные разными авторами. В четвертой и пятой строках приведены соответственно критические значения , полученные самими авторами, и их уточнённые значения.

Наличие третьей строки табл. II.1, в которой дано произведение объясняется следующим. В области линейного закона фильтрации ( < 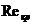) справедливо равенство II.24). Поэтому если произведение зависит только от параметра (см. графы 5—8 табл. II.1), то оно имеет постоянное значение (не зависящее от свойств пористой среды) в случае, если < 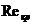. И только в этом случае можно получить <универсальный> прямолинейный график в координатах ( , ), соответствующий фильтрации различных флюидов через различные по свойствам пористые среды. Результаты обработки опытов подтверждают этот вывод.

На основе анализа данных, приведенных в табл. 1, можно сделать следующие выводы.

1. Несмотря на отмеченные недостатки результатов Н. Н. Павловского, есть основания для их сопоставления с соответствующими результатами трубной гидравлики. Важно подчеркнуть, что критические значения числа Рейнольдса, подсчитанные по формуле (II.22), намного меньше тех, которые в трубной гидравлике соответствуют переходу ламинарного течения в турбулентное. Это служит одним из доводов в пользу того, что причины нарушения закона Дарси при высоких скоростях фильтрации (увеличение влияния сил инерции по мере увеличения ) не следует связывать с турбулизацией течения. Отсутствие турбулентности при нарушении закона Дарси было доказано также прямыми опытами, изложенными Г. Шнебели.

Формулы Фэнчера, Льюиса и Бериса получены формальным введением в выражение для числа Рейнольдса эффективного диаметра в качестве характерного размера пористой среды, они не сопоставимы с результатами трубной гидравлики, дают слишком узкий диапазон изменения значений (см. графу 4 табл.1), мало обоснованы.

2. Во все другие формулы табл. II.1 (графы 5—9) в качестве характерного размера входят величины, пропорциональные , (где 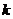— коэффициент проницаемости породы), методы определения которых хорошо известны. Формулы этой группы не имеют принципиальных преимуществ и одинаково удобны для практического использования. Для этих формул характерно то, что все они приводят к очень широким диапазонам изменения для различных пористых сред. И это представляется вполне естественным ввиду разнообразия свойств испытанных пористых сред. Кроме того, это свидетельствует о том, что ни в одну из предложенных формул для определения не входит полный набор параметров, позволяющий характеризовать сложную структуру пористых сред, использования для этой цели коэффициентов пористости и проницаемости явно недостаточно.

Вместе с тем, широкий диапазон изменения значений , можно разбить на сравнительно узкие интервалы, соответствующие различным группам образцов пористых сред. Это облегчает указание возможной верхней границы справедливости закона Дарси при движении флюида в какой-либо пористой среде.

Результаты такого разбиения для формулы В. Н. Щелкачева (см. табл.1, первая строка, пятая графа) приведены в табл.2.

Таблица 1

Определение верхней границы применимости закона Дарси по данным различных исследований (в табл. 1 )

Таблица 2

Глава III

ОСОБЕННОСТИ ФИЛЬТРАЦИИ

ПЛАСТАХ

Параметры трещиноватости

Рациональная разработка месторождений, приуроченных к трещиноватым пластам, будет способствовать дополнительной добыче нефти и газа. Отметим, что доля разведанных запасов нефти в трещиноватых пластах в общем балансе месторождений немного шара постоянно возрастает и уже сейчас составляет около 44%.

Уместно отметить, что если процессы фильтрации в поровых коллекторах хорошо изучены, то вопросам движения жидкости и газа в трещиноватых и трещиновато-пористых пластах стали уделять внимание сравнительно недавно, в основном в 60 гг. Эта область является молодой, перспективной областью подземной гидравлики и несомненно с большой будущностью.

Все коллекторы можно подразделить на две большие группы:

гранулярные (поровые) и трещиноватые. Емкость и фильтрация в гранулярном (поровом) коллекторе определяются структурой порового пространства породы, о чём подробно отмечалось в предшествующих параграфах главы II. Для второй группы характерно наличие развитой системы трещин.

Таким образом, трещиноватость пород создается развитыми системами трещин, густота которых зависит от состава пород, степени уплотнения, мощности, метаморфизма, структурных условий, состава и свойств вмещающей среды.

Трещиноватые коллекторы подразделяются на:

1) коллекторы смешанного типа, для которых ёмкостью служат трещины, каверны, микрокарсты, стилолиты, поровые пространства; ведущая роль в фильтрации нефти и газа принадлежит развитой системе микротрещин, сообщающих эти пустоты между собой; 2) чисто трещинного типа — ёмкостью служат трещины и по ним же

осуществляется фильтрация.

Коллекторы смешанного типа в свою очередь подразделяются на подклассы: трещиновато-пористые, трещиновато-каверновые, трещиновато-пористо-каверновые коллекторы и т. д. Каждый такой подкласс определяется тем, какие категории пустот являются главными вместилищами для нефти (газа). Так, в трещиновато-пористом коллекторе основные запасы нефти (газа) содержатся в порах, а фильтрация осуществляется по развитой системе микротрещин.

Одним из важнейших параметров, характеризующих трещиноватый коллектор, является трещиноватость (коэффициент трещиноватости, нааываемый иногда в литературе трещиной пористостью). Трещиноватостью называется отношение объёма трещин образца ко всему объему образца трещиноватаой среды: (III.1)

Рис. 5. Схема трещиновато-пористой среды.

Выражается эта величина обычно в процентах. Трещиновато пористые коллекторы имеют два типа естественных пустот:

а) межзерновая (первичная) пористость, аналогичная пористости для обычных песков песчаников;

б) вторичная пористость (трещиноватость), обусловленная развитием трещиноватости, появившейся за счет различных причин. Пустоты этого типа имеют большие раскрытия, чем обычные раскрытия пор, и в значительной степени обусловливают фильтрационные свойства коллектора.

В соответствии со сказанным такие коллекторы рассматриваются как совокупность двух разномасштабных пористых сред (рис. 5) системы трещин (среда 1), где пористые блоки играют роль “зёрен”, а трещины — роль извилистых “пор”, и системы пористых блоков (среда 2).

Для трещиновато-пористого коллектора помимо коэффициента трещиноватости следует еще ввести коэффициент пористости , характеризующий среду 2. Тогда общую (суммарную) пористость трещиновато-пористого коллектора можно получить, если к коэффициенту трещиноватости прибавить коэффициент межзерновой пористости пористых блоков .

Другим важным параметром трещиноватой среды является густота трещин.

Густота трещин есть отношение числа трещин 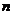, секущих нормаль, к длине нормали, проведённой к поверхностям, образующим трещины:

. (III.2)

Густота трещин имеет размерность, обратную единице длины.

Если трещиноватый пласт моделируется одной сеткой горизонтальных трещин некоторой протяженности в фильтрующей среде, причем все трещины одинаково раскрыты и равно отстоят друг от друга, то густота их — число трещин, приходящихся на единицу мощности пласта. Тогда коэффициент трещиноватости пласта

, (III.3)

где — раскрытие трещин; — характерные линейные размеры образца; — мощность (рис. 6).

Рис. 6. Схема модели трещиновато- Рис. 7. Схема модели трещиноватого пласта

Проницаемость пласта

В т р е щ и н о в а т о м п л а с т е зависимость между скоростью фильтрации 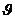и средней скоростью движения по трещинам 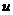выражается в виде:

, (III.5)

или по известной из гидромеханики формуле Буссинеска для средней скорости течения жидкости между двумя плоскими неподвижными параллельными стенками:

. (III.6)

На основании (III.5), (III.4) выражение (III.б) принимает форму:

. (III.7)

Параметр проницаемости изотропного трещиноватого пласта, как это следует из (III.7)

. (III.8)

Если учесть, что в системе СИ проницаемость 1 дарси = 1,02 х 10^-12 м², то для трещиноватого пласта

. (III.8а)

Для трещиновато-пористого пласта общая проницаемость определяется как сумма межзерновой и трещинностей проницаемостей трещиноватого пласта, рассмотренной выше (III .8).

В продуктивных трещиноватых пластах горное давление, определяющее общее напряжённое состояние среды, уравновешивается напряжениями в скелете породы и давлением жидкости в трещинах. При постоянстве горного давления снижение пластового давления за счёт отбора жидкости из пласта приводит к увеличению нагрузки на скелет среды. С уменьшением пластового давления (давления жидкости в трещинах) уменьшаются усилия, сжимающие зерна (пористые блоки) трещиноватой породы. Значение этого фактора наряду со значительными силами инерции следует учитывать при исследовании процессов фильтрации в трещиноватом пласте. Таким образом, на объём пространства трещин в трещиноватом коллекторе влияют в основном два фактора: 1) увеличение объёмов зерен с падением пластового давления; 2) увеличение сжимающих усилий на скелет продуктивного пласта.

Полагая, что в трещиноватом пласте преобладают упругие деформации и учитывая, что горное давление постоянно, а с изменением давления в жидкости, газе изменяются главным образом раскрытия трещин б, можно так оценить изменение раскрытия трещин от давления:

, (III.9)

где — упругая константа; — коэффициент Пуассона; Е — модуль Юнга; 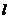- среднее расстояние между трещинами.

Разрешая уравнение (III.9) с учетом (III.8а), получим формулу для определения параметра проницаемости в д е ф о р м и р у е м о м т р е щ и н о в а т о м п л а с т е:

, (III.10)

где — комплексный параметр трещиноватой среды, зависящий от упругих свойств и геометрии трещин;

. (III.11)

Механизм деформации в трещиновато-пористых пластах более сложен, чем в коллекторах чисто трещинного типа, рассмотренных выше. Однако можно отметить, что в трещиновато-пористых средах под внешними воздействиями вначале деформируется система трещин (среда 1, рис. 5); причём истинное напряжение этой системы играет роль внешней нагрузки для системы пористых блоков (среда 2, рис. 5).

Глава IV

В ПОРИСТОЙ СРЕДЕ

Потенциальное движение

Установившийся фильтрационный поток в пласте, в котором давление можно выразит в функции только одной линейной координаты, считается одномерным.

Представим себе в пористой или трещиноватой среде трубку тока переменного сечения (рис. 8) и допустим, что во всех сечениях, нормальных по отношению к кривой — оси трубки, площади сечения 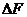выражаются в функции длины 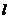, отсчитываемой вдоль оси трубки

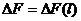. (IV.1)

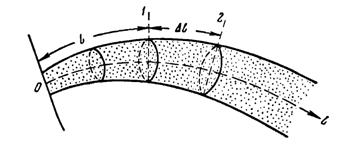Рис. 8. Схема трубки тока в фильтрующей среде.

Пусть каждая нормальная к оси трубки поверхность является изобарической, т. е. поверхностью равного давления р. Если трубка тока неизменяема, давление можно считать зависящим только от одной линейной координаты 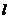, а следовательно, поток — одномерным.

Из условия неразрывности потока следует, что при установившейся одномерной фильтрации расход массы жидкости в единицу времени через все изобарические поверхности в трубке тока будет один и тот же.

Введём алгебраическую величину – массовую скорость фильтрации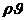

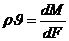,(IV.2)

где М — расход массы жидкости через поверхность равного давления; его мы можем назвать массовым дебитом. Полный установившийся фильтрационный поток можно рассматривать как непрерывную совокупность неизменяемых трубок тока, а массовый дебит М — как сумму расходов через соответствующие поверхности сечений всех этих трубок тока.

С другой стороны, в соответствии с законом Дарси (II.17) модуль массовой скорости фильтрации 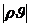можно записать так:

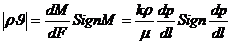, (IV.3)

где 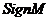и 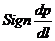— символы, показывающие, что в равенстве (IV.3) следует ставить тот знак, какой имеет в первом случае М, во втором 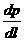. (Латинское signum — знак).

Из равенства (IV.3) получим:

Наши рекомендации