Математика: алгебра и начала математического анализа; геометрия

МАТЕМАТИКА: АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА; ГЕОМЕТРИЯ

для студентов специальностей:

Сестринское дело

Базовая подготовка

среднего профессионального образования

Оренбург

2016

Методические указанияпо выполнению самостоятельных работ по учебной дисциплине Математика: алгебра и начала математического анализа; геометрия (базовая подготовка) разработаны на основе рабочей программы учебной дисциплины Математика: алгебра и начала математического анализа; геометрия по всем специальностям и Положения о самостоятельной работе студентов (Приказ №252 от 30.04.2014 года).

Разработчик(и):

ОМК – СП ОрИПС – филиала СамГУПС преподаватель Л.В. Шатских_

(место работы) (занимаемая должность) (инициалы, фамилия)

ОМК – СП ОрИПС – филиала СамГУПС преподаватель А.А. Бакирова_

(место работы) (занимаемая должность) (инициалы, фамилия)

Рассмотрено и одобрено на заседании предметной (цикловой) комиссии математических и общих естественнонаучных дисциплин Протокол №_______ от «_____» ______________ 20____г. Председатель ПЦК ________________________ /А.В.Портнов/

Оглавление

Введение………………………………………………………………………………….4

Самостоятельная работа №1……………………………………………………………..6

Самостоятельная работа №2………………………………………………………….. ...9

Самостоятельная работа №3…………………………………………………………….12

Самостоятельная работа №4……………………………………………………………..16

Самостоятельная работа №5……………………………………………………………...21

Самостоятельная работа №6……………………………………………………………...26

Самостоятельная работа №7………………………………………………………………30

Введение

Методические указания по выполнению внеаудиторной самостоятельной работы по естественно - научной дисциплине математика предназначены для студентов, обучающихся по программам общего образования.

Объем самостоятельной работы студентов определяется государственным образовательным стандартом среднего профессионального образования (ФГОС СПО) обучающихся по программам общего образования.

Выполнение внеаудиторной самостоятельной работы является обязательной для каждого студента, её объём в часах определяется действующим рабочим учебным

планом Оренбургского медицинского колледжа по данной специальности.

Самостоятельная внеаудиторная работа по математике проводится с целью:

- систематизации и закрепления полученных теоретических знаний студентов;

- углубления и расширения теоретических знаний;

- развития познавательных способностей и активности студентов, самостоятельности, ответственности и организованности;

- формирования самостоятельности мышления, способностей к саморазвитию, самосовершенствованию и самореализации.

Внеаудиторная самостоятельная работа выполняется студентом по заданию преподавателя, но без его непосредственного участия. По математике используются следующие виды заданий для внеаудиторной самостоятельной работы:

для овладения знаниями: чтение текста (учебника, дополнительной литературы), работа со справочниками, учебно-исследовательская работа, использование аудио- и видеозаписей, компьютерной техники и Интернета;

- для закрепления и систематизации знаний: повторная работа над учебным материалом (учебника, дополнительной литературы, аудио- и видеозаписей), составление плана и алгоритма решения, составление таблиц для систематизации учебного материала, ответы на контрольные вопросы, подготовка сообщений к выступлению на уроке, подготовка сообщений, докладов, рефератов, тематических кроссвордов;

-для формирования умений: выполнение схем, обработка нормативов и действий, подготовка к деловым играм.

Учебная дисциплина «Математика» предполагает 78 часов самостоятельной работы учащихся.

В результате освоения дисциплины обучающийся должен знать/понимать:

¾ значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;

¾ значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;

¾ универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;

¾ вероятностный характер различных процессов окружающего мира.

В результате освоения дисциплины обучающийся должен уметь:

Алгебра

¾ выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;

¾ проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;

¾ вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;

¾ использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

¾ практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;

¾ понимания взаимосвязи учебного предмета с особенностями профессий и профессиональной деятельности, в основе которых лежат знания по данному учебному предмету.

Функции и графики

¾ определять значение функции по значению аргумента при различных способах задания функции;

¾ строить графики изученных функций;

¾ описывать по графику и в простейших случаях по формуле, поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;

¾ решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;

¾ использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

¾ описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;

¾ понимания взаимосвязи учебного предмета с особенностями профессий и профессиональной деятельности, в основе которых лежат знания по данному учебному предмету.

Уравнения и неравенства

¾ решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;

¾ составлять уравнения и неравенства по условию задачи;

¾ использовать для приближенного решения уравнений и неравенств графический метод;

¾ изображать на координатной плоскости множества решений простейших уравнений и их систем;

¾ использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

¾ построения и исследования простейших математических моделей;

¾ понимания взаимосвязи учебного предмета с особенностями профессий и профессиональной деятельности, в основе которых лежат знания по данному учебному предмету.

Геометрия

¾ распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;

¾ описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;

¾ анализировать в простейших случаях взаимное расположение объектов в пространстве;

¾ изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;

¾ строить простейшие сечения куба, призмы, пирамиды;

¾ решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);

¾ использовать при решении стереометрических задач планиметрические факты и методы;

¾ проводить доказательные рассуждения в ходе решения задач;

¾ использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

¾ исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;

¾ вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства;

¾ понимания взаимосвязи учебного предмета с особенностями профессий и профессиональной деятельности, в основе которых лежат знания по данному учебному предмету.

Перед выполнением внеаудиторной самостоятельной работы студент должен

внимательно выслушать инструктаж преподавателя по выполнению задания,

который включает определение цели задания, его содержание, сроки выполнения,

ориентировочный объем работы, основные требования к результатам работы,

критерии оценки. В процессе инструктажа преподаватель предупреждает студентов

о возможных типичных ошибках, встречающихся при выполнении задания. В пособии

представлены как индивидуальные, так и групповые задания в зависимости от цели, объема, конкретной тематики самостоятельной работы, уровня сложности. В качестве форм и методов контроля внеаудиторной самостоятельной работы студентов используются аудиторные занятия, зачеты, тестирование, самоотчеты, контрольные работы.

Критериями оценки результатов внеаудиторной самостоятельной работы студента являются:

- уровень освоения студентом учебного материала;

- умение студента использовать теоретические знания при выполнении практических задач;

- сформированность общеучебных умений;

- обоснованность и четкость изложения ответа;

- оформление материала в соответствии с требованиями.

В методических указаниях приведены теоретический (справочный) материал в соответствии с темой работы, обращение к которому поможет выполнить задания самостоятельной работы; вопросы для самоконтроля, подготавливающие к выполнению заданий и сами задания.

Самостоятельная работа №1 – 8 часов.

Тема: Решение упражнений по основам тригонометрии

Студент должен :

Знать:

основные тригонометрические формулы; понятия обратных тригонометрических функций; способы решения простейших тригонометрических уравнений

Уметь :

упрощать тригонометрические выражения; доказывать тождества; решать простейшие тригонометрические уравнения, а также несложные уравнения, сводящиеся к квадратным.

Пример 2.

2 sin x -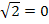

2 sin x =

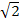
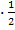
sin x =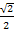

x =

Ответ. x =

Пример 3.

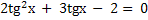
Пусть tg x = t

2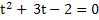

D = 9+ 4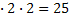

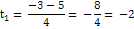
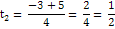
tg x = -2 tg x =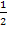

x = arctg (-2) + 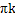x = arctg +

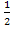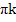
x = - arctg 2 +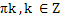

Ответ. x = - arctg 2 +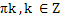

x = arctg +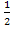

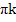
Пример 4.

cos 2x + cos 6x = 0

2cos 4x 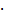cos (-2)x = 0 cos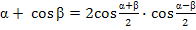

2 cos 4x 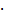cos 2x = 0

cos 4x = 0 cos 2x = 0

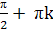
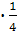4x = 2x =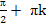

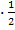
Самостоятельная работа

«Решение тригонометрических уравнений»

Часть А

	Вариант №1		Вариант №2
А1		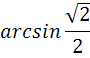А1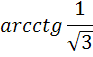
А2		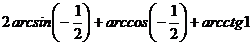А2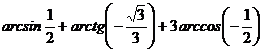
А3		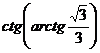А3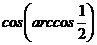

Часть В

	Вариант №1		Вариант №2
В1		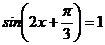В1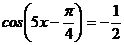
В2		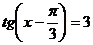В2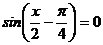

Часть С

	Вариант №1		Вариант №2
С1		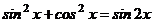С1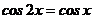
С2		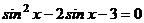С2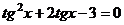
С3		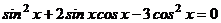С3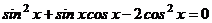

Ответы к самостоятельной работе

«Решение тригонометрических уравнений»

Часть А

	Вариант №1		Вариант №2
А1		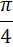А1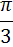
А2		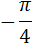А2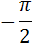
А3		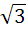А3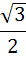

Часть В

	Вариант №1		Вариант №2
В1		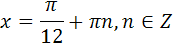В1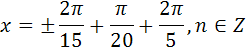
В2		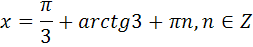В2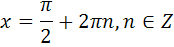

Часть С

	Вариант №1		Вариант №2
С1		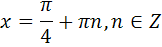С1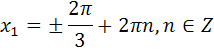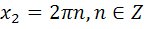
С2		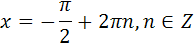С2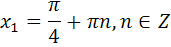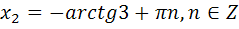
С3		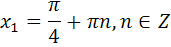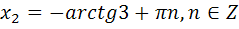С3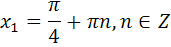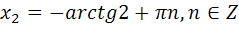

Критерии выставления оценок:

Оценка «5» ставится за правильное решение части А, В и одного задания части С

Оценка «4» ставится за правильное решение части А и части В

Оценка «3» ставится за правильное решение части А и одного задания части В

Оценка «2» ставится за неправильное решение всех заданий.

Самостоятельная работа №2 - 10 часов.

Тема: - Построение графиков функций

Студент должен :

Знать:

свойства и графики показательной, логарифмической и степенной функции

Уметь :

строить графики показательных, логарифмических функций при различных основаниях и на них иллюстрировать свойства функций; преобразовывать эти графики путем сдвига и деформации

Пример 2.

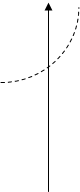
Построить график функции :

Y=-3^x

График данной функции строится двумя шагами:

1) Строится график функции y=f(x), в данном случае это Y= 3^x

2)

y

Полученный график Y= 3^x отображаем относительно оси ОХ , опираясь на шестое простейшее правило преобразования графиков функций

Оформление:

x

Y= - 3^x

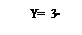
x		-1
y		⅓

1)Y= 3^x

2)Y= - 3^x

Пример 3

Построить график функции :

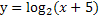
График данной функции строится двумя шагами:

1) Строится график функции y=f(x), в данном случае это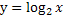

2) Полученный график 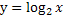смещаем влево на 5 единиц.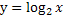

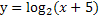
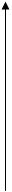
y

Оформление:

1)

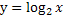
2)

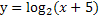
Пример 4

Построить график функции : -5

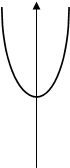
Y=x²+3

График данной функции

и строится двумя шагами:

1)Строится график функции y=f(x), в данном случае это y=x².

2)Полученный график смещаем на 3 единицы вверх, опираясь на второе простейшее правило преобразования графиков функций(График функции у=f(x)+в получается из графика функции у=f(x) сдвигом его вдоль оси ОY на а единиц (вверх при в>0 вниз при в<0)

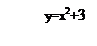Оформление:

x	-1	-2
y

1)y=x²

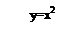
2)y=x²+3

3

Пример 5 (дополнительное)

Построить график функции :

Y=3(x+2)²-4

График данной функции строится четырьмя шагами:

1) Строится график функции y=f(x), в данном случае это y=x².

2) Следующий шаг – построение Y=(x+2)², т.е. смещаем график на 2 единицы влево, относительно оси ОХ.

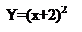Строим график функции Y=3(x+2)², т.е. сужаем график

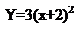
3) Смещаем график на 4 единицы вниз.

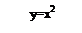Оформление:

1) y=x²

2) Y=(x+2)²

3) 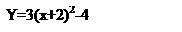Y=3(x+2)²

4) Y=3(x+2)²-4

1. Построить график функции и перечислите их свойства

Номер варианта	Функции
Вариант 1.	а) y=2-3x б) y=-x2+2x, xϵ[-1;3]
Вариант 2.	а) y=5-2x б) y=3-x2-2x, xϵ[-4;2]
Вариант 3.	а) y=2-4x б) y=x2-4x+1, xϵ[-1;5]
Вариант 4.	а) y=2x-3 б) y=-x2+6x, xϵ[-1;4]
Вариант 5.	а) y=3x-1 б) y=x2-2x+4, xϵ[-1;4]
Вариант 6.	а) y=2x-4 б) y=x2-6x+1, xϵ[0;6]
Вариант 7.	а) y=-2x+4 б) y=-x2+2x-5, xϵ[-2;2]
Вариант 8.	а) y=3x-4 б) y=-x2+4x-5, xϵ[-1;5]
Вариант 9.	а) y=4x-2 б) y=2x2-2x+2, xϵ[-2;4]
Вариант 10.	а) y=-x+5 б) y=4-x2, xϵ[-3;3]

2.Используя таблицу показаний, постройте графики температуры, пульса и артериального давления на температурном листе. Отмечайте показания только утра.

Условные обозначения: П – пульс, АД – артериальное давление, Т° – температура, у – утро, в – вечер.

Постройте три графика в системе координат, отображающих зависимость Т°, АД, П отдня. Масштаб выберите самостоятельно.

Т° АД П

день день день

Таблица показаний к температурному листу

День
Т°	38,7	38,1	37,5	37,5	37,6	37,9	37,2
АД	120/80	110/70	110/70	100/60	120/90	110/70	100/60
П

День
Т°	36,8	36,9	36,5	36,7	36,6	36,5	36,6
АД	110/80	115/75	120/80	110/75	115/65	100/60	95/60
П

3.

	Код формы по ОКУД
	Код учреждения по ОКПО
Министерство здравоохранения	Медицинская документация
РФ	Форма N 004/у
	Утверждена Минздравом СССР
наименование учреждения	04.10.80 г. N 1030

ТЕМПЕРАТУРНЫЙ ЛИСТ

Карта №			Палата №
Фамилия, имя, отчество больного

Дата

День болезни

День пребывания в стационаре

П

АД

Т°

у

в

у

в

у

в

у

в

у

в

у

в

у

в

у

в

у

в

у

в

у

в

у

в

у

в

у

в

у

в