Основы теории случайных процессов

К. П. КАДОМСКАЯ

ОСНОВЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ

Учебное пособие

для студентов 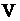курса и магистрантов факультета энергетики

Новосибирск

Кадомская К.П. Основы теории случайных процессов. Учебное пособие/Новосибирск: Изд-во НГТУ, 1999. – с.

В пособии рассматриваются основы теории случайных процессов, подкрепленные соответствующими примерами. Излагаются основные вероятностные характеристики случайных процессов, а также линейные и нелинейные их преобразования. Приводится методика оптимизации линейных систем, основанная на минимизации ошибок на их выходе. Даются краткие сведения из статистики случайных процессов.

Рецензент д-р техн. наук, профессор

В.З. Манусов

Работа подготовлена кафедрой техники и электрофизики высоких

напряжений

Новосибирский государственный

технический университет, 1999 г.

ОГЛАВЛЕНИЕ

Стр.

ПРЕДИСЛОВИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ СЛУЧАЙНЫХ

ПРОЦЕССОВ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.1. Случайные процессы и способы их характеристик . . . . . . . . .

1.2. Основные свойства математического ожидания и

корреляционной функции случайного процесса . . . . . . . . . . .

2. КЛАССИФИКАЦИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ. . . . . . . . . .

2.1. Стационарные процессы . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.2. Нормальные процессы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.3. Эргодические процессы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.4. Марковские процессы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ СТАЦИОНАРНЫХ

СЛУЧАЙНЫХ ПРОЦЕССОВ . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СТАЦИОНАРНЫХ

СЛУЧАЙНЫХ ПРОЦЕССОВ . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.1. Линейные операторы и их воздействия на случайные

процессы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.2. Линейные преобразования случайных процессов при исполь-

зовании понятия спектральной плотности . . . . . . . . . . . . . . . . .

5.ПРИМЕНЕНИЕ ТЕОРИИ СТАЦИОНАРНЫХ ПРОЦЕССОВ

К РЕШЕНИЮ ЗАДАЧ, СВЯЗАННЫХ С АНАЛИЗОМ И СИНТЕ-

ЗОМ ДИНАМИЧЕСКИХ СИСТЕМ . . . . . . . . . . . . . . . . . . . . . . . . . .

5.1. Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. .

5.2. Задача анализа динамической системы . . . . . . . . . . . . . . . . . . . .

5.3. Оптимизация параметров линейной системы при заданной

её структуре . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.4. Определение оптимальной линейной системы при незаданной

её структуре. Уравнение Винера-Хопфа и способ его решения

6. ВЫБРОСЫ СЛУЧАЙНЫХ ПРОЦЕССОВ . . . . . . . . . . . . . . . . . . . . .

6.1. Общие понятия. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.2. Математическое ожидание числа положительных выбросов . .

6.3. Математическое ожидание времени превышения процессом

X(t) заданного уровня . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7. НЕКОТОРЫЕ НЕЛИНЕЙНЫЕ ЗАДАЧИ ТЕОРИИ СЛУЧАЙНЫХ

ПРОЦЕССОВ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7.1 Метод статистической линеаризации . . . . . . . . . . . . . . . . . . . . . . .

…7.2. Исследование точности нелинейных систем . . . . . . . . . . . . . .. . .

8.ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ

ПО ДАННЫМ ОПЫТОВ . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . .. .

8.1. Статистическая оценка математического ожидания случайного

процесса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.2.Статистическая оценка корреляционной функции случайного

процесса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.3. Статистическая оценка спектральной плотности случайного

процесса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.4. Определение статистической оценки закона распределения

ординаты стационарного процесса . . . . . . . . . . . . . . . . . . . . . . . .

ЛИТЕРАТУРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

ПРЕДИСЛОВИЕ

Теория вероятностей возникла в XY111 веке и первое время развивалась как наука о событиях. С середины X1X века появились новые задачи, в которых требовалось не только устанавливать вероятность появления факта-события, но и необходимо было также установить, какие значения могли принимать те или иные случайные величины (СВ). СВ – это более общее понятие, включающее в себя понятие событий. Действительно, с каждым событием можно сопоставить случайную величину X=1, если событие происходит и X=0, если оно не происходит.

В 1827 году Р.Броуном было открыто хаотическое движение малых частиц, взвешенных в жидкости. Для описания этого явления понадобился аппарат, дающий возможность производить количественный анализ не случайных величин, а случайных процессов, протекающих во времени. Понятие случайных процессов (СП) или случайных функций (СФ) является обобщением понятия случайных величин, так как при определенном значении аргумента (времени) случайная функция является случайной величиной.

Так, например, случайным процессом является процесс изменения напряжения в какой-либо точке электрической сети под действием случайных изменяющихся во времени нагрузок в различных узлах этой сети.

В учебном пособии рассматриваются вероятностные характеристики случайных процессов и приводятся решения некоторых задач, связанных с анализом и синтезом динамических систем и выбросами СП. Даются краткие сведения из статистики СП.

При написании учебного пособия автор опирался на соответствующую главу из книги [1] и на опыт преподавания этого раздела курса теории вероятностей в Санкт-Петербургском и Новосибирском технических университетах.

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ СЛУЧАЙНЫХ

ПРОЦЕССОВ

Стационарные процессы

Случайный процесс называется стационарным, если его многомерный закон распределения зависит лишь от взаимного расположения моментов времени t₁, t₂, . . .t_n, т.е. не меняется при одновременном сдвиге этих моментов времени на одинаковые величины:

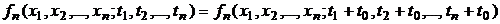. (2.1)

Если выражение (2.1) удовлетворяется при любом n, то такой процесс называется стационарным в узком смысле.

При n=1 выражение (2.1) приобретает вид:

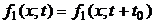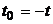
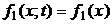и при , 2.2)

т.е. одномерный закон распределения стационарного процесса не зависит от времени. Следовательно, от времени не будут зависеть и характеристики случайного процесса, зависящие от одномерного закона распределения: математическое ожидание и дисперсия случайного процесса:

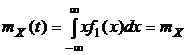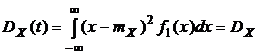, . (2.3)

При n=2 выражение (2.1) переписывается следующим образом:

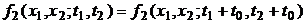и при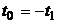

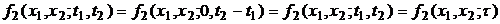, (2.4)

где .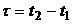

Следовательно корреляционная функция стационарного процесса, определяемая двумерным законом распределения, будет зависеть лишь от интервала времени t

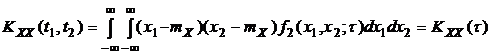. (2.5)

По определению А.Я.Хинчина процесс является стационарным в широком смысле, если условие стационарности (2.1) удовлетворяется лишь при n=1 и 2.

Следовательно, условия стационарности процесса в широком смысле можно сформулировать в виде:

· математическое ожидание и дисперсия такого процесса не зависят от времени - 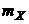и D_X;

· корреляционная функция процесса зависит лишь от интервала между сечениями по времени - .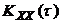

K_XX(t) является четной функцией своего аргумента:

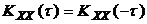. (2.6)

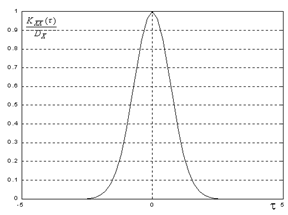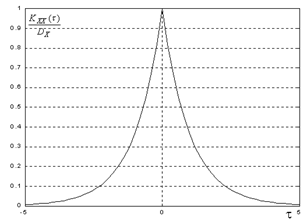
При решении практических задач часто применяются следующие аппроксимации K_XX(t):

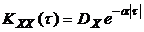
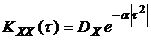
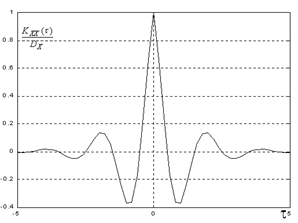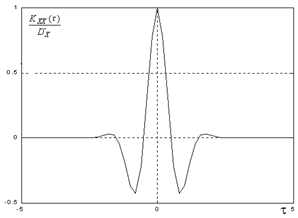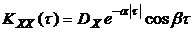
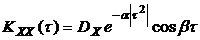
Следует помнить, что взаимная корреляционная функция представляет собой нечетную функцию:

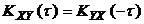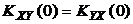, ( ). (2.7)

Нормальные процессы

Случайный процесс является нормальным, если нормальным является любой многомерный закон:

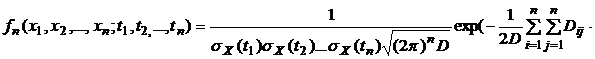
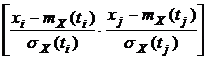× ), (2.8)

где 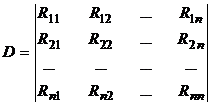(2.9)

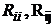- относительные собственные и взаимные корреляционные функции,

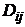- алгебраическое дополнение определителя (2.9), отвечающее элементу

матрицы .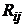

Есл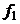и и 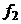отвечают свойствам стационарности и процесс нормален, то и 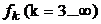также отвечают свойствам стационарности. Следовательно, для нормального процесса понятия стационарности в узком и широком смыслах совпадают.

Эргодические процессы

Стационарный процесс является эргодическим, если любая его характеристика, полученная усреднением множества реализаций, совпадает с результатами усреднения за достаточно большой интервал одной реализации, т.е.

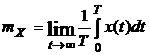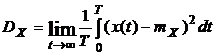, , (2.10)

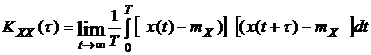. (2.11)

В случае эргодического процесса справедливо следующее соотношение:

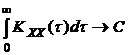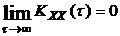( ). (2.12)

Приведем пример стационарного, но не эргодического процесса. Пусть

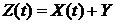, (2.13)

где X(t) – эргодический процесс, Y – случайная величина. Определим .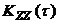

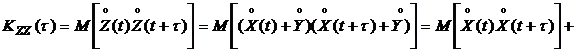
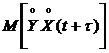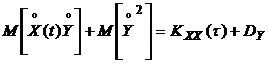+ . (2.14)

Поскольку 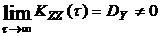, то случайный процесс 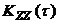не является эргодическим, хотя и сохраняет стационарность.

Действительно, различные реализации этого процесса имеют разные характеристики. На рис.2.1 приведены две реализации случайного процесса при 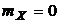и двух значениях случайной величины Y – y₁ и y₂. Из рисунка видно, что математическое ожидание реализации при Y=y₁ равно y₁, а при Y=y₂ – y₂.

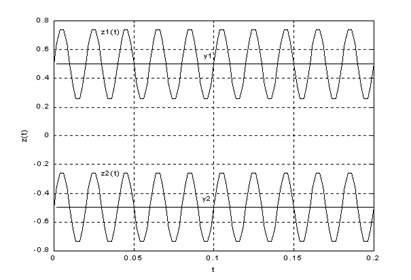Рис.2.1. Пример стационарного неэргодического процесса

Таким образом, по единственной реализации стационарного, но неэргодического процесса нельзя судить о характеристиках процесса в целом.

Марковские процессы

Если вероятностные свойства случайного процесса полностью определяются значением его ординаты в заданный момент времени и не зависят от значений ординат процесса в предыдущие моменты времени, то такой случайный процесс называется Марковским. Иногда такие процессы называют процессами без последействия.

СЛУЧАЙНЫХ ПРОЦЕССОВ

Если интеграл 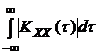сходится, т.е. стационарный процесс обладает свойством эргодичности, то корреляционная функция может быть представлена в виде двойного интеграла Фурье:

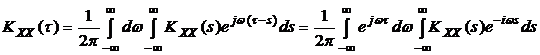. (3.1)

Введем обозначение

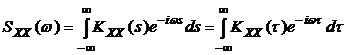. (3.2)

Тогда

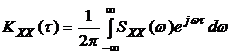. (3.3)

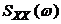называется спектральной плотностью случайного процесса , а прямое (3.2) и обратное (3.3) преобразования Фурье – преобразованиями Хинчина-Винера.

Поясним физический смысл введенного понятия спектральной плотности СП.

Рассмотрим простейший электрический контур, состоящий из источника напряжения и резистора с сопротивлением R=1 Ом (рис.3.1). Предположим, что на вход схемы подается напряжение в виде центрированного случайного процесса ( флуктуация напряжения) -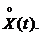

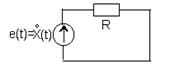Средняя мощность, поглощаемая в сопротивлении за

интервал времени Т, определится как .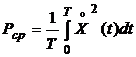

Рис.3.1 Но в случае эргодического процесса его дисперсия будет: 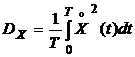. Следовательно 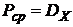. Дисперсия же процесса может быть выражена через его спектральную плотность:

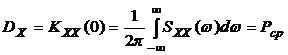. (3.4)

Средняя мощность, выделяемая в сопротивлении в частотном диапазоне 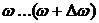, определится как:

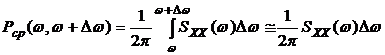. (3.5)

Из (3.5) следует, что

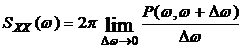. (3.6)

Таким образом, спектральная плотность характеризует распределение мощности флуктуационных потерь по частотам, т.е. может рассматриваться как плотность мощности флуктуационных потерь на различных частотах w, образующих непрерывный спектр.

Получим выражение для спектральной плотности процесса, характеризующегося корреляционной функцией вида 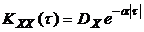. В этом случае

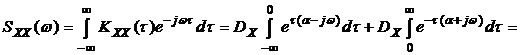
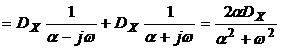. (3.7)

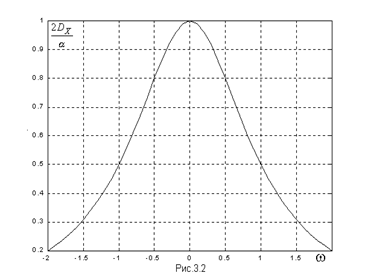
Зависимость спектральной плотности (3.7) от частоты w приведена на рис.3.2.

При решении ряда практических задач вместо преобразований Фурье над корреляционной функцией стационарного процесса целесообразно воспользоваться

двухсторонним преобразованием Лапласа. Такое преобразование можно получить на основе (3.2) и (3.3), положив в них :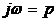

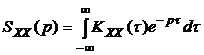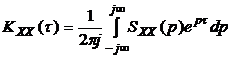, . (3.8)

Необходимость двухстороннего преобразования Лапласа вместо обычно применяемого при исследовании переходных процессов в контурах вызвано тем, что аргумент t меняется в пределах 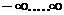, тогда как при одностороннем преобразовании Лапласа аргумент t изменятся от 0 до .

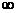Будем далее 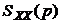называть операторной спектральной плотностью случайногопроцесса X(t). Для практического определения корреляционной функции при известной операторной спектральной плотности целесообразно воспользоваться теорией вычетов в полюсах, лежащих на комплексной плоскости p при t>0 слева от оси ординат (l_k,), а при t< 0 - справа от этой оси (m_k) [1,2]:

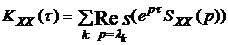при t>0; (3.9)

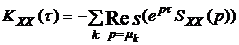при t<0. (3.10)

Аналогично могут быть определены и взаимные корреляционные функции:

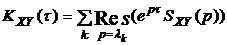при t>0; (3.11)

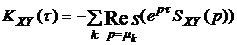при t<0. (3.12)

Операторную спектральную плотность, представляющую собой двухстороннее преобразование Лапласа над корреляционной функцией, можно выразить и через односторонние преобразования Лапласа:

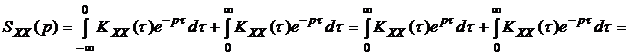
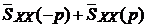= , (3.13)

где 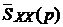- одностороннее преобразование Лапласа,

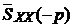- одностороннее преобразование Лапласа при замене p на –p.

Обратные преобразования в этом случае будут:

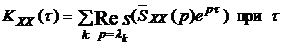>0, (3.14)

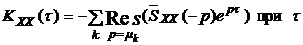<0. (3.15)

Если в выражение для спектральной плотности процесса (3.7) подставить 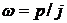, то

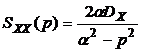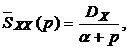
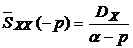, . (3.16)

Беря оригинал от 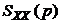при t>0 (полюс 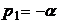), получим

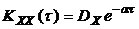(t>0).

При t<0 (полюс 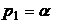), будем иметь

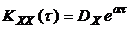(t<0).

Объединение полученных выражений для t>0 и t<0 дает известную аппроксимацию корреляционной функции:

.

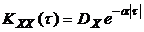ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СТАЦИОНАРНЫХ

СЛУЧАЙНЫХ ПРОЦЕССОВ

Постановка задачи

Задача анализа является прямой задачей; задача синтеза – обратной.

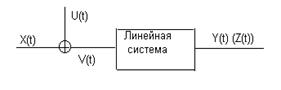Прямая задача. На вход системы поступает не только полезный сигнал X(t), но и помеха U(t) (рис.5.1).

Рис.5.1.

При решении задачи анализа заданы вероятностные характеристики процессов на входе системы (полезного и помехи), а также передаточная функция линейной системы. Требуется определить вероятностные характеристики ошибки на выходе, обусловленной зашумленностью полезного процесса.

Задача синтеза системы может быть решена при двух её постановках.

Во-первых, структура системы может быть задана и требуется определить её параметры, исходя из минимизации ошибки на выходе системы.

Во-вторых, требуется определить саму структуру линейной системы, при которой ошибка на выходе системы будет минимальна.

Её структуре

Покажем решение этой задачи на примере оптимизации параметров фильтра помехи при заданной его структуре (рис.4.1). Примем, что на вход системы помимо полезного процесса, характеризующегося математическим ожиданием m_X и корреляционной функцией 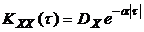, поступает также и помеха в виде так называемого белого шума с нулевым математическим ожиданием и корреляционной функцией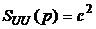 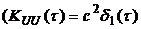). Поскольку для

схемы рис.4.1 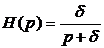, то согласно (5.7) 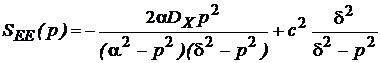. (5.8)

Беря оригинал от (5.8) при t>0, будем иметь:

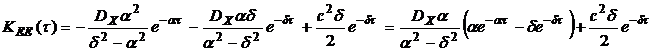Полагая в последнем выражении t=0, получим

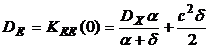. (5.9)

Из выражения (5.9) видно, что дисперсия зависит лишь от одного параметра контура рис.4.1. - d=1/RC=1/T (T – постоянная времени). Для определения величины параметра d, отвечающего минимальной дисперсии ошибки, необходимо выполнить два условия: 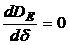и 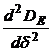>0 при D_E =min. Первое условие приводит к следующему выражению для d (второе условие при этом выполняется):

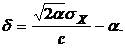(5.10)

При выполнении условия (5.10) дисперсия ошибки определится как:

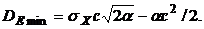
Рассматриваемая система является астатической - m_E=0.

К. П. КАДОМСКАЯ

ОСНОВЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ

Учебное пособие

для студентов курса и магистрантов факультета энергетики

Новосибирск

Кадомская К.П. Основы теории случайных процессов. Учебное пособие/Новосибирск: Изд-во НГТУ, 1999. – с.

В пособии рассматриваются основы теории случайных процессов, подкрепленные соответствующими примерами. Излагаются основные вероятностные характеристики случайных процессов, а также линейные и нелинейные их преобразования. Приводится методика оптимизации линейных систем, основанная на минимизации ошибок на их выходе. Даются краткие сведения из статистики случайных процессов.

Рецензент д-р техн. наук, профессор

В.З. Манусов

Работа подготовлена кафедрой техники и электрофизики высоких

напряжений

Новосибирский государственный

технический университет, 1999 г.

ОГЛАВЛЕНИЕ

Стр.

ПРЕДИСЛОВИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ СЛУЧАЙНЫХ

ПРОЦЕССОВ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.1. Случайные процессы и способы их характеристик . . . . . . . . .

1.2. Основные свойства математического ожидания и

корреляционной функции случайного процесса . . . . . . . . . . .

2. КЛАССИФИКАЦИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ. . . . . . . . . .

2.1. Стационарные процессы . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.2. Нормальные процессы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.3. Эргодические процессы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.4. Марковские процессы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ СТАЦИОНАРНЫХ

СЛУЧАЙНЫХ ПРОЦЕССОВ . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СТАЦИОНАРНЫХ

СЛУЧАЙНЫХ ПРОЦЕССОВ . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.1. Линейные операторы и их воздействия на случайные

процессы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.2. Линейные преобразования случайных процессов при исполь-

зовании понятия спектральной плотности . . . . . . . . . . . . . . . . .

5.ПРИМЕНЕНИЕ ТЕОРИИ СТАЦИОНАРНЫХ ПРОЦЕССОВ

К РЕШЕНИЮ ЗАДАЧ, СВЯЗАННЫХ С АНАЛИЗОМ И СИНТЕ-

ЗОМ ДИНАМИЧЕСКИХ СИСТЕМ . . . . . . . . . . . . . . . . . . . . . . . . . .

5.1. Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. .

5.2. Задача анализа динамической системы . . . . . . . . . . . . . . . . . . . .

5.3. Оптимизация параметров линейной системы при заданной

её структуре . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.4. Определение оптимальной линейной системы при незаданной

её структуре. Уравнение Винера-Хопфа и способ его решения

6. ВЫБРОСЫ СЛУЧАЙНЫХ ПРОЦЕССОВ . . . . . . . . . . . . . . . . . . . . .

6.1. Общие понятия. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.2. Математическое ожидание числа положительных выбросов . .

6.3. Математическое ожидание времени превышения процессом

X(t) заданного уровня . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7. НЕКОТОРЫЕ НЕЛИНЕЙНЫЕ ЗАДАЧИ ТЕОРИИ СЛУЧАЙНЫХ

ПРОЦЕССОВ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7.1 Метод статистической линеаризации . . . . . . . . . . . . . . . . . . . . . . .

…7.2. Исследование точности нелинейных систем . . . . . . . . . . . . . .. . .

8.ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ

ПО ДАННЫМ ОПЫТОВ . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . .. .

8.1. Статистическая оценка математического ожидания случайного

процесса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.2.Статистическая оценка корреляционной функции случайного

процесса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.3. Статистическая оценка спектральной плотности случайного

процесса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.4. Определение статистической оценки закона распределения

ординаты стационарного процесса . . . . . . . . . . . . . . . . . . . . . . . .

ЛИТЕРАТУРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

ПРЕДИСЛОВИЕ

Теория вероятностей возникла в XY111 веке и первое время развивалась как наука о событиях. С середины X1X века появились новые задачи, в которых требовалось не только устанавливать вероятность появления факта-события, но и необходимо было также установить, какие значения могли принимать те или иные случайные величины (СВ). СВ – это более общее понятие, включающее в себя понятие событий. Действительно, с каждым событием можно сопоставить случайную величину X=1, если событие происходит и X=0, если оно не происходит.

В 1827 году Р.Броуном было открыто хаотическое движение малых частиц, взвешенных в жидкости. Для описания этого явления понадобился аппарат, дающий возможность производить количественный анализ не случайных величин, а случайных процессов, протекающих во времени. Понятие случайных процессов (СП) или случайных функций (СФ) является обобщением понятия случайных величин, так как при определенном значении аргумента (времени) случайная функция является случайной величиной.

Так, например, случайным процессом является процесс изменения напряжения в какой-либо точке электрической сети под действием случайных изменяющихся во времени нагрузок в различных узлах этой сети.

В учебном пособии рассматриваются вероятностные характеристики случайных процессов и приводятся решения некоторых задач, связанных с анализом и синтезом динамических систем и выбросами СП. Даются краткие сведения из статистики СП.

При написании учебного пособия автор опирался на соответствующую главу из книги [1] и на опыт преподавания этого раздела курса теории вероятностей в Санкт-Петербургском и Новосибирском технических университетах.

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ СЛУЧАЙНЫХ

ПРОЦЕССОВ