Физическая интерпретация частотного коэффициента передачи оптимального фильтра.

Фильтр обеспечивающий выделение известного сигнала из смеси с «белым» шумом должен пропускать на выход гармонические колебания, частоты которых отвечают лишь тем участком спектра, где спектральная плотность полезного сигнала отлична от 0, при этом |K(ω)| должен быть пропорционален модулю спектральной плотности сигнала, т.е. тому вкладу в результирующий выходной сигнал, который вносится от того или иного участка спектра частот. Если спектр входного сигнала имеет дискретную структуру (например сигнал является периодическим), то изложенный выше принцип приводит к фильтрам с гребенчатой АЧХ широко применяемым в технике связи и радиолокации. Согласованный фильтр функционирует подобно

гребенчатому. Удается еще больше повысить вероятность обнаружения сигнала в виду целесообразного использования ФЧХ спектральной плотности сигнала. Сигнал на выходе согласованного фильтра достигает абсолютного максимального в момент времени t_o , когда все спектральные составляющие входного колебания складываются на выходе когерентно (синфазно) т.е. имея одни и те же фазовые сдвиги.

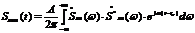
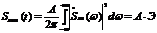где Э – энергия сигнала.

Таким образом эффект согласованной спектрации связан с коррекцией фазовых соотношений между отдельными спектральными составляющими сигнала.

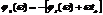Рассмотрим условие компенсации начальных фаз всех гармонических составляющих входного сигнала. Согласно этому условию оптимальный или согласованный фильтр должен иметь такую ФЧХ, чтобы фазовый сдвиг в ней - φ_Ѕ(ω) был равен по величине и противоположен по знаку начальной фазе составляющей спектра входного сигнала (S_вх(ω))

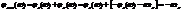Составляющие ФЧХ (-ωt_o) указывает на то, что пик выходного сигнала задержан относительно началам действия входного сигнала на время t_o.

19) Согласованный фильтр для прямоугольного видеоимпульса с длительностью U и τ

Вычислим спектральную плотность

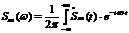
Находим коэффициент передачи согласованного фильтра:

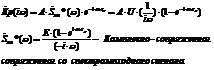
t_o = τ – максимум отклика на выходе приходящийся на момент окончания импульса.

U – амплитуда импульса;

A – постоянный коэффициент, имеющий размерность обратной спектральной плотности сигнала [A] = [1 / S(ω)]. Структурная схема согласованного (оптимального) фильтра. Структурная схема синтезируется по виду комплексногокоэффициента передачи К_Ф (iω).

Фильтр представляет собой каскадное соединение

3-х линейных звеньев:

1) масштабный усилитель с коэффициентом усиления А;

2) идеальный интегратор (интегрирующее звено) реализующего множитель (1 / iω).

3) устройство с коэффициентом передачи (1 – е ^-iωτ)

Реализуемого с помощью звена задержки сигнала на время τ, инвертораимеющего знак инвертора и сумматора. Передаточная функция звена задержки (идеальная линия задержки без потерь) равна е ^-iωτ

Отношение сигнал / шум:

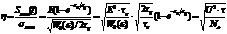
Квазиоптимальные фильтры

В ряде случаев удаётся получить достаточно эффективную фильтрацию сигналов из смеси с “белым ” шумом применив фильтры более простой конструкции по сравнению с оптимальными фильтрами. Рассмотрим RC 4-х полюсник, интегрирующего типа.

t_ц=R×C – постоянная времени. На входе одновременно действует “белый” шум. Поскольку данная цепь линейна, то прохождение сигнала и шума можно рассмотреть независимо. Максимальная полезность сигнала на выходе достигается в момент окончания импульса.

Отсюда максимальное отношение на выходе цепи:

Э=Е²×t_и - энергия сигнала, В²/Гц. Приняв во внимание, что энергия видеоимпульсов, получим:

Множитель в [ ] даёт величину проигрыша в отношении сигнал/шум по сравнению с оптимальным фильтром. Введя параметр

х=t /R×C=t /t_ц, получаем:

Из графика видно, что при х = 1,25 функция достигает максимума. Выбираем соответствующее значение постоянной времени RC цепи, можно создать весьма простой квазиоптимальный фильтр (почти оптимальный)

Отношение сигнал/шум, который лишь на 11% меньше чем в согласованном фильтре.

Квазиоптимальные фильтры с приёмными характеристиками удается создать только для относительно простых сигналов. Требования: пропустить без ослабления колебания из той области частот где сосредоточена основная доля энергии сигнала.

Теорема Котельникова

Реальные сигналы всегда имеют конечную длительность ограниченную полосу частот. Граничные частоты спектра определяются свойствами системы передачи и самим получателем. Например, при передачи дискретных сообщений полоса частот определяется скоростью передачи, а при передачи телевизионных изображений принятым стандартом четкости (числом строк). Для функции с ограниченным спектром В. А. Котельников доказал теорему лежащую в основе дискретизации непрерывных сигналов. Согласно этой теореме функция U(t), не содержащая частот выше F полностью определяется последовательностью своих отсчетов в моменты времени, отстоящие друг от друга на Δt≤1/2F. Восстановление осуществляется с помощью ряда Котельникова:

Выражение представляет разложение непрерывной функции U(t) в ряд по ортогональным функциям вида (sinx / x). Выражение U(kΔt), называется отсчетами функции U(t), а множитель называется функцией отсчетов. Если обозначим

τ = (t - kΔt), то множитель:

Функция ψ(τ)=1 в моменты времени t = kΔt и ψ(τ)=0, при

t = (k ± m)Δt, где m=1,2,3… Эта функция называется функцией отсчетов или координатным синусом. Ширина главного лепестка на нулевом уровне равна 1/F. Спектр функции отсчетов является равномерным в полосе (-F; F) и равен нулю вне этой полосы. Амплитуда спектра (модуль) S(f)=1/2F. Теорема Котельникова позволяет единым образом рассматривать передачу любого сигнала ( и дискретного и непрерывного) на передачу чисел. Эта теорема лежит в основе всех видов импульсной модуляции. Согласно этой теореме необходимая частота следования импульсов, называемая тактовой частотой F_i должна определяться из условия F_i≥2 F_в ,где F_в – верхняя граничная частота спектра передаваемого сообщения.

22. Принцип цифровой обработки сигналов. Переход к системам цифровой обработки сигналов является одной из основных тенденций современной техники связи. Это направление оказывает влияние на развитие теории и техники сигналов и систем.

Функциональная схема цифровой обработки континуального (непрерывного) сигнала.

Рисунок

Вначале входной сигнал s(t) подвергается дискретизации с помощью электронного ключа (ЭК), работающего с шагом Т. Сигнал на выходе ЭК имеет вид последовательности коротких импульсов s_T(t), являющихся отсчетами сигнала s(t). Предполагается, что при выборе шага Т на основании теоремы Котельникова обеспечивается сохранение информации, содержащейся в континуальном сигнале.

Каждый отсчет запоминается в интегрирующей схеме (ИС) на время t₃, необходимое для срабатывания АЦП. Очевидно, что t₃ < Т. На выходе ИС получается ступенчатое поле-банке s_T(t). ВАЦП уровень каждой ступени этого колебания измеряется (сравнивается с эталонным) и ему присваивается значение ближайшего квантованного уровня, общее число которых L = 2ⁿ (n - число разрядов кодового слова). Каждому уровню в АЦП ставится в соответствие кодовое слово - двоичное число, состоящее из n разрядов, каждый из которых представлен единицей или нулем (стандартным импульсом или паузой). Очевидно, что чем длинее кодовое слово, тем выше точность представления каждого отсчета сигнала. Полученный цифровой сигнал поступает в цифровой фильтр (ЦФ), представляющий собой вычислительное устройство. В ЦФ производится обработка кодовых слов по заданному алгоритму, использующему математические операции сложения, умножения на постоянные коэффициенты и задержки во времени. В качестве ЦФ может быть использована и универсальная ЭВМ (ПЭВМ). Среди разнообразных алгоритмов обработки цифровых сигналов наибольшее распространение получила цифровая фильтрация, включающая в себя цифровой спектральный анализ.

На выходе ЦФ возникают новые кодовые слова, соответствующие профильтрованному сигналу, и после прохождения ими ЦАП сигнал приобретает структурную форму, причем высота каждой ступени равна отсчету выходного сигнала в соответствующие моменты времени. Под выходным дискретизированным сигналом S_Tвых (t) подразумевается последовательность коротких импульсов, амплитуды которых равны высотам соответствующих ступеней. В 4-х полюснике называемом синтезирующим фильтром СФ осуществляется преобразование сигнала с выхода ЦАП в континуальный выходной сигнал S_вых (t). Одним из основных параметров системы является шаг дискретизации Т, задаваемый опорным генератором. Особое внимание уделяется повышению стабильности частоты 1/T этого генератора, задающего строгую синхронность управления всеми ключевыми элементами устройств системы. Цифровые системы обработки сигналов обладают рядом преимуществ по сравнению с аналоговыми: 1) абсолютная стабильность их характеристик;

2) в ЦФ возможна реализация таких алгоритмов обработки, которые в аналоговой обработке не реализуемы; 3) характеристики фильтра легко перестраиваются. Возможно создания адаптивных (самонастраивающихся) систем.

25. Разделение сигналов при передаче

Различные сигналы могут быть переданы в одной физической среде (линии связи), если имеется возможность их разделения на приемной стороне. Это возможно, если сигналы F_n(t) и F_m(t) при m ¹ n линейно независимы. Линейная независимость обеспечивается, если интеграл произведения G(t) этих сигналов равен нулю:

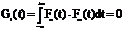(m¹n)

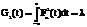(m = n)

где - некоторая конечная величина.

Сигналы отвечающие этому условию, называют ортогональными. Если в ансамбле (в наборе) сигналов каждая пара их взаимно ортогональна, то его называют системой ортогональных сигналов.

Рисунок

Временное разделение. Наиболее просто ортогональность любых по форме сигналов обеспечивается, если каждый из них передается в течение своего интервала времени, не перекрывающегося никаким другим.

Рисунок а). Например, при междугородних переговорах один и тот же канал связи может поочередно предоставляться различным абонентам. Сигналы, временные интервалы которых взаимно не перекрываются, подчиняются условию ортогональности. Так, для двух сигналов F₁(t) и F₂ (t) (рис. а)

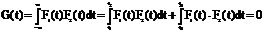
Рисунок

так как в интервале от t₁ и t₂ сигнал F₂(t) = 0 и в интервале от t₃ до t₄ сигнал F₁(t) = 0.

Частотное разделение. Каждое сообщение передается в непрерывающемся интервале частот (рис.) (d). Сигналы выделяются фильтрами. Практически реальные сигналы имеют бесконечные спектры, поэтому их можно делить только искусственным ограничением их спектра, а условие ортогональности выполняется приближенно.

Рассмотрим радиоимпульсы с длительностью t и различной частотой заполнения: 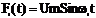при 0 < t < t (рис. в спектре его)

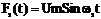
Интеграл от произведения этих сигналов:

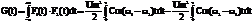
Учитывая выражение (1), можно утверждать, что если

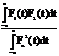<< 1 (где n = 1 или n=2), то сигналы приблизительно ортогональны. Практически это выполняется при условии (w₂ w₁) ³ 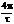. Смысл этого ограничения заключается в том, что при его выполнении спектры первых лепестков (рис. в) не перекрываются. При частотном разделении спектр сигнала переносится в необходимую область с помощью модуляции.

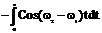
24. При частотном разделении сигналы различных каналов размещаются в неперекрывающихся частотных полосах. На приемном конце эти сигналы выделяются с помощью фильтров. Для размещения спектров нескольких НЧ сообщений в неперекрывающихся частотных полосах, необходимо, чтобы несущие колебания (переносчики) в различных каналах имели различные частоты. Эти колебания модулируются передаваемыми сообщениями по одному из параметров (амплитуде, частоте или фазе). Несущие частоты должны быть разнесены на интервал, равный ширине спектра модулированного колебания (рис. 2). При АМ интервал между несущими частотами должен равняться удвоенной ширине спектра НЧ сигнала (сообщения). Очевидно, наилучшее уплотнение по частоте можно получить при применении однополосной модуляции (ОМ).

Рисунок

В технике радиосвязи для частотного уплотнения каналов применяется двойная модуляция. Передаваемыми сообщениями модулируются поднесущие колебания с различными частотами f_k. Число поднесущих равно числу каналов. Сумма модулированных поднесущих образует групповой сигнал, которым затем модулируется несущая с частотой ƒ₀ >> f_k. На приеме вначале детектируется несущая и выделяется групповой сигнал. Затем при помощи фильтров из этого сигнала выделяются канальные сигналы, представляющие собой поднесущие, промодулированные передаваемыми сообщениями.

Детектированние канальных сигналов позволяет выделить сообщение на выходе каждого канала.

Системы с поднесущими широко применяются в РРЛ и телеметрии. Помехоустойчивость и эффективность систем с поднесущими зависит от вида модуляции как поднесущей, так и несущей. Возможный выбор здесь достаточно большой: АМ-АМ, АМ-ЧМ, ОМ-ЧМ, АМ-ФМ и т.д. Широко распространенная в РРЛ система ОМ-ЧМ обеспечивает сравнительно высокую помехоустойчивость при малом уровне помех. С увеличением индекса модуляции заметно снижается эффективность использования полосы частот. К недостаткам ОМ-ЧМ относятся наличие порога помехоустойчивости и появление переходных помех при многолучевом распределении радиоволн. Система ОМ-ОМ обеспечивает высокую эффективность, не имеет порога и свободна от переходных помех за счет многолучевости р/р/в. Многоканальная радиотелеграфическая связь применяется в КВ диапазоне. Обычно используется ЧМ-ОМ или ОФМ_Н-ОМ при небольшом числе каналов. На УКВ и в РРЛ для телеграфии выделяется часть телефонных каналов, которые уплотняются телеграфическими каналами.

23 При временном способе разделения все каналы занимают одну и ту же полосу частот, но линия связи используется поочередно для передачи канальных сигналов. Временное разделение применимо только в случае импульсной модуляции (рис. 3). При импульсной модуляции благодаря большой скважности между импульсами одного канала остается большой промежуток времени, в котором можно разместить импульсы других каналов.

Рисунок

Основу системы составляют два синхронно работающих коммутатора К₁ и К₂. На передающей стороне к ламелям коммутатора К₁ подводятся канальные сигналы от входных преобразователей. Вращающаяся щетка коммутатора К₁ поочередно подключает каждый из преобразователей на вход импульсного модулятора (ИМ), осуществляющего модуляцию импульсной последовательности, поступающей в него от генератора импульсов ГИ. Импульсы, модулированные сообщениями всех каналов, поступают в линию связи, а затем на коммутатор К₂, разделяющий каналы на приеме. Коммутатор К₂ подключает каждый входной преобразователь в момент, когда по каналу связи поступает импульс данного канала. Важно, чтобы коммутаторы К₁ и К₂ работали синхронно. Для синхронизации обычно передают вспомогательные синхронизирующие импульсы, для которых отводится один или несколько каналов. Применяют электронные коммутаторы. При ВРК применяют различные виды импульсной модуляции - ИКМ, ФИМ, ШИМ и др.