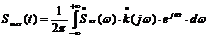Количественное определение информации. Энтропия и производительность дискретного источника сообщения

Количество информации 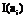, содержащееся в символе а_i, выбираемом из ансамбля 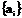( 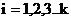), где k - объем алфавита, с вероятностью 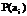,причем 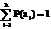,определяется по формуле:

I(a_i)=-log₂P(a_i).

Основание логарифма может быть произвольным, оно определяет лишь систему единиц измерения количества информации. Информация измеряется в двоичных единицах (битах). Одна двоичная единица информации – это количество информации, содержащейся в одном из двух выбираемых с равной вероятностью символов.

Энтропия источника независимых сообщений - среднее количество информации H(A), приходящейся на один символ выдаваемых дискретным источником независимых сообщений с объемом алфавита К, можно найти как математическое ожидание случайной дискретной величины I(a_i), определяющей количество информации, содержащейся в одном случайно выбранном символе а_i:

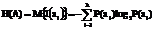.Если в единицу времени источник выдает в среднем V_u символов (скорость источника V_u) , то среднее количество информации, создаваемой источником в единицу времени Н(А)= V_u Н(А) = 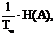где Т_ср - средняя длительность одного символа. Характеристику Н(А) называют производительностью дискретного источника. Источник называют стационарным, если описывающие его вероятностные характеристики не меняются во времени.

Свойства энтропии:

1) Энтропия является непрерывной или дискретной, неотрицательной функцией P(a_i)

2) Энтропия = 0 тогда и только тогда, когда вероятность одного из состояний источника равна1

3) Энтропия максимальна, когда все состояния источника равновероятны, т.е. P(a₁)= P(a₂)= P(a_i)=1/к

4) Энтропия сложного сигнала полученного объединением двух независимых сигналов равна сумме этих энтропий.

Причинами избыточности являются:

1) неравные вероятности появления знаков (символов) на выходе источника

2) наличие вероятностных связей между символами.

В теории вероятности доказывается, что при заданном числе возможных состояний, энтропия максимальна при равном распределении вероятностей р₁=р₂=…=р_к=1/к.

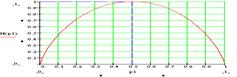
Для двоичного источника без памяти, когда к=2, энтропия максимальна при р(а₁)=р(а₂)=0.5 и равна log₂2=1 бит.

Зависимость энергии этого источника от р(а₁)=1-р(а₂) показана на рис. 1.

При р₂=0® р₁=1 ,а при р₂=1® р₁=0.

Энергия Н при этих значениях равна 0.

Помехи и искажения

Под помехой понимается воздействие накладываемое на сигнал, т.е. помеха это нежелательное изменение сигнала. Шум - случайная помеха. Помехи разнообразны как по своему происхождению так и по физическим свойствам. В радио каналах наиболее распространены атмосферные помехи от грозовых разрядов. Индустриальные помехи возникают из-за резкого изменения тока в цепях электроустройств. В проводных каналах основным видом помех являются импульсные шумы и прерывание связи. Когда помеха влияет на сигнал в виде x = s + n, такая помеха наз. аддитивной. Если же помеха

x = µ(t) s, то называется мультипликативной, n - шум,

µ(t) - случайный процесс. В реальных каналах имеют место обе помехи:

x = µ(t) s + n. Аддитивные делятся:

1) флуктуационные или гладкие

( распределённые по частоте или времени)

2) сосредоточенные по частоте (гармонические)

3) сосредоточенные по времени (импульсные).

Флуктуационный – это непрерывный во времени с гаусовским распределением, мгновенным значениям и нулевым математическим ожиданием. Энергетический спектр такой помехи n0 в пределах анализируемой полосы частот Δf полагают равномерным (помеха типа белого шума) Часто такую помеху полагают стационарной и эргодической. Гармоническая – это аддитивная помеха, энергетический спектр которой сосредоточен в сравнительно узкой полосе частот сопоставимой или даже более узкой, чем полоса сигнала. Импульсная- это аддитивная помеха представляющая собой последовательность импульсов, возбуждаемых кратковременным ЭДС апериодического или колебательного характера. Шум представляет собой случайную помеху. Источниками шума в электрических цепях могут быть флуктуация тока из-за дискретной природы носителей зарядов (электроны, дырки, ионы) - это “дробовой эффект” Наиболее распространенной причиной распространение шума является флуктуации из-за теплового движения носителей заряда в проводнике вызывающие случайную разность потенциалов на его концах. Квадрат эффективного напряжения теплового шума определяется формулой Найквиста: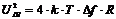

T-абсолютная температура которая имеет сопротивление R, Δf - полоса частот,

В реальном канале сигнал при передачи искажается и сообщение воспроизводится с некоторой ошибкой. Причинами ошибок являются искажения вносимые самим каналом и помехи. Частотные и временные характеристики канала определяют так называемые линейные искажения. Канал может вносить и нелинейные искажения обусловленные нелинейностью его звеньев. Линейные и нелинейные искажения обусловлены известными характеристиками каналов и в принципе могут быть устранены путем соответствующей коррекции. Помехи заранее известны и не могут быть полностью устранены.

8. Сигналы и их спектры (Спектральный анализ сигналов).

Сигналы представляют собой изменяющуюся во времени электрическую величину. Различают сигналы периодические и непериодические. Простейшие непериодические сигналы представляют собой одиночные импульсы произвольной длительности

Рисунок

Периодические - бесконечную временную последовательность импульсов одинаковой формы с равными периодами повторения s(t) = s(t + n T),

n = ± 1, ±2,…, T - период сигнала

Рисунок

Кроме временного, существуют и другие формы представления сигналов. При анализе сигналов и их прохождении по каналу связи удобнее применять частотное представление. Известно, что любую периодическую функцию фремени s(t) с помощью ряда Фурье можно представить в виде суммы гармонических составляющих

s(t) = 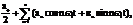где а₀/2 - постоянная составляющая s(t),

a_n, в_n - амплитуды косинусной и синусной составляющих ряда (коэффициенты ряда). Этот ряд может быть преобразован к виду:

s(t) = 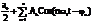где А_n - амплитуды гармонических составляющих ряда

A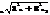

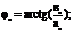
Амплитуды гармонических составляющих могут быть определены с помощью формул Эйлера для коэффициентов ряда Фурье:

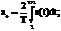
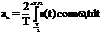; в_{n =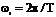} - основная частота последовательности, образующей периодический сигнал на интервале времени 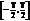. Гармонические составляющие ряда (1) графически представляются отдельными спектральными линиями А_n = f(w), разнесенными относительно начала координат на расстояния nw₁. Совокупность величин An называют спектром амплитуд. Спектр содержит бесконечное число гармоник, амплитуды An которых убывают в пределе до бесконечно малого значения. Спектр - дискретный (линейчатый). Для передачи сигнала без искажений необходимо по каналу связи передать все бесконечное число гармоник. Практически это невозможно, т.к. потребовался бы канал с ¥ большой полосой частот. Допускаются некоторые искажения формы сигнала, что позволяет ограничиться передачей конечного числа гармонических составляющих. Чем больше число гармоник передается, тем меньше искажения. Передают только часть гармоник, несущих основную энергию сигнала. Интервал на шкале частот, в котором размещается ограниченный спектр сигнала, называют шириной спектра. Кроме спектра амплитуд рассматривают также спектр фаз.

Выводы. 1. Спектральное представление сигналов - разложение его на сумму, конечную или бесконечную, элементарных гармонических сигналов с различными частотами. 2. Периодические сигналы можно представить с помощью рядов Фурье, которые образуются суммированием, вообще говоря, бесконечного числа гармоник с частотами, кратными основной частоте повторения последовательности. 3. Спектральное представление непериодических, в частности импульсных, сигналов осуществляется путем разложения их в интеграл Фурье. 4. В частотной области сигнал характеризуется своей спектральной плотностью. 5. Сигнал и его спектральная плотность связаны взаимно парой преобразований Фурье.

9, Спектр периодического сигнала. Ширин а спектра.

Рассмотрим разложение в ряд Фурье периодической последовательности прямоугольных видеоимпульсов с известными параметрами (t, Т, А), четной относительно точки t = 0

Рисунок

В технике связи отношение 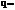называют скважностью последовательности. Для четкой функции коэффициенты ряда Фурье равны ;

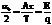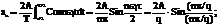
в = 0 отсюда приходим к следующему ряду Фурье

s(t) =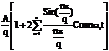

Рисунок

При 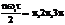и т.д. Sin 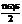обращается в "0" и соответствующие гармоники также будут равны нулю. При 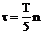обращаются в "0" 5, 10, 15 и т.д. гармоники. Действительно для 5-ой гармоники (n = 5)

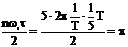a_n=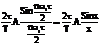

10, Спектр непериодического сигнала. Ширин а спектра. Спектральная плотность. Спектр непериодического сигнала определяют, используя интеграл Фурье 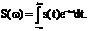Сигнал s(t) и его спектральная плотность S(w) взаимно-однозначно связаны прямым и обратным преобразованием Фурье S(t) =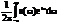 Непериодический сигнал можно рассматривать как периодический с периодом Т 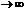. При этом разность частот между соседними гармониками стремиться к нулю. Спектр становится сплошным, амплитуды - бесконечно малыми. Спектральная плотность сигнала S(w) - комплексная величина, ее можно представить в виде

S(w) = A(w) + i B(w) = S(w) e 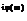, где

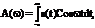
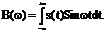
Модуль и фаза спектральной плотности S(w) = 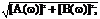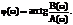Структура спектра непериодического сигнала полностью определяется спектром амплитуд S(w) и спектром фаз 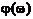(это и есть спектральная плотность).

Спектральная плотность прямоугольного видеоимпульса амплитудой V, длительностью 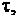симметричного относительно начала отсчета времени: на основании (3)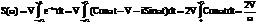

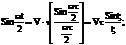где

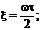
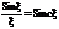координатный синус или функция отсчета. Значение спектральной плотности на нулевой частоте равно площади импульса S(o) = V 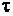. Спектральная плотность обращается в нуль при 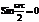или при 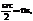где n = 1,2,3…; т.у. при w= 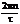.График отсчетной функции Рисунок

Необходимую ширину спектра Dw выбирают предельно малой, но такой, чтобы в ней была сосредоточена основная энергия сигнала (30% в первом лепестке). Энергия может быть определена согласно равенству Парсеваля

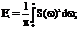
Dw» 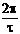; D¦_(Гц)» Этим выражением пользуются для оценки ширины спектра, в общем случае D¦ = , где К - некоторый коэффициент К ³ 1. Короткий импульс имеет широкий спектр , а длинный импульс - узкий спектр. Это общее положение, согласно которому ширина спектра любого процесса обратно пропорциональна его длительности. При t®0 импульс вырождается в дельта - функцию d(t), спектр которой является равномерным (белый шум).

Выводы. (результаты, резюме):1. Спектральное представление сигналов - разложение его на сумму, конечную или бесконечную, элементарных гармонических сигналов с различными частотами. 2. Периодические сигналы можно представить с помощью рядов Фурье, которые образуются суммированием, вообще говоря, бесконечного числа гармоник с частотами, кратными основной частоте повторения последовательности. 3. Спектральное представление непериодических, в частности импульсных, сигналов осуществляется путем разложения их в интеграл Фурье. 4. В частотной области сигнал характеризуется своей спектральной плотностью. 5. Сигнал и его спектральная плотность связаны взаимно парой преобразований Фурье.

11) Спектральный метод исследования прохождения сигналов через линейные цепи.

Под линейностью понимается свойство системы не образовывающее гармонических колебаний на выходе, т.е. на выходе линейной цепи не могут присутствовать гармоники с частотами которых не было на входе если на вход линейного сигнала подать одно гармоническое колебание с известной частотой, амплитудой начальной фазы, то на выход должно быть тоже одно гармоническое колебание той же частоты, но возможно с другой амплитудой и начальной фазой. По изменению амплитуды гармоники можно судить о степени затухания гармонического колебания в этой системе. А по изменению начальной фазы о скорости распространения сигнала в ней. Если для какого-то конкретного сигнала известна функция, показывает изменение затухания и скорости распространения гармоники со всеми возможными частотами, эта функция является адекватной математической модели этой системы в частотной области. Она называется комплексным коэффициентом передачи системы:

К(jω) = | К(jω)| e ^jφ(ω), где

| К(jω)| - АЧХ,

φ(ω) – ФЧХ. АЧХ характеризует передаточное свойство системы по амплитуде, АЧХ показывает для каждого конкретного значения ω_j отношение амплитуды гармоники этой частоты на выходе системы к амплитуде гармоники этой же частоты на входе. Полоса частот в пределах которой АЧХ изменяется от своего максимального значения до 0,707 называется полосой пропускания системы. Если коэффициент передачи системы остается постоянным для всех частот, то такая система считается идеальной и коэффициент передачи становится не функцией частоты, а постоянной коэффициентом усиления/ослабления системы. Данный коэффициент говорит об изменении масштаба сигнала без изменения его формы при прохождении сигнала через эту систему. ФЧХ для каждого конкретного значения ω_j показывает набег фазы гармоники этой частоты за время прохождения через систему. Она характеризует скорость распространения гармоники в системе. Поскольку набег фазы прямо пропорционален значению частоты ω_j

умножению на время распространения гармоники в системе:

φ(ω) = Δt_jω_j. Если скорость распространения гармоник всех частот в системе одинакова, то набег фазы каждой гармоник будет прямо пропорционален значению частоты этой гармоники, т.к. Δt_j=const для всех частот и ФЧХ такой системы будет иметь вид наклонной прямой линии. Чем меньше угол наклона идеальная и реальная ФЧХ относительно оси абсцисс, тем выше скорость распространения гармоник в этой системе. Гармоники более высокой частоты распространяются быстрее в рассматриваемой системе и затухание сильнее по сравнению с НЧ компонентами. Подобные характеристики имеют отрезок телефонного кабеля определенной длины. Суть спектрального метода анализа линейных систем заключается в выражении:

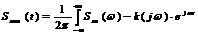
По известному входному сигналу находят с помощью прямого преобразования Фурье его спектральной плотности. Спектр выходного сигнала находят перемножением входного сигнала и комплексного коэффициента передачи системы:

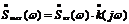
а затем по известному спектру выходного сигнала находят его форму с помощью обратного преобразования Фурье: