Определение касательных напряжений при изгибе.

При поперечном изгибе кроме нормальных напряжений в поперечном сечении бруса возникают касательные напряжения, а согласно закону парности, такие же напряжения появляются и в продольных сечениях бруса.

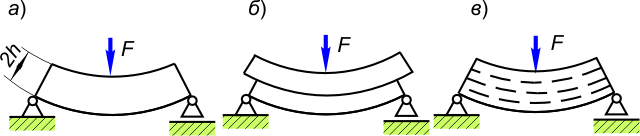Рисунок 1

Возникновение касательных напряжений в продольных сечениях можно проиллюстрировать таким примером. Если брус прямоугольного сечения высотой 2 h нагрузить силой F, он изогнется, как показано на рис.1, а. Если из такого же материала изготовить два бруса высотой h каждый, то при нагружении их силой F и отсутствии трения между ними они изогнутся каждый сам по себе (рис. 1, б). Отсюда видно, что при изгибе целого бруса высотой 2h между частями бруса, разделенными продольными слоями, возникает взаимодействие, в результате которого и возникают касательные напряжения (рис. 1, в).

Касательное напряжение в любой точке поперечного сечения (рис. 2) определяется, как и парное напряжение, возникающее в продольном сечении, по формуле Журавского;

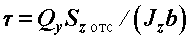
где 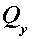- поперечная сила в рассматриваемом сечении;
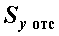- статический момент относительно нейтральной оси поперечного сечения той его части, которая расположена по одну сторону от прямой KL, проведенной параллельно нейтральной оси через исследуемую точку;
b - ширина поперечного сечения на уровне исследуемой точки;
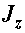- момент инерции всего сечения относительно нейтральной оси.

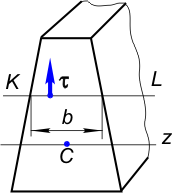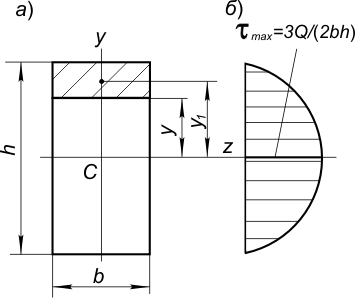Рисунок 2	Рисунок 3

В основу вывода формулы Журавского положено допущение о равномерном распределении касательных напряжений по ширине сечения.

Применим формулу Журавского к прямоугольному поперечному сечению бруса (рис.3, а), в котором возникла поперечная сила 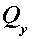. Момент инерции прямоугольного сечения 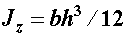, ширина сечения, b=const по всей высоте. Следовательно, касательные напряжения 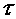в точках сечения, расположенных на расстоянии у от центральной оси, зависят от изменения статического момента 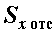заштрихованной части сечения выше уровня у.
Статический момент заштрихованной части сечения 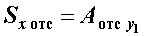, где заштрихованная площадь 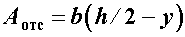, а ордината центра тяжести этой площади 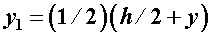. Следовательно,
.
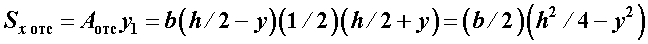Подставив найденные значения 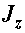, 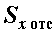в формулу , получим
.
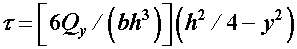Как видим, эпюра касательных напряжений по высоте сечения (рис. 3, б) изображается квадратной параболой. Максимальное напряжение возникает в точках сечения, расположенных на центральной оси (при

у = 0): .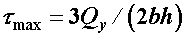
Таким образом, максимальное касательное напряжение в 1,5 раза превышает среднее значение напряжения 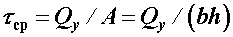. У верхней и нижней кромки сечения (при у = h/2) .
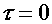Поскольку при переходе от верхней кромки сечения к нижней касательное напряжение изменяется по параболическому закону, деформация сдвига 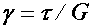тоже изменяется по этому закону. Поэтому при поперечном изгибе поперечные сечения бруса не остаются плоскими, а искривляются (рис. 4).

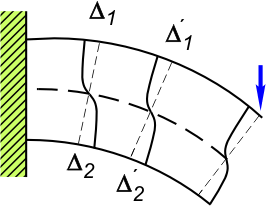Рисунок 4

При постоянном значении Q по длине бруса поперечные сечения претерпевают одинаковые искажения: 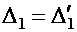и 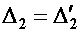. Следовательно, искривления поперечных сечений не сказываются на законе распределения нормальных напряжений и их значений. В балке прямоугольного и круглого сечений максимальные касательные напряжения возникают в тех точках, где нормальные напряжения равны нулю (на нейтральной оси), и, наоборот, в крайних точках сечения, где нормальные напряжения максимальны, касательные напряжения равны нулю. Поэтому за опасные можно принять точки, наиболее удаленные от нейтральной оси, что подтверждается практикой эксплуатации балок, работающих на изгиб. Однако в случае тонкостенных профилей (например, двутавра) необходимо проверить прочность балки и в точках, где полка сочленяется со стенкой, поскольку здесь возникают значительные как нормальные, так и касательные напряжения.

45)Закон распределения касательных напряжений по высоте типовых сечений балок.

Данный вопрос я не нашелL