В каких пределах допустима надежная работа материала?
Отношение предельного напряжения 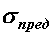 к расчетному
к расчетному 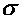 называется коэффициентом запаса прочности
называется коэффициентом запаса прочности 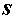 :
: 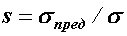 .
.
При расчете элемента конструкции коэффициент запаса прочности задается заранее. Задаваемый заранее коэффициент запаса называется нормативным или допускаемым и обозначается 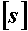 .
.
Прочность элемента конструкции обеспечивается, если действительный коэффициент запаса прочности не ниже допускаемого, т.е. 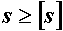 .
.
Это неравенство выражает условие прочности элемента конструкции.
Разделив предельное напряжение на нормативный коэффициент запаса, получим допускаемое напряжение 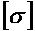 :
: 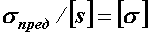 .
.
Тогда условие прочности можно выразить неравенством 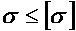 , т. е. прочность элемента конструкции обеспечивается, если наибольшее напряжение, возникающее в нем, не превышает допускаемого.
, т. е. прочность элемента конструкции обеспечивается, если наибольшее напряжение, возникающее в нем, не превышает допускаемого.
Для пластических материалов как при растяжении, так и при сжатии предельным напряжением является предел текучести 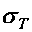 . Поэтому для них допускаемое напряжение получают, исходя из предела текучести
. Поэтому для них допускаемое напряжение получают, исходя из предела текучести 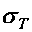 :
: 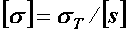 , причем в этом случае
, причем в этом случае 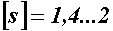 .
.
33 31 вопросы действительно одинаковые, так как они несут один и тот же смысл.
34) Чистый сдвиг. Формулы для определения напряжений.
Сдвигом называют такой вид деформации, когда в поперечных сечениях возникают только перерезывающие силы. Такое напряженное состояние соответствует действию на стержень двух равных противоположно направленных и бесконечно близко расположенных поперечных сил (рис. 2.13, а, б), вызывающих срез по плоскости, расположенной между силами.
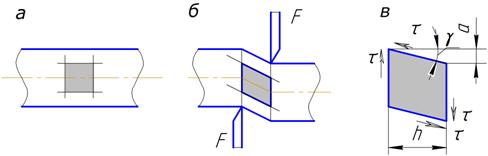
Рис. 2.13. Деформация и напряжения при сдвиге
Срезу предшествует деформация – искажение прямого угла между двумя взаимно-перпендикулярными линиями. При этом на гранях выделенного элемента (рис. 2.13, в) возникают касательные напряжения. Величина 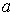 смещения граней называется абсолютным сдвигом. Значение абсолютного сдвига зависит от расстояния h между плоскостями действия сил F. Более полно деформацию сдвига характеризует угол
смещения граней называется абсолютным сдвигом. Значение абсолютного сдвига зависит от расстояния h между плоскостями действия сил F. Более полно деформацию сдвига характеризует угол 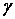 , на который изменяются прямые углы элемента – относительный сдвиг:
, на который изменяются прямые углы элемента – относительный сдвиг:
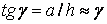 . (2.27)
. (2.27)
Используя ранее рассмотренный метод сечений, легко убедиться, что на боковых гранях выделенного элемента возникают только перерезывающие силы Q=F, являющиеся равнодействующими касательных напряжений:
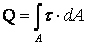 . (2.28)
. (2.28)
Принимая во внимание, что касательные напряжения распределены равномерно по поперечному сечению А, их значение определяется соотношением:
 . (2.29)
. (2.29)
Экспериментально установлено, что в пределах упругих деформаций величина касательных напряжений пропорциональна относительному сдвигу (закон Гука при сдвиге)
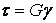 , (2.30)
, (2.30)
где G – модуль упругости при сдвиге (модуль упругости второго рода).
Между модулями продольной упругости и сдвига существует взаимосвязь
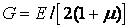 ,
,
где 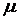 – коэффициент Пуассона.
– коэффициент Пуассона.
Приближенные значения модуля упругости при сдвиге, МПа: сталь – 0,8·105; чугун – 0,45·105; медь – 0,4·104; алюминий – 0,26·105; резина – 4.
