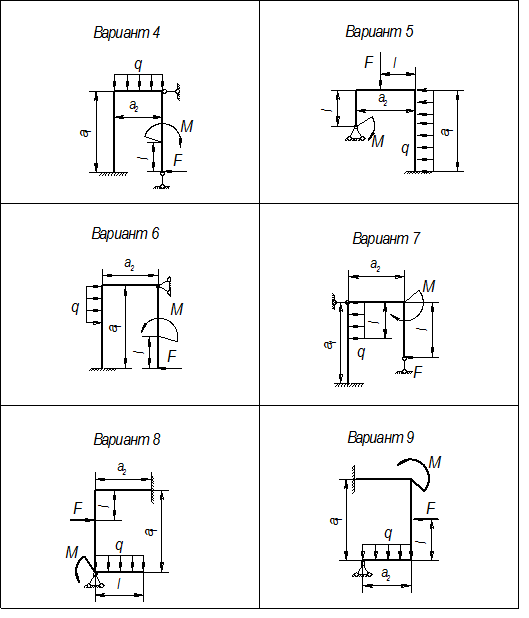
Задача № 1 Расчет на прочность при сложном сопротивлении
Для стальной пространственной стержневой конструкции требуется подобрать поперечные сечения элементов из условия прочности. Для элемента I подобрать диаметр круга, для элемента II – размеры прямоугольного сечения b и h (отношение h/b – взять из табл. 1), предварительно рационально его расположив. Для элемента III провести проверку прочности, исходя из того, что II и III элементы изготовлены из единого прутка.
План решения:
Для каждого элемента пространственной конструкции необходимо:
1. построить эпюры внутренних силовых факторов;
2. определить положение опасного сечения;
3. установить вид деформации в опасном сечении;
4. найти положение опасных точек в опасном сечении;
5. определить вид напряженного состояния в опасных точках;
6. записать условие прочности и определить размер поперечного сечения элемента (для III элемента провести проверку прочности), приняв 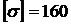 МПа.
МПа.
Примечание. Первая цифра варианта обозначает вариант схемы, вторая – вариант линейных размеров, третья – вариант нагрузок (табл. 1). Длина всех элементов пространственной конструкции одинакова и равна 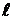 . При решении задачи руководствоваться алгоритмом расчета на прочность в условиях сложного сопротивления.
. При решении задачи руководствоваться алгоритмом расчета на прочность в условиях сложного сопротивления.
Таблица 1
| 1. Варианты линейных размеров | 2. Варианты нагрузок | ||||||||||
| № вар. | 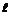 , м , м | 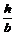 | № вар. | 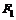 , кН , кН | 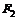 , кН , кН | 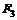 , кН , кН | 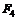 , кН , кН | 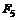 , кН , кН | 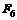 , кН , кН | 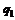 , кН/м , кН/м | 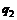 , кН/м , кН/м |
| 0,6 | 1,5 | 5,0 | 2,0 | 5,0 | -3,0 | 1,0 | – | – | 2,0 | ||
| 0,7 | 1,5 | – | 1,5 | – | -2,5 | 2,0 | 3,0 | 3,0 | – | ||
| 0,8 | 1,7 | 2,0 | 3,0 | 3,0 | 4,0 | 1,0 | – | 1,0 | – | ||
| 0,9 | 1,8 | – | 2,0 | – | 5,0 | 3,0 | -2,5 | 2,5 | 1,0 | ||
| 1,0 | 1,9 | 3,0 | 3,0 | 2,0 | 3,0 | – | – | 2,0 | – | ||
| 0,6 | 2,0 | – | 2,5 | – | 5,0 | -4,0 | -4,0 | 2,0 | 2,5 | ||
| 0,7 | 1,6 | 2,0 | 3,0 | 2,0 | 4,0 | – | – | – | -2,5 | ||
| 0,8 | 1,7 | – | 3,5 | – | -2,5 | 3,0 | 3,0 | 3,0 | -3,0 | ||
| 1,0 | 1,8 | 3,0 | 2,4 | 2,5 | 5,0 | 2,0 | 2,0 | 1,0 | – | ||
| 0,9 | 1,5 | – | 2,0 | – | -2,0 | -2,5 | – | 2,0 | 2,6 |
| Расчетные схемы пространственных конструкций к задаче № 1 |
| Вариант 0 |
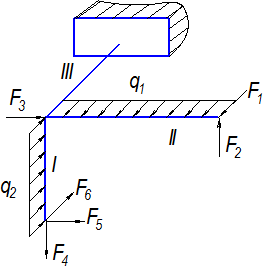 |
| Вариант 1 |
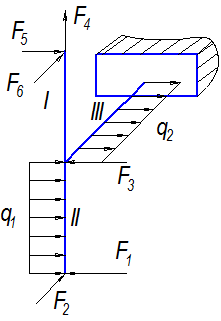 |
| Вариант 2 |
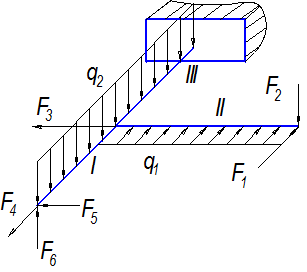 |
| Вариант 3 |
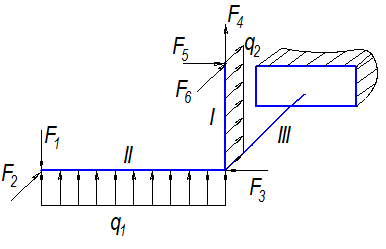 |
| Вариант 4 |
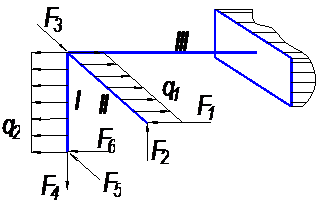 |
| Вариант 5 |
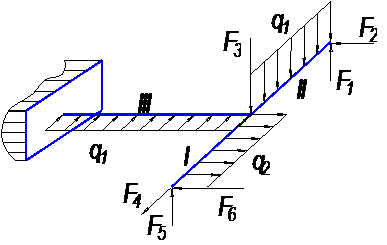 |
| Вариант 6 |
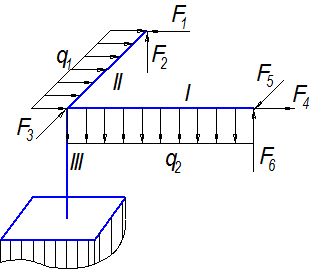 |
| Вариант 7 |
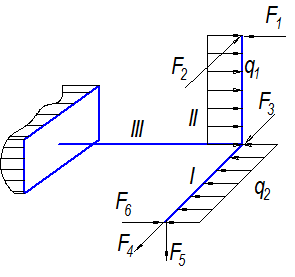 |
| Вариант 8 |
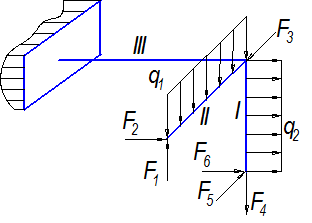 |
| Вариант 9 |
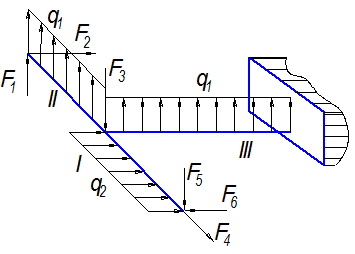 |
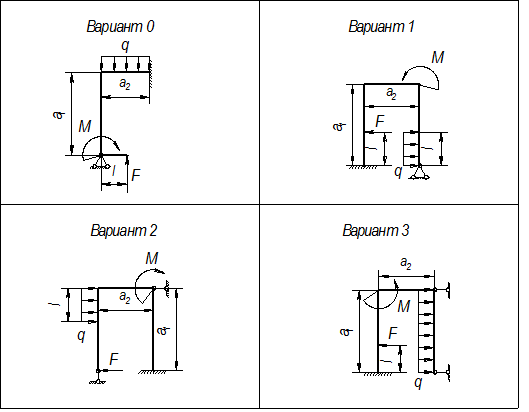
Задача № 2 Расчет на прочность и жесткость статически неопределимых рам
Для данной по варианту статически неопределимой рамы подобрать рациональное поперечное сечение из условия прочности и проверить конструкцию на жесткость, если материал стержней рамы – Ст. 3: 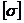 =160 МПа, Е=
=160 МПа, Е= 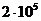 МПа. Жесткость сечений всех участков рамы постоянна: ЕIх=const.
МПа. Жесткость сечений всех участков рамы постоянна: ЕIх=const.
План решения
1. Раскрыть статическую неопределимость рамы методом сил.
2. Построить эпюры изгибающих моментов и продольных сил для заданной системы и провести проверку правильности решения.
3. Установить положение опасного сечения рамы и из условия прочности подобрать рациональное сечение.
4. Определить прогиб в месте предполагаемой наибольшей деформации, показав приближенный вид упругой линии рамы, и записать условие жесткости.
Примечание. Первая цифра варианта обозначает вариант схемы, вторая – вариант линейных размеров, третья – вариант нагрузок (табл. 2). При решении задачи рекомендуется использовать алгоритм метода сил.
Таблица 2
| 1. Вари-анты схем | 2. Варианты линейных размеров | 3. Варианты нагрузок | |||||||||
| № вар. | № вар. | 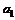 , м , м | 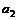 , м , м | 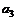 , м , м | 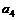 , м , м | 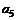 , м , м | 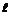 , м , м | № вар. | 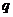 , кН/м , кН/м | 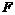 , кН , кН | 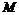 , кНм , кНм |
| 1,5 | 2,0 | 0,6 | 2,0 | 1,9 | 0,5 | ||||||
| 2,0 | 1,8 | 0,7 | 2,2 | 1,6 | 0,4 | ||||||
| 1,2 | 1,6 | 1,0 | 2,4 | 2,6 | 0,6 | ||||||
| 1,8 | 1,4 | 0,8 | 2,5 | 2,0 | 1,0 | ||||||
| 1,4 | 1,2 | 0,5 | 2,3 | 2,4 | 0,3 | ||||||
| 1,7 | 1,9 | 0,7 | 2,1 | 1,6 | 1,0 | ||||||
| 1,6 | 1,7 | 0,9 | 2,0 | 1,8 | 0,4 | ||||||
| 1,9 | 1,5 | 0,6 | 1,8 | 1,8 | 0,6 | ||||||
| 1,3 | 1,3 | 0,8 | 2,0 | 2,6 | 0,8 | ||||||
| 2,0 | 1,2 | 0,6 | 1,8 | 2,4 | 0,5 |
Расчетные схемы статически неопределимых рам к задаче № 2