Назначение теорий предельного состояния

Для того, чтобы сравнивать два неодинаковых напряженных состояния, введем для них некоторые характеристики.

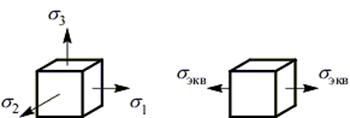
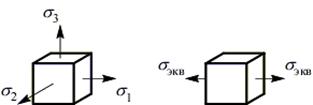
1. Напряженные состояния подобны (однотипны), если их главные напряжения пропорциональны. Значит, два напряженных состояния однотипны, если

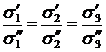
2. Напряженное состояние, при котором наступает недопустимый процесс (для хрупких материалов – разрушение, а для пластичных – появление недопустимых остаточных деформаций), называется предельным (опасным) напряженным состоянием. Произвольное напряженное состояние можно довести до предельного путем пропорционального и одновременного увеличения его главных напряжений. Обозначим 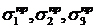– главные напряжения предельного напряженного состояния.

3. Запасом прочности n данного напряженного состояния называется число, показывающее, во сколько раз одновременно и пропорционально надо увеличить его главные напряжения, чтобы оно стало предельным:

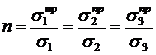(2.6)

4. Напряженные состояния элементов из одного и того же материала равнопрочны, если у них равны запасы прочности.

Для определения запаса прочности любого напряженного состояния по (2.6) надо знать значения главных напряжений предельного напряженного состояния, ему подобного, которые могут быть найдены только экспериментально.

Практически этого сделать нельзя по двум основным причинам:

– во-первых, в настоящее время отсутствуют машины, позволяющие создавать произвольные напряженные состояния;

– во-вторых, если бы такие машины и были, то невозможно провести неограниченно большое число опытов по определению значений главных напряжений предельных напряженных состояний при их произвольном отношени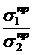и:

и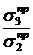

Поэтому о прочности данного напряженного состояния судят по прочности напряженного состояния, ему не подобного, путем высказывания предположения об их равнопрочности.

Предположение о равнопрочности разнотипных напряженных состояний называется теорией или гипотезой прочности.

Обычно данное напряженное состояние сравнивают с одноосным растяжением, для которого значения предельных механических характеристик материала 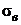и 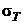определяются просто.

Одноосное напряженное состояние, равнопрочное данному, называется эквивалентным. Обозначим 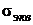– главное напряжение эквивалентного напряженного состояния.

На основании сформулированного предположения (критерия) равнопрочности устанавливается зависимость между 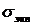и :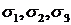

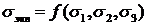
Опасной называется точка элемента системы, в которой 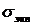по одной из теорий прочности достигает наибольшего значения, и условие прочности тогда можно записать в виде:

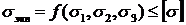
Сформулировать универсальный критерий равнопрочности, учитывающий всю совокупность причин, практически влияющих на прочность (тип напряженного состояния, состояние материала, характер действия на тело внешних факторов) до сих пор не удалось. Поэтому, в настоящее время при расчете на прочность используется несколько теорий прочности, взаимно дополняющих друг друга. Теории прочности, объясняющие возникновение предельного состояния разрушением, называются теориями хрупкого разрушения, а объясняющие его возникновение появлением недопустимых пластических деформаций – теориями пластичности.

Рассмотрим классические теории предельного состояния, высказывающие гипотезы о характере функции .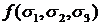

Теории хрупкого разрушения

Первая теория прочности – теория наибольших нормальных напряжений (теория Галилея).

Критерий равнопрочности: напряженных состояния равнопрочны по хрупкому разрушению, если у них равны наибольшие нормальные напряжения

.

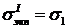Условие прочности при растяжении

.

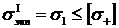Также можно использовать условие прочности для сжатия

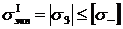. (2.7)

Данная теория нашла подтверждение только для весьма хрупких материалов (камень, бетон, кирпич). Ее основным недостатком является неучет двух главных напряжений.

Вторая теория прочности – теория наибольших линейных деформаций (теория Мариотта).

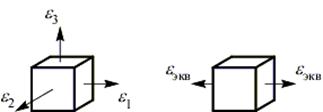
Критерий равнопрочности: напряженных состояния равнопрочны по хрупкому разрушению, если у них равны наибольшие линейные относительные деформации

.

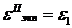Согласно закону Гука, при одноосном напряженном состоянии

.

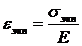Наибольшую линейную относительную деформацию при произвольном напряженном состоянии запишем, используя обобщенный закон Гука:

.

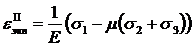Приравнивая правые части, получим эквивалентное напряжение по второй теории

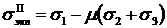. (2.8)

Вторая теория применима только для хрупких материалов, в том числе для хрупких металлов.

Теории пластичности

Третья теория прочности – теория наибольших касательных напряжений (теория Кулона).

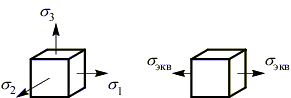
Критерий равнопрочности: напряженных состояния равнопрочны по наступлению недопустимых пластических деформаций, если у них равны наибольшие касательные напряжения

.

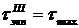По формуле (2.2) касательное напряжение в случае плоского напряженного состояния определяется как:

,

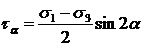из которой следует, что

.

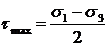При одноосном напряженном состояни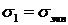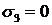и , , и

.

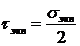Приравнивая правые части полученных выражений, получим эквивалентное напряжение по третьей теории

.

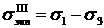Для случая плоского напряженного состояния, когда нормальное напряжение на одной из площадок равно нулю (изгиб с кручением), выразив главные напряжения через напряжения на произвольной площадке, условие прочности принимает вид:

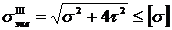. (2.9)

Третья теория используется при расчете элементов конструкций, изготовленных из пластичных материалов. Ее недостатком является неучет главного напряжения σ₂.

Четвертая теория прочности – теория удельной потенциальной энергии формоизменения – энергетическая теория (теория Мизеса – Генки).

Критерий равнопрочности: напряженные состояния равнопрочны по наступлению недопустимых пластических деформаций, если у них равны удельные потенциальные энергии формоизменения:

.

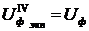Используя приведенное в разделе 8.1.5 выражение для потенциальной энергии изменения формы (8.1) для одноосного и объемного напряженного состояния, получим

,

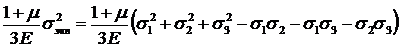откуда эквивалентное напряжение по четвертой теории

.

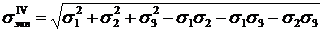Для случая плоского напряженного состояния ( ):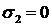

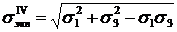. (2.10)

Выражая главные напряжения через напряжения на произвольных площадках для плоского напряженного состояния, когда на одной из площадок нормальное напряжение равно нулю, получим:

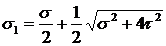и .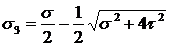

Подставляя полученные выражения в формулу (8.6), условие прочности можно записать в виде:

.

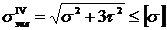Энергетическая теория хорошо согласуется с экспериментальными данными (лучше, чем третья теория), и широко используется для пластичных материалов.

Универсальная теория Мора

Пятая теория прочности – теория предельных состояний (теория Мора).

Критерий равнопрочности: напряженные состояния равнопрочны по наступлению предельного состояния, если при одновременном пропорциональном увеличении главных напряжений их круги Мора одновременно коснутся предельной огибающей.

Если изобразить в координатах t-s семейство кругов Мора для различных предельных состояний материала, то огибающая этого семейства будет предельной огибающей для данного материала.

Изобразим в координатах t-s три предельных круга Мора:

- круг с центром в точке O₁ – для случая одноосного сжатия (главные напряжения σ₁ = 0, σ₂ = 0, σ₃ = σ_вс);

- круг с центром в точке O₂ – для случая одноосного растяжения (главные напряжения σ₁ = σ_вр, σ₂ = 0, σ₃ = 0);

- круг с центром в точке O₃ – для случая плоского напряженного состояния (главные напряжения σ₁, σ₃).

Линия C₁D₁, огибающая круги, называется предельной огибающей.

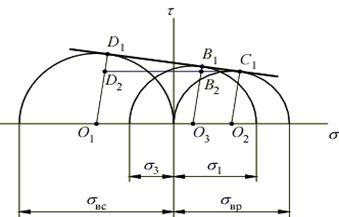
Как видно из рисунка, 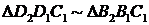, то есть

.

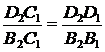Запишем длины отрезков через соответствующие напряжения:

,

,

,

.

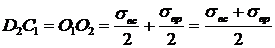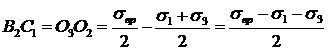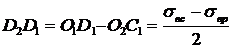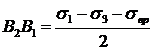Подставляя эти значения в пропорцию, получим

,

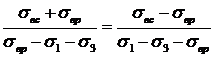откуда:

.

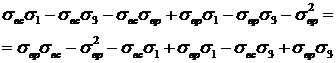После сокращения имеем

,

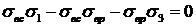тогда

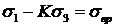, где .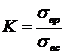

Т.к. 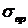– предел прочности для одноосного растяжения, его можно заменить .

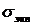Таким образом, эквивалентное напряжение по теории Мора, равно:

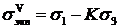. (2.11)

Для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию, 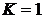, следовательно

,

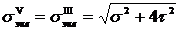то есть теория Мора совпадает с теорией максимальных касательных напряжений.

Для хрупких материалов 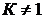, и

.

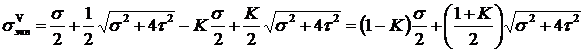Интересно, что для весьма хрупких материалов с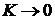

,

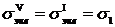то есть теория Мора совпадает с теорией максимальных нормальных напряжений.

Теорию Мора рекомендуется использовать для хрупких (в том числе анизотропных) материалов вместо первой и второй теорий. Ее недостатком является неучет промежуточного главного напряжения σ₂.

Общий случай нагружения

Сочетание изгиба в двух плоскостях с растяжением (сжатием) и кручением называется общим случаем нагружения.

Рассмотрим алгоритм расчета на прочность в общем случае нагружения на примере консольной балки прямоугольного поперечного сечения, изготовленной из пластичного материала:

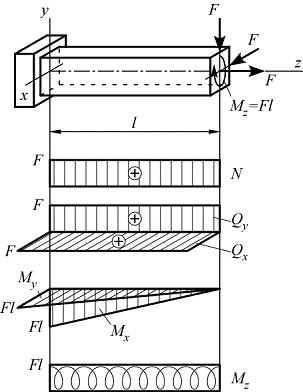
На рисунке показаны эпюры распределения внутренних силовых факторов вдоль оси балки.