Рекуррентные формулы построения канонического разложения случайной функции.

Рассмотренный в п.п. 5.5.3 способ построения координатных функций требует нахождения собственных чисел и собственных векторов корреляционной матрицы К. В случае большого n эта задача становится сама по себе достаточно сложной. Для ее упрощения приходится идти на отказ от оптимальных координатных функций (5.51) и использовать более простые функции. Рассмотренный ниже метод построения координатных функций основан на процедуре ортогонализации Грамма- Шмидта [ 7 ] и впервые разработан для достаточно общего случая В.С. Пугачевым.

Построение координатных функций 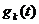и коэффициентов представлений 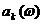осуществляется в этом методе последовательно.

Определим величину 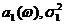и функцию 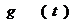формулами :

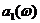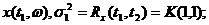= (5.58)

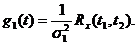
Функция 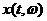будет после этого шага представлена у нас в виде

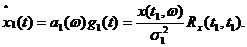(5.59)

Определим далее величины 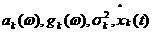по формулам:

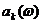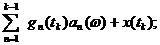= (5.60)

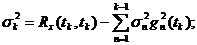(5.61)

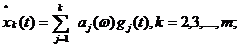(5.62)

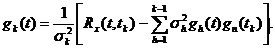(5.63)

Последовательность 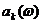, , 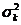, 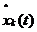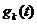при начальных условиях (5.52) - (5.53) определяет рекуррентный метод построения канонического разложения случайной функции. Заметим, что погрешность 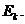Для этого способа превышает погрешность (5.57), однако в силу простоты этот способ часто используется на практике. При 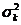= 0 процедура, вообще говоря, не определена. В этом случае целесообразно очередную точку 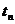заменить на другую, для которой 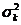≠ 0. Если такой точки не находится, это может говорить о том, что каноническое разложение построено.

Л И Т Е Р А Т У РА

1. ГУРМАН В.Е. Теория вероятностей и математическая статистика.

Учеб. Пособие для втузов. Изд. 5 – е, перераб. И доп. М.: Высшая школа, 1977.

2. Дж. Х. ЛЭНИНГ и Р.Г. БЭТТИН. Случайные процессы в задачах авто-матического управления. Пер. с англ. Под ред. В.С. Пугачева. М.: Ин. Лит., 1958.

3. Д. КОКС, Н. ЛЬЮИС. Статистический анализ последовательностей событий. Пер. с англ. Под редакцией Н.П. Бусленко. М.: Мир, 1969.

4. ФЕРРАРИ Д. Оценка производительности вычислительных систем.

Пер. с англ. А.И. Горлина, Ю.Б. Котова и Л.В. Ухова. Под ред. В.В.Мартинюка.

М.: Мир, 1981.

5. ФЕЛЛЕР В. Введение в теорию вероятностей и ее приложения.

Пер. с англ. Л.Р. Добрушина, А.А. Юшкевича и С.А. Молчанова. Под редакцией Е.Б. Дынкина. Изд. 2 – е. М.: Мир, 1967.

6. ПУГАЧЕВ В.С. Теория случайных функций. Изд. 2 – е, перераб. И доп. М.: ГИФМЛ, 1960.

7. ДЕМИДОВИЧ Б.П., МАРОН И.А. Основы вычислительной математики. Под ред. Б.П. Демидовича. М.: ГИФМЛ, 1960.

С О Д Е Р Ж А Н И Е

Стр

ВВЕДЕНИЕ ……………………………………………………………. 3

1.ОБЩИЕ СВОЙСТВА СЛУЧАЙНЫХ ПРОЦЕССОВ ФУНКЦИЙ И СЛУЧАЙНЫХ ПРОЦЕССОВ.

1.1. Определение случайных функций…………………………………..4

1.2. Моменты конечномерных распределений случайных

функций……………………………………………………………….5

1.3. Основные типы случайных функций и случайных процессов…..8

2.ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ

2.1. Примеры дискретных случайных процессов в АСУ…………….14

2.2. Цепи Маркова………………………………………………………15

2.3. Классификация состояний Марковских цепей…………………..18

2.4. Эргодические свойства непериодических цепей. Стационарное

распределение………………………………………………………………20

3. ПУАССОНОВСКИЕ ПРОЦЕССЫ

3.1. Примеры пуассоновских процессов в АСУ………………………21

3.2. Дифференциальноные уравнения для переходных вероятностей………………………………………………………………..24

3.3. Процесс чистого размножения…………………………………….25

3.4. Пуассоновские процессы в системах массового обслуживания…………………………………………………………...….26

4. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ

НЕПРЕРЫВНЫМ ВРЕМЕНЕМ

4.1. Свойства корреляционных функций случайных процессов с

непрерывным временем……………………………………………30

4.2. Сложение случайных процессов…………………………………..31

4.3. Дифференцируемость выборочных функций случайного

процесса……………………………………………………………………..32

4.4. Интегрирование случайных процессов……………………………35

5. ПРЕДСТАВЛЕНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ И СЛУЧАЙНЫХ

ФУНКЦИЙ

5.1 Методы описания детерминированных функций…………………………………………………………………..38

5.2 Представление случайных процессов на конечном интервале

времени………………………………………………………………...…40

5.3 Интегральные уравнения с корреляционной функцией в качестве

ядра.............................................................................................................41

5.4 Разложение случайных функций в ряд Карунена-Лоэва………………………………………………………………………...43

5.5 Канонические представления случайных функций……………………………………………………………………..47

ЛИТЕРАТУРА…………………………………………………………………...52