Интегральные уравнения с корреляционной функцией в

Качестве ядра

Для того, чтобы равенство (5.15) было справедливым, необходимо выполнение условия

(5.16)

в этом случае нетрудно видеть, что

где =

Уравнение (5.16) называется интегральным уравнением функции, превращающие (5.16) в тождество, называются собственными функциями, а - собственными значениями интегрального уравнения. Функция 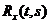называется ядром интегрального уравнения [6].

В п. п. 4.1 было показано, что 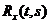симметрична и неотрицательно определена. Интегральные уравнения с симметричными, положительно определенными ядрами обладают целым рядом интересных свойств, основные из которых мы перечислим, отсылая за доказательствами к литературе [6].

Свойство 1.Существуют, по крайней мере, одна интегрируемая в квадрате функция 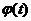и одно действительное число , которые удовлетворяют условию (5.16).

Свойство 2.Из выражения (5.16) следует, что если - решение уравнения, то и есть также решение. Поэтому всегда можно выбирать так, что

(5.17)

Свойство 3.Собственные функции, соответствующие различным собственным значениям, являются ортогональными, т. е.

(5.18)

Свойство 4. Существует не более чем счетное множество собственных значений, и все они ограничены.

Свойство 5.Неотрицательно определенное, симметричное ядро интегрального уравнения (5.16) может быть разложено в ряд

(5.19)

где сходимость, равномерная для (это свойство называется теоремой Мерсера и играет важную роль в задачах представления случайных процессов).

Свойство 6. Собственные функции интегрального уравнения с симметричным неотрицательно определенным ядром образуют полный ортонормированный ряд.

Свойство 7.

(5.20)

Из последнего свойства в предположении, что при , следует также,

Свойство 8.Собственные числа действительны и с ростом 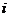не возрастают.

Отмеченные свойства интегральных уравнений гарантируют, что для любого случайного процесса второго порядка всегда можно построить ряд функций { }, обеспечивающий некоррелированные коэффициенты разложения.

Разложение случайных функций в ряд Карунена-Лоэва

Рассмотрим теперь вопрос о сходимости ряда:

(5.21)

где { }- собственные функции интегрального уравнения (5.16):

= (5.22)

где 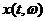- случайный процесс с корреляционной функцией .

Пусть в разложении (5.21) -конечно, тогда равенство (5.21) является приближенными почти для любой выборочной функции

(5.23)

где - случайный процесс.

Вычисляя

И так как (свойство 7)

то (5.25)

или

(5.26)

но и ограничена, а Отсюда следует, что

Определение 5.1.

Разложение случайного процесса в ряд (5.21) по собственным функциям интегрального уравнения (5.16) называют разложением Карунена-Лоэва. Оно обеспечивает представление случайного процесса посредством некоррелированных случайных величин Полезность разложения Карунена-Лоэва объясняется следующими двумя обстоятельствами:

1) во многих задачах теоретического анализа случайных функций разложение используется в качестве математического инструмента. В большинстве таких задач собственные функции и собственные значения не входят в окончательный результат, что позволяет не находить в явном виде;

2) в задачах, связанных с практическим применением, для получения удовлетворительного по точности результата достаточно знания одной или нескольких собственных функций и собственных чисел.