Методы описания детерминированных функций

Простейший способ представить детерминированный процесс заключается просто в задании всех или некоторого ряда значений сигнала . Другим распространенным способом представления детерминированного процесса является определение его в виде ряда или интеграла Фурье. В ряде случаев детерминированный процесс удобно представить в виде разложения в ряд по некоторой ортонормированной (или линейно-независимой) системе функций, отличной от тригонометрической. И, наконец, иногда детерминированные процессы удобно характеризовать в виде аналитического решения системы линейных дифференциальных уравнений.

Аналогичные способы представлений могут быть развиты для случайных процессов. Выбор того или иного способа определяется в первую очередь целью, которую преследует представление сигнала , и конкретными видами множеств

Рассмотрим функцию x(t) которая определена на интервале /0,Т/ (рис. 6).

Рис. 6. Выборочная реализация случайного процесса

Предполагаем, что интервал имеет конечное значение. В этом случае, если -некоторая полная система ортогональных на отрезке (0,Т) функций, x(t)можно представить в виде

(5.1)

где (5.2)

-коэффициент Фурье разложения x(t) по системефункций [6].

Поскольку практически можно использовать только конечное число коэффициентов, то желательно знать, чему равняется ошибка приближения, возникающая за счет учета конечного числа членов в сумме (5.1).

Ошибка представления x(t) при учете функций равна

(5.3)

Её удобно характеризовать интегралом

(5.4)

Известно, что если система функций полная [6], то

для любого конечного силу ортонормированности функций

(5.5)

где

Коэффициенты характеризуют вклад компоненты в разложение (5.1). Равенство (5.5) называется равенством Парсеваля [6].

В силу (5.5) любую функцию, удовлетворяющую условию , можно сколь угодно точно приблизить конечным числом функций. А это означает, что непрерывную функцию времени можно сколь угодно точно описать с помощью конечного набора чисел .

Частным случаем системы является широко распространенная система тригонометрических функций. Ряд (5.1) в этом случае называется рядом Фурье и имеет вид

, (5.6)

(5.7)

(5.8)

(5.9)

Теорема Парсеваля в этом случае принимает вид

(5.10)

Коэффициенты характеризуют вклад гармоники частоты в среднюю мощность сигнала x(t)и называются интенсивностью сигнала на этой частоте, а график величин в зависимости от называется линейчатым спектром Фурье.

Представление случайных процессов на конечном

Интервале времени

Пусть 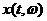, - случайный процесс, такой, что . Предположим, что 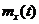=0, и пусть - полный ортонормированный набор функций, и что для почти любой выборочной функции существует предел суммы

(5.11)

где = (5.12)

Обычный предельный переход в (5.11) использовать нельзя, так как он требует, чтобы каждая выборочная функция могла быть представлена таким образом.

Отмечая, что правая часть (5.11) при разных представляет собой случайные величины (5.13)

Коэффициенты 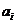ряда (5.13) представляют собой случайные величины со следующими характеристиками:

(5.14)

При каждом конечном ряд (5.13), разумеется, лишь приблизительно описывает выборочную функцию. Система случайных коэффициентов характеризуется вектором средних значений А и ковариационной матрицей с элементами

Использование представления (5.13) становится особенно удобным, если функции таковы, что ковариационная матрица имеет диагональный вид, т. е.

(5.15)

при при .