Данные об отказах электронной вычислительной машины

(в условных единицах).

	Номер отказа
Момент отказа
Номер отказа
Момент отказа
Номер отказа
Момент отказа

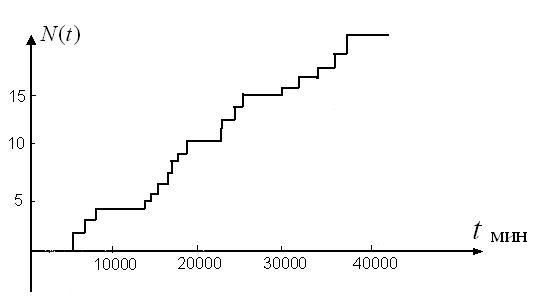
Рис.4. данные об отказах вычислительной машины. Накопленное

число отказов в зависимости от времени.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ПЕРЕХОДНЫХ

ВЕРОЯТНОСТЕЙ

В рассмотренных примерах для решения практических задач достаточно ограничиться анализом числа событий M (∆ τ), произошедших за произвольный, но фиксированный промежуток времени ∆ (t). Очевидно, что M (∆t) будет случайной величиной, принимавшей значения 0, 1, 2, … .

Пусть 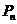(∆t) есть вероятность того, что M(∆t) = n. В частности, 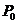(∆t) есть вероятность того, что не произойдет ни одного события, а (1- 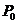(∆t)) – вероятность того, что произойдет хотя бы одно событие.

Предположим , что при ∆t → 0

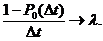(3.1)

где ∆t = t ₁ − t _2, λ - положительная постоянная.

Будем полагать, что распределение 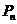(∆t) не зависит от t _{1 ,} т.е. процесс однородный во времени. Тогда выражение (3.1) является производной величины

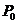(∆t) при ∆t = 0. Для малого интервала длины n вероятность одного или большего числа событий равна

1 - 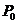(n) = λ h + 0 (h),

где через 0 (h) обозначена величина, убывающая быстрее, чем h .

Предположим, что выполнены следующие условия какого бы ни было число событий в период времени (0, t), условная вероятность того, что в течение интервала времени (t, t + h) произойдет событие, равна λ h а вероятность того, что произойдет более чем одно событие, равна 0 (h).

Однородный процесс, удовлетворяющий введенным предположениям, называется процессом Пуассона [5].

Из условия (3.1) легко вводится система дифференциальных уравнений для Рn (t). Для их вывода рассмотрим два смежных интервала (0, t) и (t, t+ h). Если n ≥ 1, то в интервале (0, t + h) может произойти ровно n событий тремя взаимно исключающими друг друга способами:

ни одного события за время (t, t+ h) и n событий за время (0, t);

одно событие за время (t, t+ h) и (n - 1) событие за время (0, t);

m ≥ 2 событий за время (t, t+ h) и (n - m) событий за время (0, t).

В соответствии с нашими предположениями вероятность первой из возмож- ностей равна произведению P_n (t) на вероятность того, что в интервале (t, t+ h) не произойдет ни одного события.

Вероятность того, что в интервале (t, t+ h) не произойдет события, равна

1- λ h – 0 (h). Вторая возможность имеет вероятность имеет вероятность

Р_n-1(t) ∙ λ h + 0, h и, наконец, вероятность третьей возможности убывает быстрее, чем h. Суммируя рассмотренные вероятности возможных изменений, можно получить

Р_n (t+ h) = Р_n (t) (1- λ h) + Р_n-1 (t) λ h + u (h). (3.3)

Это выражение можно записать в виде

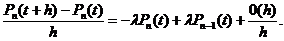
Устремляя 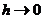, получим, что

Р'_n (t) = – λ Р_n (t) + λ Р_n-1(t) , n ≥ 1 (3.4)

при n = 0 вероятности второй и третьей возможности равны нулю и выражение (3.4) имеет вид

Р'₀ (t) = – λ Р₀ (t). (3.5)

Выражение (3.5) является обыкновенным дифференциальным уравнением первого порядка, а его решение для Р₀ (t = 0) =1 имеет Р₀ (t) = e ^{- λ t}.

Подставляя e ^{- λ t} в выражении (3.4), для n =1 получим дифференциальное уравнение для вероятности Р₁ (t). Аналогично можно найти члены уравнения (3.4) для n >1.

Для уравнений (3.4) - (3.5) ясен смысл параметра λ, он характеризует интенсивность событий , связанных с процессом Пуассона.

Вероятность Р₁ (t) равняется λ t e ^{- λ t}. Эта вероятность характеризует при Р₀ (t = 0) =1 вероятность наступления события к моменту времени t. Аналогично для n >1 получим

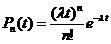(3.6)

- вероятность того, что при Р₀ (t = 0)= 1 за время t произойдет ровно n событий.

Распределение (3.6) является распределением Пуассона [ 1 ].

Процесс чистого размножения

Предположим, что в процессе Пуассона вероятность одного события за время (t, t+ h) зависит от числа событий за время (0, t ). Такой процесс можно рассматривать как пуассоновский процесс с переменной интенсивностью, характеризующейся последовательностью λ_0, λ₁, λ₂, ……

Удобной формой описания процесса Пуассона является описание его в пространстве состояний.

Пусть на время (0, t ) произошло n событий. Будем говорить, что в этом случае система находиться в состоянии E _n. Если за время h произойдет очередное событие, то система перейдет в состояние E _n+1. В противном случае система останется в состоянии E _n.

Определение 3.1.

Пуассоновский процесс, для которого переход из состояния E _n возможен только в состоянии E _n+1, называется процессом чистого размножения [ 5 ].

Если в момент t система находиться в состоянии E _n (n = 0,1, 2, ….), то вероятность того, что за время (t, t+ h) осуществляется переход в E _n+1, как это следует из (3.2 ), равна λ _n h + 0 (h). Вероятность иных изменений имеет более высокий порядок малости, чем h.

Дифференциальные уравнения (3.4 ) и (3.5 ) имеют для процессов чистого размножения следующий вид:

Р' _n (t) = – λ _n Р _n (t) + λ _n-1Р_n-1(t);

Р₀ (t) = – λ ₀ Р ₀ (t) (n ≥ 1 ) (3.7 ) Начальным состоянием системы является E ₀ , причем Р ₀ (0) =1, а Р ₀ (t) = e ^{- λ} ₀^t.

Можно, однако, в начальный момент времени рассматривать систему в любом состоянии.

Обобщим рассмотренный процесс размножения. С этой целью предположим, что в системе возможны переходы из E _n но только в E _n+1, но и в состояние E _n-1 . Конечно, в этом случае состояние E _n уже нельзя трактовать как число событий, реализованных на отрезке ( 0,t ).

Процесс такого вида впервые был изучен в биологии, где с его помощью опи-сывались процессы рождения и гибели. Поэтому иногда такие процессы называют процессами " гибели и размножения" [ 5 ].

В задачах анализа и синтеза АСУ такие процессы находят достаточно широкое применение. Поэтому рассмотрим их подробнее.