Вероятность совместного наступления двух независимых событий равна произведению вероятностей этих событий.

Р(АВ) = Р(А) × Р(В)

Доказательство:

Р(АВ) = Р(А) × РА(В) = Р(А) × Р(В).

Вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий.

Р(А₁ × А₂ × . . . × А_n) = Р(А₁) × Р(А₂) × . . . × Р(А_n).

Если события А₁, А₂, …, А_n независимы в совокупности, причем Р(А₁) = р₁, Р(А₂) = р₂, … , Р(А_n) = p_n, и в результате испытания могут наступить все события, либо часть из них, либо ни одного из них, то вероятность наступления события А, состоящего в появлении хотя бы одного из событий А₁, А₂, …, А_n, равна разности между единицей и произведением вероятностей противоположных событий 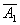, ,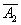…, 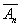: Р(А) = 1 –q₁q₂…q_n.

В частности, если все n событий имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий равна Р(А) = 1 -qⁿ.

Формулы полной вероятности и Байеса.

Формула полной вероятности

Пусть событие А может наступить в результате появления одного из событий Н1, Н2, …,Нn, которые образуют полную группу. Эти события будем называть гипотезами.

Теорема: Полная вероятность события А равна сумме парных произведений всех гипотез, образующих полную группу на соответствующие условные вероятности события А, т.е.

Р(А) =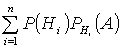

Доказательство:

Р(А) = Р(Н₁ А + Н₂ А + …+ Н_n А) = Р(Н₁ А) + Р(Н₂ А) + …+ Р(Н_n А) = Р(Н₁ )Р_H1 (А) + Р(Н₂ )Р_H2 (А) + Р(Н_n )Р_Hn (А).

Формула Байеса

Если событие А в результате испытания произошло, то возможно переоценить вероятность гипотез Н_i, образующих полную группу, по формуле Бейеса:

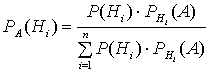, где Р(Н_i) – вероятность гипотезы, РА­(Н_i) – вероятность гипотезы Н_i после переоценки, при условии, что событие А уже произошло; Р_Hi­(А) – условная вероятность события А при выполнении гипотезы Н_i .

Доказательство.

Для получения искомой формулы запишем теорему умножения вероятностей событий А и Н_i в двух формах:

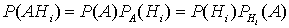откуда 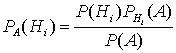или с учетом формулы полной вероятности 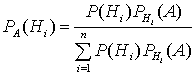. Эта формула называется формулой Байеса.

Схема Бернулли проведения испытаний. Биноминальная вероятность.

Формула Бернулли

Пусть производится серия n независимых испытаний, при чем в каждом отдельном испытании вероятность наступления события постоянна – р и отлична от 1 и нуля (т.е. 0 < р < 1), а не вероятность наступления событий - q.

Определим вероятность того. Что событие наступает m раз и не наступит n –m раз. Один из этих случаев запишется

× = .

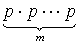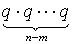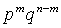Но таких сложных событий будет сколько можно составить сочетаний из n элементов по m. И поэтому искомая вероятность запишется:

Р_n(m) = 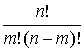p^mq^n-m

Итак, если в серии n независимых испытаний вероятность наступления события в каждом отдельном испытании постоянна и равна р, то вероятность того, что событие наступит m раз вычисляется по формуле Бернулли (1).

Полученная формула Бернулли на практике используется лишь при n < 10, а при n ® ¥ ее можно заменить другими. Выбор формулы зависит от значений p и q.