Вероятность невозможного события равна нулю.
4. Сумма вероятностей противоположных событий равна единицы, т.е.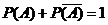 
Частостью называется отношение числа исходов, в которых событие появилось, к общему числу проведенных испытаний. Обозначается: W(A) =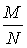 
, (1.2) где М – число исходов, в которых событие появилось или частота; N – число всех исходов испытания.
Статистическое определение вероятности
Проводится серия статистических наблюдений, N – количество наблюдений, M – число появления события А (M £ N).
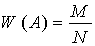- относительная частота появления события А.
Если в различных сериях наблюдений относительные частоты меняются мало, т.е. обладают свойством устойчивости, то можно ввести понятие вероятности.
Статистической вероятностью события А называется число, около которого группируются устойчивые значения относительных частот:
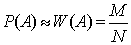
Иначе: Статистической вероятностью события называется предел частости при неограниченном увеличении числа испытаний.
Статистическое определение вероятности относится не к любым случайным событиям, а только к тем из них, которые обладают определенными свойствами.
Рассматриваемые события должны быть исходами только тех испытаний, которые могут быть воспроизведены неограниченное число раз при одних и тех же условиях.
События должны обладать так называемой статистической устойчивостью, или устойчивостью относительных частот. Это означает, что в различных сериях испытаний относительная частота (частость) события изменяется незначительно (тем меньше, чем больше число испытаний), колеблясь около постоянного числа.
Число испытаний, в результате которых появляется событие А, должно быть достаточно велико, ибо только в этом случае можно считать вероятность события Р(А) приближенно равной ее относительной частоте.
Геометрическое определение вероятности
Одним из недостатков классического определения вероятности, ограничивающим его применение, является то, что оно предполагает конечное число возможных исходов испытания.
Оказывается, иногда этот недостаток можно преодолеть, используя геометрическое определение вероятности, т.е. находя вероятность попадания точки в некоторую область (отрезок, часть плоскости и т.п.).
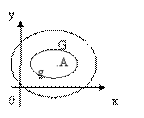
Рисунок 1.1
Пусть, например, плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу бросается точка. Это означает, что все точки области G «равноправны» в отношении попадания туда брошенной случайной точки. Полагая, что вероятность события А – попадание брошенной точки на фигуру g – пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g, найдем Р(А)=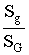 
, где Sg и SG – соответственно площади областей g и G (рисунок 1.1). Фигуру g называют благоприятствующей событию А.
Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (прямая, отрезок) и трехмерной (некоторое тело в пространстве). Обозначая меру (длину, площадь, объем) области через mes, приходим к следующему определению.
Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области, т.е. P(A)=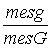 
.