Необходимые и достаточные условия экстремума.
Необходимое условие экстремума может быть сформулировано следующим образом: для того чтобы функция y=f(X) имела экстремум в точке x0, необходимо, чтобы ее производная в этой точке равнялась нулю ( 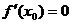 ) или не существовала.
) или не существовала.
Точки, в которых выполнено необходимое условие экстремума, т.е производная равна нулю или не существует, называются критическими (или стационарными). Критическая точка вовсе не обязательна являться точкой экстремума.
Первое достаточное условие экстремума. Теорема. Если при переходе через точку x0производная дифференцируемой функции меняет свой знак с плюса на минус, то точка x0 есть точка максимума функции y=f(x), а если с минуса на плюс, - то точка минимума.
Схема исследования функции у=f(x) на экстремум:
1. Найти производную 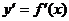 .
.
2. Найти критические точки функции, в которых производная 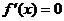 или не существует.
или не существует.
Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
Найти экстремумы функции.
Второе достаточное условие экстремума. Теорема. Если первая производная 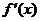 дважды дифференцируемой функции равна нулю в некоторой точке x0, а вторая производная в этой точке
дважды дифференцируемой функции равна нулю в некоторой точке x0, а вторая производная в этой точке 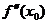 положительна, то x0 есть точка минимума функции
положительна, то x0 есть точка минимума функции 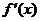 ; если
; если 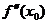 отрицательна, то x0-точка максимума.
отрицательна, то x0-точка максимума.
Схема исследования функции у=f(x) на экстремум:
1. Найти производную 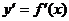 .
.
2. Найти критические точки функции, в которых производная 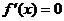 или не существует.
или не существует.
3. Найти вторую производную 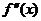 и определить ее знак в каждой критической точке.
и определить ее знак в каждой критической точке.
Найти экстремумы функции.
Третий достаточный признак экстремума. Если в критической точке функции f(x) обращаются в нуль не только первая производная f /(x0), но и все последовательные производные до ( 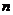 — 1)-й включительно [f'(x0) = =f"(x0) = …=f(n-1)(x0)=0],a производная n-го порядка существует, непрерывна и отлична от нуля
— 1)-й включительно [f'(x0) = =f"(x0) = …=f(n-1)(x0)=0],a производная n-го порядка существует, непрерывна и отлична от нуля 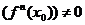 , то точка х0 будет точкой экстремума, если n — число четное, и не будет ею при n нечетном.
, то точка х0 будет точкой экстремума, если n — число четное, и не будет ею при n нечетном.
Характер экстремума при n четном определяется знаком f(n)(x0): максимум при f(n)(x0) <0, минимум при f(n)(x0)>0
35. Функции двух переменных: основные понятия, предел функции двух переменных, непрерывность ыункции двух переменных.
Определение: Пусть задано множество 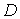 упорядоченных пар чисел
упорядоченных пар чисел 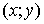 . Соответствие
. Соответствие 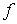 , которое каждой паре чисел
, которое каждой паре чисел 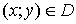 сопоставляет одно и только одно число
сопоставляет одно и только одно число 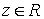 , называется функцией двух переменных, определенной на множестве
, называется функцией двух переменных, определенной на множестве 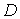 со значениями в
со значениями в  , и записывается в виде
, и записывается в виде 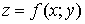 или
или 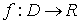 . При этом
. При этом 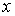 и
и 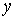 называются независимыми переменными (аргументами), а
называются независимыми переменными (аргументами), а 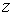 - зависимой переменной (функцией).
- зависимой переменной (функцией).
Множество 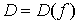 называется областью определения функции. Множество значений, принимаемых
называется областью определения функции. Множество значений, принимаемых 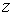 в области определения, называется областью изменения этой функции, обозначается
в области определения, называется областью изменения этой функции, обозначается 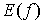 или
или 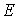 .
.
Определение: Функцию 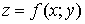 , где
, где 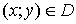 можно понимать (рассматривать) как функцию точки
можно понимать (рассматривать) как функцию точки 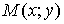 координатной плоскости
координатной плоскости  . В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается
. В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается 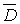 .
.
