Пусть дана квадратная матрица третьего порядка.
ЛИНЕЙНАЯ АЛГЕБРА.
1. Определители 2-го и 3-го порядков, их свойства, вычисление разложением по элементам строки (столбца), по правилу треугольника.
Определителем квадратной матрицы n-го порядка, или определителем n-го порядка, называется число, равное алгебраической сумме n! членов, каждый из которых является произведением n элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как (-1)r(J), где r(J)- число инверсий в перестановке J из номеров столбцов элементов матрицы, если при этом номера строк записаны в порядке возрастания:
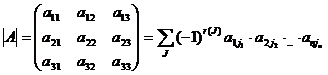 , где сумма берется по всем перестановкам J.
, где сумма берется по всем перестановкам J.
Определителем матрицы второго порядка A=(aij), или определителем второго порядка, называется число, которое вычисляется по формуле:
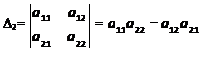
Произведения а11 а22 и а12 а21 называются членами определителя второго порядка. Диагональ, идущая из левого верхнего угла определителя в правый нижний угол называется главной диагональю определителя, а диагональ, идущая из левого нижнего угла в правый верхний угол называется побочной диагональю определителя. Таким образом, чтобы вычислить определитель второго порядка необходимо: из произведения элементов, стоящих по главной диагонали определителя, вычитается произведение элементов, стоящих по побочной диагонали.
Пусть дана квадратная матрица третьего порядка.
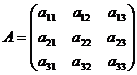
Определителем матрицы третьего порядка A=(aij), или определителем третьего порядка, называется число, которое вычисляется по формуле:
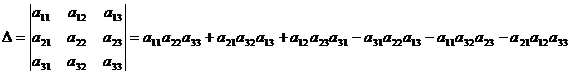 (1.8)
(1.8)
Числа аij (i, j = 1,2,3), образующие определитель называются его элементами, а произведения элементов в правой части (1.8) называют членами определителя. У определителя третьего порядка 9 элементов и 6 членов.
Определитель третьего порядка состоит из 3х строк и 3х столбцов. Первый индекс элемента показывает номер строки, где расположен данный элемент, а второй индекс – номер столбца.
Из (1.8) мы видим, что определитель есть алгебраическая сумма всевозможных произведений его элементов, взятых по одному из каждой строки и каждого столбца, причем знак плюс имеет произведение элементов, стоящих на главной диагонали, и два произведения элементов, образующих в определителе равнобедренные треугольники с основаниями, параллельными главной диагонали, а знак минус имеет произведение элементов, стоящих на побочной диагонали и два произведения элементов, образующих треугольники с основаниями, параллельными побочной диагонали. Схематически это выглядит так:

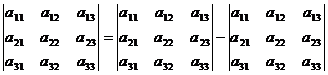
Значение теоремы Лапласа состоит в том, что позволяет свести вычисление определителей n-го порядка к вычислению более простых определителей (n-1)-го порядка.
Свойства определителей.
Определение 5. Квадратная матрица А называется диагональной, если все элементы, не стоящие на главной диагонали, равны нулю.
Операции над матрицами.
1. Умножение матрицы на число. Произведением матрицы A на число 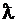 называется матрица B=
называется матрица B= 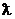 A, элементы которой bij =
A, элементы которой bij = 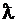 aij для любых i=1,2,…,m; j=1,2,…,n. Общий множитель всех элементов матрицы можно выносить за знак матрицы. В частности, произведение матрицы A на число 0 есть нулевая матрица, т.е. 0*A=0.
aij для любых i=1,2,…,m; j=1,2,…,n. Общий множитель всех элементов матрицы можно выносить за знак матрицы. В частности, произведение матрицы A на число 0 есть нулевая матрица, т.е. 0*A=0.
2. Сложение матриц. Суммой двух матриц A и B одинакового размера m*n называется матрица C=A+B, элементы которой cij=aij+bij для любых i=1,2,…,m; j=1,2,…,n (т.е матрицы складываются поэлементно).
В Частном случае A+0=A.
3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A-B=A+(-1)B.
4. Умножение матриц. Умножение матрицы A на матрицу B определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведение матриц 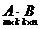 называется такая матрица
называется такая матрица 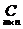 , каждый элемент которой cij равен сумме произведений элементов I-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B:
, каждый элемент которой cij равен сумме произведений элементов I-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B:
cij=ai1b1j+ai2b2j+…+aikbkj= 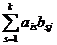 , i=1,2,…,m; j=1,2,…,n.
, i=1,2,…,m; j=1,2,…,n.
Многие операции, присущие операциям над числами, справедливы и для операций над матрицами:
1) A+B=B+A; 5) (A+B)C= AC+BC;
2) (A+B)+C=A(B+C); 6) 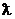 (AB)= (
(AB)= ( 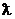 A)B= A(
A)B= A( 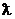 B);
B);
3) 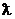 (A+B)=
(A+B)= 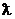 A+
A+ 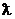 B; 7) A(BC)=(AB)C.
B; 7) A(BC)=(AB)C.
4) A(B+C)= AB+AC;
Необходимо отметить некоторые свойства операции умножения:
1) если произведение матриц AB существует, то после перестановки сомножителей местами произведение матриц BA может и не существовать;
2) если даже произведения AB и BA существуют, то они могут быть матрицами разных размеров;
3) в случае, когда оба произведения AB и BA существуют и оба – матрицы одинакового размера, коммутативный закон умножения, вообще говоря, не выполняется, т.е AB 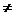 BA.
BA.
5. Возведение в степень. Целой положительной степенью Am(m>1) квадратной матрицы A называется произведение m матриц, равных A, т.е Am=A*A*…A, повторяющихся m- раз. По определению полагают, что A0=E, A1=A. Нетрудно доказать, что AmAk=Am+k, (Am)k=Amk.
6. Транспонирование матрицы. Матрица АТ называется транспонированной по отношению к матрице А, если столбцы матрицы А являются строками матрицы АТ.
Пример: Пусть 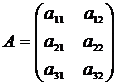 , тогда
, тогда 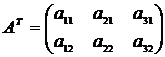
Свойства операции транспонирования:
1) (A/)/=A; 3) (A+B)/=A/+B/;
2) ( 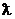 A)/=
A)/= 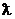 A/; 4) (AB)/=B/A/.
A/; 4) (AB)/=B/A/.
Обратная матрица, основные понятия, алгоритм вычисления.
Обратной для квадратной матрицы A называется такая матрица A-1, что AA-1=A-1A=E.
Решением системы (3.7) называется совокупность значений неизвестных при подстановке которых все уравнения системы обращаются в тождества. Система, имеющая хотя бы одно решение, называется совместной, а система не имеющая ни одного решения, называется несовместной. Система, имеющая единственной решение, называется определенной, система, имеющая более одного решения, - неопределенной.
Рассмотрим матрицу A, составленную из коэффициентов при неизвестных системы (3.7) и матрицу B, получаемую из A добавлением столбца свободных членов:
 и
и 
Матрицу A назовем матрицей системы (3.7), а матрицу B назовем расширенной матрицей системы (3.7). Очевидно, что r (A) £ r (B), так как каждый минор матрицы A будет минором матрицы B, но не наоборот.
I. Метод Крамера.
Метод Крамера рассматривается для систем из n уравнений с n неизвестными, т.е. для систем вида: 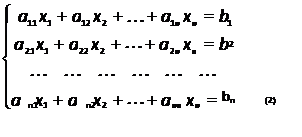
Пусть определитель основной матрицы такой системы отличен от нуля:
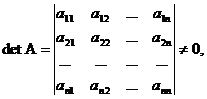
тогда неизвестные x1, x2,…, xn можно найти по формулам Крамера:
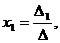
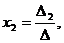 …,
…, 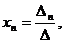
где 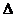 - определитель основной матрицы системы,
- определитель основной матрицы системы, 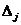 (j=1,n) – определитель, получаемый из
(j=1,n) – определитель, получаемый из 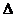 заменой j-го столбца столбцом свободных членов.
заменой j-го столбца столбцом свободных членов.
Если определитель 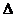 =0, то либо система (2) не имеет решения, либо имеет множество решений. Если все
=0, то либо система (2) не имеет решения, либо имеет множество решений. Если все 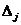 (j=1,n) равны нулю, то система совместна, но неопределенна, если хотя бы одно
(j=1,n) равны нулю, то система совместна, но неопределенна, если хотя бы одно 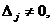 то система (2) не совместна.
то система (2) не совместна.
II. Метод Гаусса.
Вычеркивание уравнения вида
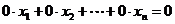
Так как этому уравнению удовлетворяют любые значения неизвестных. Если мы припишем такое уравнение к некоторой системе или, наоборот, вычеркнем его из системы, то новая система будет равносильна первоначальной.
Деление комплексных чисел
Умножение комплексных чисел
Если воспользоваться тригонометрической формой 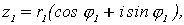
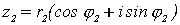 , то произведение
, то произведение 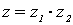 можно записать в виде:
можно записать в виде:
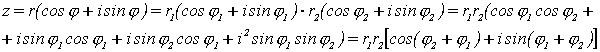 (22.4)
(22.4)
таким образом:
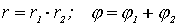 ,
,
Т.е.
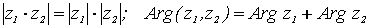 .
.
Эта формула называется формулой Муавра, она показывает, что при возведении комплексного числа в целую положительную степень, модуль возводится в эту степень, а аргумент умножается на показатель степени.
По формуле Эйлера
 (22.8)
(22.8)
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.
5. Векторы, основные определения, понятия, действия над ними.
Вектором называется направленный отрезок с начальной точкой A и конечной точкой B ( который можно перемещать параллельно самому себе). Обозначается 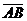 или просто
или просто 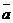 .
.
Длиной ( или модулем) 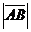 вектора
вектора 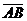 называется число, равное длине отрезка, изображающего вектор.
называется число, равное длине отрезка, изображающего вектор.
Вектор называется нулевым, если его начало и конец совпадают и обозначают 
Уравнение прямой в отрезках
Пусть дана прямая линия, которая не проходит через начало координат и отсекает от координатных осей соответственно отрезки a и b, где a=вел.ОМ, b=вел.ОN.
Покажем, что уравнение этой прямой можно записать в виде 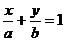 (4.11)
(4.11)
Действительно напишем уравнение прямой в общем виде 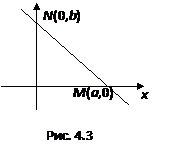
Ax+By+C=0 (4.12)
Т.к. A, B, C одновременно не могут равняться нулю, то однородная система (4.51) должна иметь ненулевое решение. Но однородная система линейных алгебраических уравнений имеет ненулевое решение тогда и только тогда, когда определитель этой системы равен нулю, т.е.
Рисунок 4.11
С другой стороны, по определению скалярного произведения двух векторов имеем:
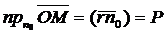 или
или
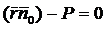 (4.36)
(4.36)
Уравнение (4.36) называется векторным уравнением плоскости. Одновременно уравнение (4.36) называется нормальным уравнением плоскости.
Пусть теперь единичный вектор 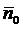 образует с осями координат соответственно углы α, β, γ. Тогда
образует с осями координат соответственно углы α, β, γ. Тогда 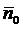 имеет своими координатами направляющие косинусы, т.е.
имеет своими координатами направляющие косинусы, т.е. 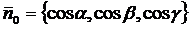 . Далее, вектор
. Далее, вектор 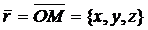 . Тогда получим скалярное произведение векторов:
. Тогда получим скалярное произведение векторов:
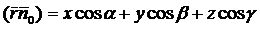
При этом уравнение (4.36) примет вид:
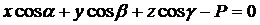 (4.37)
(4.37)
Уравнение (4.36) называется нормальным (нормированным) уравнением плоскости в координатной форме.
Рисунок 4.10
Пусть общее уравнение плоскости имеет вид: Ax + By + Cz + D = 0 (4.31). Подставим в это уравнение координаты точек M, N и R, получим:
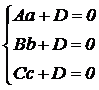 (4.34)
(4.34)
Так как плоскость не проходит через начало координат, то D≠ 0. Так как плоскость отсекает от осей координат ненулевые отрезки, то A≠ 0, B≠ 0, C≠ 0. Тогда из (4.34) имеем: 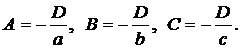
Подставив эти значения в уравнение (4.31), получим: 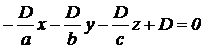 .
.
Так как D≠0, то все члены последнего равенства можно разделить на (-D). Получим:
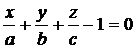 или
или 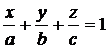 (4.35)
(4.35)
ВВЕДЕНИЕ В АНАЛИЗ.
Или в более точных терминах: введем понятие окрестности точки а: так называется любой открытый промежуток с центром в точке а. Теперь можно сказать, что точка «а» будет точкой сгущения множества x , если в каждой ее окрестности содержатся отличные от а значения x из X.
Действия над пределами.
1. Если 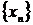 и
и 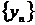 имеют конечные пределы
имеют конечные пределы 
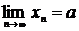
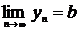 , то и сумма (разность) их также имеет конечный предел,
, то и сумма (разность) их также имеет конечный предел, 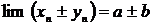
2. Если 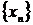 и
и 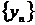 имеют конечные пределы:
имеют конечные пределы: 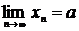
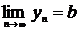 , то их произведение также имеют конечный предел
, то их произведение также имеют конечный предел 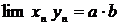
3. Если 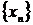 и
и 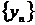 имеют конечные пределы:
имеют конечные пределы: 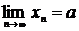
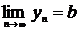 причем b¹0, то их отношение также имеет конечный предел
причем b¹0, то их отношение также имеет конечный предел 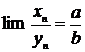 .
.
18. Первый замечательный предел (вывод).
Теорема. 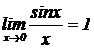 (раскрывает неопределенность типа
(раскрывает неопределенность типа 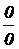 ).
).
Доказательство.
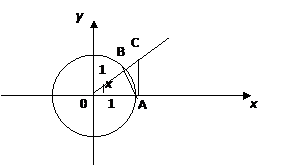
Возьмем круг единичного радиуса и положим  . X – угол выраженный в радианах.
. X – угол выраженный в радианах.
Обозначим площади треугольника ОАВ через– S1, треугольника ОАС – S2, площадь сектора ОАВ – через S.
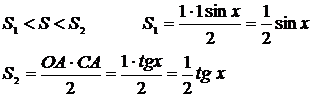
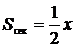
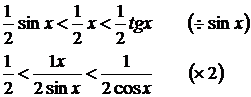
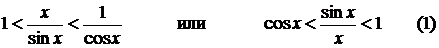
Неравенство (1) получено для 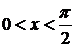 однако cos x и
однако cos x и 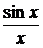 функции четные ,т.к. cos (-x) = cos x.
функции четные ,т.к. cos (-x) = cos x.
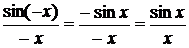 т.е. (1) справедливо и для
т.е. (1) справедливо и для 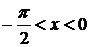 т.к.
т.к. 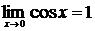 , то из (1) на основании теоремы 5 заключаем
, то из (1) на основании теоремы 5 заключаем 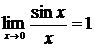 .
.
19. Второй замечательные пределы (вывод). Число e.
Рассмотрим последовательность 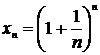 и применим к ней теорему.
и применим к ней теорему.
Устранимый разрыв
Для доказательства достаточно, как и в случае II, перейти к новому, аргументу 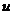 ,
,

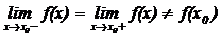 , или f(x0) – не определена. Его можно устранить, если положить значение f(x0) = lim.
, или f(x0) – не определена. Его можно устранить, если положить значение f(x0) = lim.
Разрыв 1-го рода
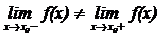 , т.е. не равны левосторонний и правосторонний пределы. Скачок – это разность правостороннего и левостороннего пределов.
, т.е. не равны левосторонний и правосторонний пределы. Скачок – это разность правостороннего и левостороннего пределов.
Разрыв 2-го рода
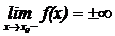 или
или 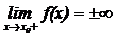
В этом случае прямая x = x0 – вертикальная асимптота функции, т.е. прямая, около которой график уходит в бесконечность.
Правило Лопиталя.
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Итак, если имеется неопределенность вида 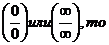
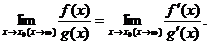 (1)
(1)
Доказательство.
Рассмотрим доказательство теоремы для неопределенности вида 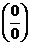 при
при 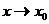 . Предположим, что функции f(x) и g(x), а также их производные непрерывны в точке x0, причем
. Предположим, что функции f(x) и g(x), а также их производные непрерывны в точке x0, причем 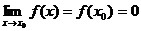 и
и 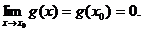
В этом случае 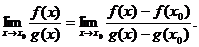
Применяя теорему Лагранжа для функций f(x) и g(x) на отрезке 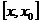 , получим
, получим 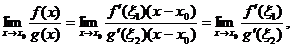 где
где 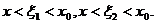
При 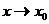 в силу непрерывности производных
в силу непрерывности производных 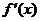 и
и 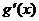 имеем
имеем 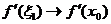 и
и 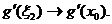
Асимптоты графика.
Определение. Асимптотой графика функции y=f(x) называется прямая линия, к которой неограниченно приближается уходящая в бесконечность ветвь графика. Асимптоты бывают трех типов: «горизонтальные» (параллельные оси Ох), «вертикальные» (параллельные оси Оу) и «наклонные». Первые имеют уравнение у=b, если  , вторые имеют уравнение х=а, если
, вторые имеют уравнение х=а, если 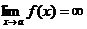 .
.
Пусть прямая y=kx+b является наклонной асимптотой графика функции y=f(x) (см. рис. 5.33).
Из определения асимптоты вытекает, что разность между ординатой точки асимптоты и ординатой точки кривой, соответствующими одной и той же абсциссе, стремится к нулю, когда абсцисса х неограниченно возрастает:
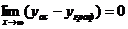 (14.54)
(14.54)
Для отыскания углового коэффициента асимптоты k и ее начальной ординаты b используем условие (14.54), внося в него значения 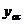 и
и 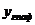 :
:
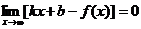 (14.55)
(14.55)
Откуда находим
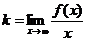 (14.56) (так как
(14.56) (так как 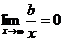 ).
).
Если 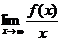 существует и конечен, то, внося найденное значение k в условие (14.55), определяем b:
существует и конечен, то, внося найденное значение k в условие (14.55), определяем b:
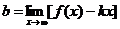 (14.57)
(14.57)
Для существования наклонной асимптоты необходимо существование (и конечность) обоих пределов (14.56) и (14.57). При этом возможны следующие частные случаи.
1. Оба предела существуют, конечны и не зависят от знака х:
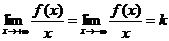 ;
; 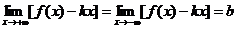
В этом случае прямая y=kx+b будет двухсторонней асимптотой графика (см. ниже пример 1).
2. Оба предела существуют и при 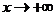 и при но
и при но 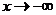
различны между собой:
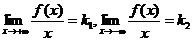 ;
; 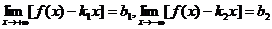 .
.
При этом хотя бы 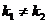 или
или 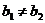 .
.
В этом случае график имеет две односторонние асимптоты: правую
у=k1x-b1 и левую y=k2x+b2 (см. ниже пример 2).
3. Оба предела существуют только при 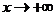 :
:
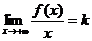 ,
, 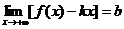 .
.
В этом случае график имеет только правую асимптоту y=kx+b (см. ниже пример 3).
4. Оба предела существуют только при 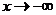 :
:
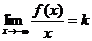 ,
, 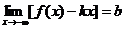 .
.
В этом случае график имеет только левую асимптоту y=kx+b. (Во всех случаях асимптота будет горизонтальной, если k=0.)
Найти экстремумы функции.
Второе достаточное условие экстремума. Теорема. Если первая производная 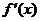 дважды дифференцируемой функции равна нулю в некоторой точке x0, а вторая производная в этой точке
дважды дифференцируемой функции равна нулю в некоторой точке x0, а вторая производная в этой точке 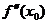 положительна, то x0 есть точка минимума функции
положительна, то x0 есть точка минимума функции 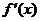 ; если
; если 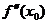 отрицательна, то x0-точка максимума.
отрицательна, то x0-точка максимума.
Схема исследования функции у=f(x) на экстремум:
1. Найти производную 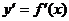 .
.
2. Найти критические точки функции, в которых производная 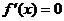 или не существует.
или не существует.
3. Найти вторую производную 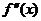 и определить ее знак в каждой критической точке.
и определить ее знак в каждой критической точке.
Найти экстремумы функции.
Третий достаточный признак экстремума. Если в критической точке функции f(x) обращаются в нуль не только первая производная f /(x0), но и все последовательные производные до ( 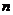 — 1)-й включительно [f'(x0) = =f"(x0) = …=f(n-1)(x0)=0],a производная n-го порядка существует, непрерывна и отлична от нуля
— 1)-й включительно [f'(x0) = =f"(x0) = …=f(n-1)(x0)=0],a производная n-го порядка существует, непрерывна и отлична от нуля 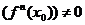 , то точка х0 будет точкой экстремума, если n — число четное, и не будет ею при n нечетном.
, то точка х0 будет точкой экстремума, если n — число четное, и не будет ею при n нечетном.
Характер экстремума при n четном определяется знаком f(n)(x0): максимум при f(n)(x0) <0, минимум при f(n)(x0)>0
35. Функции двух переменных: основные понятия, предел функции двух переменных, непрерывность ыункции двух переменных.
Определение: Пусть задано множество 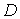 упорядоченных пар чисел
упорядоченных пар чисел 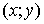 . Соответствие
. Соответствие 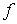 , которое каждой паре чисел
, которое каждой паре чисел 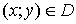 сопоставляет одно и только одно число
сопоставляет одно и только одно число 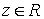 , называется функцией двух переменных, определенной на множестве
, называется функцией двух переменных, определенной на множестве 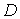 со значениями в
со значениями в  , и записывается в виде
, и записывается в виде 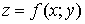 или
или 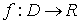 . При этом
. При этом 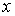 и
и 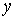 называются независимыми переменными (аргументами), а
называются независимыми переменными (аргументами), а 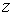 - зависимой переменной (функцией).
- зависимой переменной (функцией).
Множество 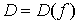 называется областью определения функции. Множество значений, принимаемых
называется областью определения функции. Множество значений, принимаемых 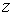 в области определения, называется областью изменения этой функции, обозначается
в области определения, называется областью изменения этой функции, обозначается 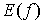 или
или 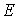 .
.
Определение: Функцию 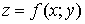 , где
, где 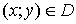 можно понимать (рассматривать) как функцию точки
можно понимать (рассматривать) как функцию точки 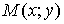 координатной плоскости
координатной плоскости  . В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается
. В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается 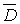 .
.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Таблица основных неопределенных интегралов.
1. 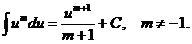 9.
9. 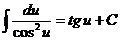
2. 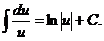 10.
10. 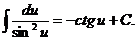
3. 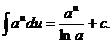 11.
11. 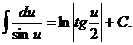
4. 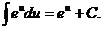 12.
12. 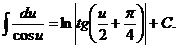
5. 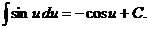 13.
13. 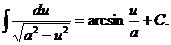
6. 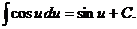 14.
14. 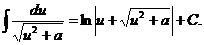
7. 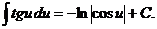 15.
15. 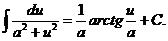
8. 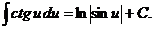 16.
16. 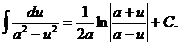
Интегрирование по частям.
Значит
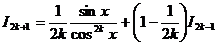
Получена рекуррентная формула. Последовательно применяя эту формулу, получим выражение 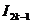 через
через 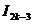 ,
, 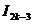 — через
— через 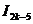 и т. д.; наконец,
и т. д.; наконец, 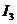 — через
— через 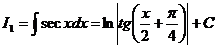 . Используя теперь полученные нами выражения в обратном порядке, найдем
. Используя теперь полученные нами выражения в обратном порядке, найдем 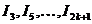 .
.
Далее
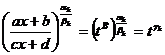 , где
, где 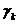 — целое число, поскольку В делится без остатка на каждое из чисел
— целое число, поскольку В делится без остатка на каждое из чисел 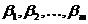 . Имеем
. Имеем 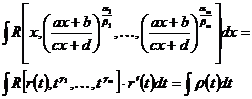
Где 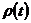 есть рациональная функция аргумента t.
есть рациональная функция аргумента t.
2. Вычисление интегралов от рациональной функции аргумента х и квадратного радикала из квадратного двучлена:
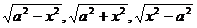 .
.
Вычисление таких интегралов производится с помощью соответствующей тригонометрических подстановок;
1) 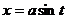 (17.22) в случае интеграла
(17.22) в случае интеграла 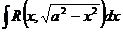 ;
;
2) 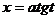 (17.23) в случае интеграла
(17.23) в случае интеграла 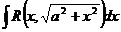
3) 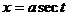 (17.24) в случае интеграла
(17.24) в случае интеграла 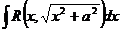 ..
..
Во всех трех случаях подрадикальное выражение превращается в точный квадрат, радикал исчезает, а интеграл получает вид 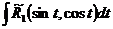 .
.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Формула Ньютона – Лейбница.
Простым и удобным методом вычисления определенного интеграла 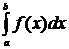 от непрерывной функции является формула Ньютона-Лейбница:
от непрерывной функции является формула Ньютона-Лейбница:
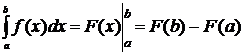 .
.
Применяется этот метод во всех случаях, когда может быть найдена первообразная функции F(x) для подынтегральной функции 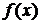 .
.
Интегрирование по частям
Теорема. Если функции 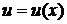 и
и 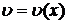 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 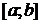 , то имеет место формула
, то имеет место формула
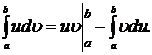 | (5.3.1) |
Приложение определенного интеграла: формулы площадей плоских фигур, длины кривой, объема ткл вращения.
Площади фигур в декартовой системе координат
Площадь фигуры, ограниченной кривыми 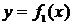 и
и 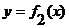 , прямыми х = а и х = b (при
, прямыми х = а и х = b (при 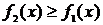 ) можно найти по формуле
) можно найти по формуле 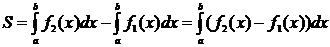 .
.
Длина кривой (дуги).
Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у = f(х), где 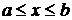 .
.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина ее наибольшего звена стремиться к нулю.
Если функция у=f(х) и ее производная у' = f'(x) непрерывны на отрезке [а;b], то кривая АВ имеет длину, равную
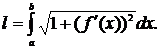 | (4.2.1) |
Классификация событий.
Всякие явления (факты), которые могут произойти или не произойти, называются событиями. Обозначаются: А, В, С… Комплекс условий, при которых событие наступает, называется опытом или испытанием.
События должны обладать так называемой статистической устойчивостью, или устойчивостью относительных частот. Это означает, что в различных сериях испытаний относительная частота (частость) события изменяется незначительно (тем меньше, чем больше число испытаний), колеблясь около постоянного числа.
Число испытаний, в результате которых появляется событие А, должно быть достаточно велико, ибо только в этом случае можно считать вероятность события Р(А) приближенно равной ее относительной частоте.
Рисунок 1.1
Пусть, например, плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу бросается точка. Это означает, что все точки области G «равноправны» в отношении попадания туда брошенной случайной точки. Полагая, что вероятность события А – попадание брошенной точки на фигуру g – пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g, найдем Р(А)= 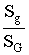 , где Sg и SG – соответственно площади областей g и G (рисунок 1.1). Фигуру g называют благоприятствующей событию А.
, где Sg и SG – соответственно площади областей g и G (рисунок 1.1). Фигуру g называют благоприятствующей событию А.
Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (прямая, отрезок) и трехмерной (некоторое тело в пространстве). Обозначая меру (длину, площадь, объем) области через mes, приходим к следующему определению.
Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области, т.е. P(A)= 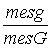 .
.
Следствия.
Формула полной вероятности
Пусть событие А может наступить в результате появления одного из событий Н1, Н2, …,Нn, которые образуют полную группу. Эти события будем называть гипотезами.
Теорема: Полная вероятность события А равна сумме парных произведений всех гипотез, образующих полную группу на соответствующие условные вероятности события А, т.е.
Р(А) = 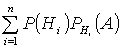
Доказательство:
Р(А) = Р(Н1 А + Н2 А + …+ Нn А) = Р(Н1 А) + Р(Н2 А) + …+ Р(Нn А) = Р(Н1 )РH1 (А) + Р(Н2 )РH2 (А) + Р(Нn )РHn (А).
Формула Байеса
Если событие А в результате испытания произошло, то возможно переоценить вероятность гипотез Нi, образующих полную группу, по формуле Бейеса:
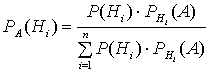 , где Р(Нi) – вероятность гипотезы, РА(Нi) – вероятность гипотезы Нi после переоценки, при условии, что событие А уже произошло; РHi(А) – условная вероятность события А при выполнении гипотезы Нi .
, где Р(Нi) – вероятность гипотезы, РА(Нi) – вероятность гипотезы Нi после переоценки, при условии, что событие А уже произошло; РHi(А) – условная вероятность события А при выполнении гипотезы Нi .
Доказательство.
Для получения искомой формулы запишем теорему умножения вероятностей событий А и Нi в двух формах:
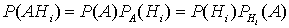 откуда
откуда 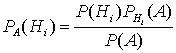 или с учетом формулы полной вероятности
или с учетом формулы полной вероятности 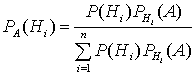 . Эта формула называется формулой Байеса.
. Эта формула называется формулой Байеса.
Формула Бернулли
Пусть производится серия n независимых испытаний, при чем в каждом отдельном испытании вероятность наступления события постоянна – р и отлична от 1 и нуля (т.е. 0 < р < 1), а не вероятность наступления событий - q.
Итак, если в серии n независимых испытаний вероятность наступления события в каждом отдельном испытании постоянна и равна р, то вероятность того, что событие наступит m раз вычисляется по формуле Бернулли (1).
Полученная формула Бернулли на практике используется лишь при n < 10, а при n ® ¥ ее можно заменить другими. Выбор формулы зависит от значений p и q.
Эта характеристика используется как для непрерывной случайной величины, так и для дискретной. Для непрерывной случайной величины график функции распределения – непрерывная кривая, а для дискретной случайной величины – разрывная линия, состоящая из отрезков, параллельных оси ОХ.
Замечание.
Рисунок 6.5
Интегральная функция распределения:
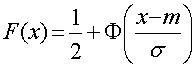 .
.
ЛИНЕЙНАЯ АЛГЕБРА.
1. Определители 2-го и 3-го порядков, их свойства, вычисление разложением по элементам строки (столбца), по правилу треугольника.
Определителем квадратной матрицы n-го порядка, или определителем n-го порядка, называется число, равное алгебраической сумме n! членов, каждый из которых является произведением n элементов матрицы, взятых по
