Определители любого порядка. Свойства определителей.

Сначала опишем основные свойства определителей относительно преобразования матриц. Знание этих свойств поможет упрошать вычисления и находить определители произвольного порядка.

Свойство 1. Определитель не меняется при транспонировании. Это означает, что определитель матрицы равен определителю транспонированной матрицы (матрицы, в которой строки заменены соответствующими столбцами). Исходя из первого свойства, в остальных свойствах мы можем говорить только о строках, подразумевая, что эти свойства применимы также и к столбцам. Свойство 2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.

Свойство 3. От перестановки двух строк определитель меняет свой знак.

Свойство 4. Определитель, содержащий две одинаковые строки, равен нулю.

Свойство 5. Если все элементы некоторой строки умножить на некое число, то сам определитель умножится на это число.

Свойство 6. Определитель, содержащий две пропорциональные строки, равен нулю.

Свойство 7. Если все элементы i-й строки определителя n-го порядка представлен в виде суммы двух слагаемых: a_ij=b_j+c_j, j = 1, ..., n, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, - такие же, как и в заданом определителе, а i-я строка в одном из слагаемых состоит из элементов b_j, в другом - из элементов c_j.

Свойство 8. Если одна из строк определителя есть линейная комбинация его других строк, то определитель равен нулю..

Свойство 9. Определитель не меняется, если к одной из его строк прибавляется любая линейная комбинация других строк.

Теорема (о разложении определителя по строке): определитель равен сумме произведений всех элементов какой-либо строки на их алгебраические дополнения. Это означает, что определитель матрицы n×n равен 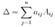(алгебраическое дополнение A_ij=(-1)^i+jM_ij. Здесь минор M_ij - определитель получаемый из основного определителя вычеркиванием i-й строки и j-го столбца)

Теорема о разложении определителя по строке позволяет свести вычисление определителя матрицы n×n к вычислению n определителей матриц (n-1)×(n-1). Таким образом, вычисление определителей с порядком выше третьего сводится к разложению на сумму определителей третьего порядка.

С помощью описанных выше свойств определителей можно провести предварительные преобразования матрицы, облегчающие дальнейшие вычисления. Например, если перед разложением определителя n-го порядка по какой-либо строке накопить в этой строке нули, то разложение приводит к меньшему количеству определителей порядка n-1. Ниже приводится пример, в котором сначала из первой строки вычитается вторая (при этом появляются два нуля), а затем идет разложение по первой строке (из-за двух нулей получается не четыре определителя третьего порядка, а только два): 3.Теорема Лапласа. Миноры и Алгеб.дополнения.Пусть A – квадратная матрица n-го порядка.
Определитель k-го порядка, составленный из элементов матрицы A, расположенных на пересечении строк с номерами i₁ , i₂ , ..., i_k и столбцов с номерами j₁ , j₂ , ..., j_k , называется минором M k-го порядка матрицыA.

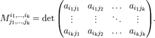
Если из матрицы A вычеркнуть строки и столбцы с такими номерами, то определитель n–k-го порядка полученной матрицы называется дополнительным минором для минора M.

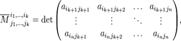
Обозначим символом S сумму индексов, нумерующих строки и столбцы такого минора: S= i₁ + j₁ + i₂ + j₂ + ... + i_k + j_k .

Алгебраическим дополнением минора M называется дополнительный минор для минора M, умноженный на (–1)^S.
Отметим, что алгебраическое дополнение A_{i j} элемента a_{i j} (минора первого порядка) является частным случаем алгебраического дополнения минора.
Теорема Лапласа. Пусть D – определитель n-го порядка, в котором произвольно выбраны k строк (или столбцов), где 1 ≤k ≤ n – 1.
Тогда определитель D равен сумме произведений всех миноров k-го порядка, расположенных в выбранных строках (или столбцах), на их алгебраические дополнения.

4.ОБРАТНАЯ МАТРИЦА.РАНГ МАТРИЦЫ.Понятие обратной матрицы вводится только для квадратных матриц.

Матрица называется обратной матрицей для квадратной матрицы , если 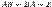. Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A^-1 и удовлетворяющая условию . Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля. Из определения обратной матрицы следует, что матрица 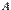является обратной для матрицы 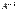, то есть 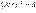. Про матрицы 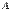и 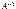можно говорить, что они обратные друг другу или взаимно обратны.

Итак, чтобы найти обратную матрицу нужно:

1.Найти определитель матрицы A.

2.Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу , элементами которой являются числа Aij.

3.Найти матрицу, транспонированную полученной матрице , и умножить её на – это и будет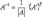

Свойства обратной матрицы

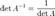· , где det обозначает определитель.

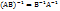· для любых двух обратимых матриц A и B.

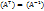· где * 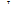обозначает транспонированную матрицу.

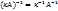· для любого коэффициента .

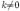Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если 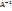существует, то x = 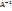b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

Ранг матрицы

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Обычно ранг матрицы A обозначается ( 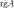) или . 2 метода вычисления ранга матрицы: 1) метод окаймляющих миноров; 2) метод элементарных преобразований. Суть первого метода заключается в следующем. Пусть в матрице A найден ненулевой минор k-го порядка M. Рассмотрим все миноры (k + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется. Что касается второго метода, то воспользуемся элементарными преобразованиями 1) перестановка двух любых строк (или столбцов),2) умножение строки (или столбца) на отличное от нуля число,3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

5. Система n линейных уравнений с n неизвестными. Правило Крамера.Пустьдана система n линейных уравнений с n неизвестными.

или в матричной форме А*Х=В.

Основная матрица А такой системы квадратная. Определитель этой матрицы

называется определителем системы. Если определитель системы

отличен от нуля, то система называется невырожденной.

Найдем решение данной системы уравнений в случае D¹0

Умножив обе части уравнения А*Х=В слева на матрицу A^-1, получим

A^-1*A*X=A^-1*BПоскольку. A^-1*A=E и Е*Х=Х , то

X=A^-1*B (4.1)

Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов

Отыскание решения системы по формуле (4.1) называют матричным способом решения системы.

Матричное равенство (4.1) запишем в виде 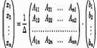то есть Отсюда следует, что Но 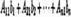есть разложение определителя по элементам первого столбца. Определитель D получается из определителяD путем замены первого столбца коэффициентов столбцом из свободных членов. Итак, 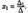Аналогично: 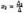, где D 2 получен из D путем замены второго столбца коэффициентов столбцом из свободных членов: ,..., Формулы 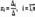называются формулами Крамера.Итак, невырожденная система n линейных уравнений с n неизвестными имеет единственное решение, которое может быть найдено матричным способом, либо по формулам Крамера

Правило Крамера.Если в системе 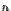линейных уравнений с 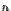неизвестными , то система имеет решение и притом единственное. Это решение задается формулами

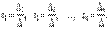
Доказательство. По теореме 14.1 обратная матрица находится по формуле

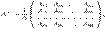
где 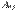-- алгебраические дополнения. Тогда из (15.3) следует, что

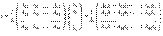Заметим, что по формуле (14.13) разложение определителя 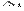по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя 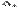по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому 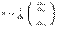, откуда и следует утверждение теоремы.