Геометрическая интерпретация задачи линейного программирования.

Рассмотрим задачу линейного программирования, система ограничений которой задана в виде неравенств

Найти минимальное значение линейной функции

(1.5) Z = С ₁ х ₁ +С ₂ х ₂ +… +С _N x _N

при ограничениях

a ₁₁ x ₁ + a ₂₂ x ₂ + … + a _1N Х _N b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ + … + a _2N Х _N b ₂

(1.6) . . . . . . . . . . .

a _M1 x ₁ + a _M2 x ₂ + … + a _MN Х _N b _M

(1.7) x _j 0 (j = 1, 2, … ,n)

Совокупность чисел х ₁ , х ₂ , …, х _N , удовлетворяющих ограничениям (1.6) и (1.7), называется решением. Если система неравенств (1.6) при условии (1.7) имеет хотя бы одно решение, она называется совместной, в противном случае – несовместной

Рассмотрим на плоскости х ₁ Ох ₂ совместную систему линейных неравенств

a ₁₁ x ₁ + a ₂₂ x ₂ b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ b ₂

. . . .a _M1 x ₁ + a _M2 x ₂ b _M

x ₁ 0, x ₂ 0

Это все равно, что в системе (1.6) – (1.7) положить N=2. Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой

a _i1 x ₁ + a _i2 x ₂ = b _i ,(i = 1, 2, …, m). Условия неотрицательности определяют полуплоскости соответственно с граничными прямыми х = 0, х = 0. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы (рис. 1.1)

Совокупность этих точек (решений) назовем многоугольником решений. Он может быть точкой, отрезком, лучом, много-угольником, неограничен-ной многоугольной облас-тью

Если в системе ограничений (1.6) – (1.7) n = 3, то каждое нера-венство геометрически представляет полупространство трехмерного пространства, граничная плоскость которого a _i1 x ₁ + a _i2 x ₂ + a _i3 x ₃ = b _i ,(i = 1, 2, …, n), а условия неотрицательности – полупрост-ранства с граничными плоскостями соответственно х _j = 0 (j = 1, 2, 3). Если система ограничений совместна, то эти полупространства, как выпуклые множества, пересекаясь, образуют в трехмерном пространстве общую часть, которая называется многогранником решений . Многогранник решений может быть точкой, отрезком, лучом, многоугольником, многогранником, многогранной неограниченной областью. Пусть в системе ограничений (1.6) – (1.7) n 3; тогда каждое неравенство определяет полупространство n-мерного пространства с граничной гиперплоскостью a _i1 x ₁ + a _i2 x ₂ + a _iN x _N = b _i (i = 1, 2, …, m), а условия неотрицательности – полупространства с граничными гиперплоскостями х _j 0 (j = 1, 2, …, n)

Если система ограничений совместна, то по аналогии с трехмерным пространством она образует общую часть n-мерного пространства, называемую многогранником решений, так как координаты каждой его точки являются решением

Таким образом, геометрически задача линейного программирования представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной функции минимальное значение, причем допустимыми решениями служат все точки многогранника решений

79. Графический метод решения задачи линейного программирования для двух переменных.

Наиболее простым и наглядным методом линейного про­граммирования является графический метод. Он применяется для решения задач ЛП с двумя переменными, заданными в не­канонической форме, и многими переменными в канонической форме при условии, что они содержат не более двух свободных переменных.

С геометрической точки зрения в задаче линейного про­граммирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Для нахождения экстремального значения целевой функ­ции при графическом решении задач ЛП используют вектор L() на плоскости Х₁ОХ₂, который обозначим . Этот вектор показывает направление наискорейшего изменения це­левой функции, он равен

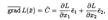
где е₁ и е₂ — единичные векторы по осям OX₁ и ОX₂ соответ­ственно; таким образом, = (∂L/∂х₁, ∂L/∂х₂). Координатами вектора являются коэффициенты целевой функции L().

Алгоритм решения задач

1. Находим область допустимых решений системы ограни­чений задачи.

2. Строим вектор .

3. Проводим линию уровня L₀, которая перпендикулярна .

4. Линию уровня перемещаем по направлению вектора для задач на максимум и в направлении, противоположном , для задач на минимум.

Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допусти­мых решений. Эта точка, определяющая единственное решение задачи ЛП, и будет точкой экстремума.

Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача ЛП будет иметь бесчисленное множество решений. Говорят, что такая задача ЛП имеет альтернативный оптимум, и ее решение находится по формуле

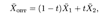
где 0 ≤ t ≤ 1, ₁ и ₂ — оптимальные решения в угловых точках ОДР.

Задача ЛП может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми.

5. Находим координаты точки экстремума и значение це­левой функции в ней.

80. Решение задачи линейного программирования симплекс-методом. Симплексные таблицы. Алгоритм симплекс-метода.

Метод является универсальным, так как позволяет решить практически любую задачу линейного программирования, за­писанную в каноническом виде.

Идея симплексного метода (метода последовательного улуч­шения плана) заключается в том, что начиная с некоторого исходного опорного решения осуществляется последовательно направленное перемещение по опорным решениям задачи к оп­тимальному. Значение целевой функции при этом перемеще­нии для задач на максимум не убывает. Так как число опорных решений конечно, то через конечное число шагов получим оп­тимальное опорное решение. Опорным решением называется базисное неотрицательное решение.