Канонические уравнения прямой

Пусть М₁(x₁, y₁, z₁) – точка, лежащая на прямой l, и 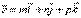– её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

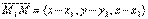Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

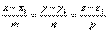– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t. Действительно, из параметрических уравнений получаем 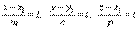или .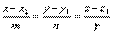

75. Общая постановка задачи оптимизации.

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ^* , который доставляет минимальное значение f(χ^*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

1. Допустимое множество — множество ;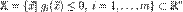

2. Целевую функцию — отображение ;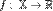

3. Критерий поиска (max или min).

Тогда решить задачу 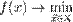означает одно из:

1. Показать, что .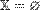

2. Показать, что целевая функция 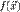не ограничена снизу.

3. Найти .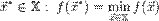

4. Если 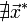, то найти .

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек x₀ таких, что всюду в некоторой их окрестности 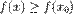для минимума и 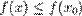для максимума.

Если допустимое множество 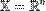, то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

76. Классическая задача на условный экстремум. Необходимое и достаточные условия условного экстремума.

Функция z=f(x,y) имеет в точке Р₀ (x₀,y₀) максимум, если существует такая окрестность точки Р₀, что для всех точек Р (x,y) этой окрестности, отличных от точки Р₀, выполняется неравенство f(x₀,y₀)>f(x,y).

Соответственно, функция z=f(x,y) имеет в точке Р₀ (x₀,y₀) минимум, если существует такая окрестность точки Р₀, что для всех точек Р (x,y) этой окрестности, отличных от точки Р₀, выполняется неравенство f(x₀,y₀)<f(x,y).

Необходимый признак существования экстремума:

Для нахождения экстремумов функции z =f (x,y) сначала нужно найти стационарные точки этой функции, в которых частные производные функции z =f (x,y) равны нулю. Для этого нужно решить систему уравнений:

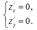(1)

Функция может иметь экстремум также в тех точках, где хотя бы одна из частных производных не существует.

Условие (1) является необходимым условием экстремума, но оно не является достаточным, т.е. в стационарной точке экстремума может и не быть.

Рассмотрим достаточное условие экстремума. Пусть точка M₀ – стационарная точка функции z=f (x,y), которая имеет непрерывные частные производные второго порядка на некоторой окрестности точки M0,

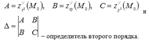
Если D>0, то экстремум в точке M0 есть, при этом M0 – точка минимума при A>0 и M0 – точка максимума при A<0. Если D<0, то экстремума в точке M0 нет.

При D=0 требуются дополнительные исследования функции в окрестности точки M0, мы не будем рассматривать этот случай.

Условный экстремум:

Функция z=f(x,y) имеет в точке Р₀ (x₀,y₀) условный максимум, если существует такая окрестность точки Р₀, что для всех точек Р (x,y) этой окрестности, отличных от точки Р₀, удовлетворяющих уравнению связи φ(x,y)=0, выполняется неравенство f(x₀,y₀)>f(x,y).

Соответственно, функция z=f(x,y) имеет в точке Р₀ (x₀,y₀) условный минимум, если существует такая окрестность точки Р₀, что для всех точек Р (x,y) этой окрестности, отличных от точки Р₀, удовлетворяющих уравнению связи φ(x,y)=0 выполняется неравенство f(x₀,y₀)<f(x,y).

Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Логранжа.

Координаты экстремальной точки должны удовлетворять 3 уравнениям:

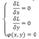
Из этой системы определяются критические точки и соответствующие значения λ.

Достаточным условием экстремума является знакопостоянство d²L(x,y,λ) в критической точке.

77. Метод множителей Лагранжа для решения классической задачи на условный экстремум.

Метод множителей Лагранжа, метод нахождения условного экстремума функции f(x), где 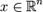, относительно m ограничений 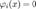, i меняется от единицы до m. Описание метода

· Составим функцию Лагранжа в виде линейной комбинации функции f и функций 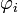, взятыми с коэффициентами, называемыми множителями Лагранжа — λ_i:

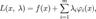
где .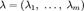

· Составим систему из n + m уравнений, приравняв к нулю частные производные функции Лагранжа 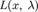по x_j и λ_i.

· Если полученная система имеет решение относительно параметров x'_j и λ'_i, тогда точка x' может быть условным экстремумом, то есть решением исходной задачи. Заметим, что это условие носит необходимый, но не достаточный характер.

Обоснование

Нижеприведенное обоснование метода множителей Лагранжа не является его строгим доказательством. Оно содержит эвристические рассуждения, помогающие понять геометрический смысл метода.

Двумерный случай

Линии уровня 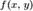и кривая .

Пусть требуется найти экстремум некоторой функции двух переменных 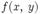при условии, задаваемом уравнением 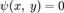. Мы будем считать, что все функции непрерывно дифференцируемы, и данное уравнение задает гладкую кривую S на плоскости 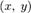. Тогда задача сводится к нахождению экстремума функции f на кривой S. Будем также считать, что S не проходит через точки, в которых градиент f обращается в 0.

Нарисуем на плоскости 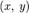линии уровня функции f (то есть кривые 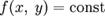). Из геометрических соображений видно, что экстремумом функции f на кривой S могут быть только точки, в которых касательные к S и соответствующей линии уровня совпадают. Действительно, если кривая S пересекает линию уровня f в точке 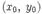трансверсально (то есть под некоторым ненулевым углом), то двигаясь по кривой S из точки 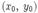мы можем попасть как на линии уровня, соответствующие большему значению f, так и меньшему. Следовательно, такая точка не может быть точкой экстремума.

Тем самым, необходимым условием экстремума в нашем случае будет совпадение касательных. Чтобы записать его в аналитической форме, заметим, что оно эквивалентно параллельности градиентов функций f и ψ в данной точке, поскольку вектор градиента перпендикулярен касательной к линии уровня. Это условие выражается в следующей форме:

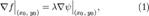
где λ — некоторое число, отличное от нуля, и являющееся множителем Лагранжа.

Рассмотрим теперь функцию Лагранжа , зависящую от и λ:

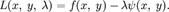
Необходимым условием ее экстремума является равенство нулю градиента 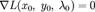. В соответствии с правилами дифференцирования, оно записывается в виде

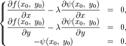
Мы получили систему, первые два уравнения которой эквивалентны необходимому условию локального экстремума (1), а третье — уравнению 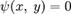. Из нее можно найти 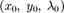. При этом 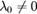, поскольку в противном случае градиент функции f обращается в нуль в точке , что противоречит нашим предположениям. Следует заметить, что найденные таким образом точки 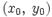могут и не являться искомыми точками условного экстремума — рассмотренное условие носит необходимый, но не достаточный характер. Нахождение условного экстремума с помощью вспомогательной функции L и составляет основу метода множителей Лагранжа, примененного здесь для простейшего случая двух переменных. Оказывается, вышеприведенные рассуждения обобщаются на случай произвольного числа переменных и уравнений, задающих условия.

78. Общая задача линейного программирования. Геометрическая интерпретация задачи.

Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать

Действительно, путь необходимо исследовать на экстремум линейную функцию Z = С ₁ х ₁ +С ₂ х ₂ +… +С _N x _N

при линейных ограничениях

a ₁₁ x ₁ + a ₂₂ x ₂ + … + a _1N Х _N = b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ + … + a _2N Х _N = b ₂

. . . . . . . . . . .

a _М1 x ₁ + a _М2 x ₂ + … + a _МN Х _N = b _М

Так как Z – линейная функция, то = С _j (j = 1, 2, …, n), то все коэффициенты линейной функции не могут быть равны нулю, следовательно, внутри области, образованной системой ограничений, экстремальные точки не существуют. Они могут быть на границе области, но исследовать точки границы невозможно, поскольку частные производные являются константами

Для решения задач линейного программирования потребовалось создание специальных методов. Особенно широкое распространение линейное программирование получило в экономике, так как исследование зависимостей между величинами, встречающимися во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные

1. Общая задача линейного программирования

1. Формулировка задачи.

Даны линейная функция

(1.1) Z = С ₁ х ₁ +С ₂ х ₂ +… +С _N x _N

и система линейных ограничений

a ₁₁ x ₁ + a ₂₂ x ₂ + … + a _1N Х _N = b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ + … + a _2N Х _N = b ₂

. . . . . . . . . . .

a _i1 x ₁ + a _i2 x ₂ + … + a _iN Х _N = b _i (1.2)

. . . . . . . . . . .

a _M1 x ₁ + a _M2 x ₂ + … + a _MN Х _N = b _M

(1.3) x _j 0 (j = 1, 2, … ,n)

где а _ij , Ь _j и С _j - заданные постоянные величины

Найти такие неотрицательные значения х ₁ , х ₂ , …, х _n , которые удовлетворяют системе ограничений (1.2) и доставляют линейной функции (1.1)минимальное значение