Геом интерпр-ия задачи ЛП с несколькими переменными.

Зад.о.наилуч.исп.рес-в

n-прод-и; m-рес-сы; c_j,j=1,n – цена ед-цы прод. j-го вида; b_i,i=1,m – кол-во i-го рес-са; a_ij, j=1,n, i=1,m – кол. i-го рес-са, необход. для пр-ва прод-и j-го вида.Треб-ся опр-ть план пр-ва кажд.прод-и X*=(x₁*,x₂*…x_n*), при кот. обесп-ся max-ая выручка.

Цена общего Vреал-ии:F=c₁x₁+c₂x₂+…+c_nx_n.

Расход на пр-во всех n видов прод-и не должен превышать b_i: a_i1x₁+a_i2x₂+…+a_inx_n≤b_i, i=1,m.

Усл-е неотриц-ти:x_j≥0, j=1,n.

ЭММ:maxF=

x_j≥0

Зад.о.диете

n - кол-вопрод-овпитания;m – питат-евещ-ва; c_j,j=1,n – ценаед-цыпрод-та; b_i,i=1,m – min-екол-во i-гополезноговещ-ва; a_ij, j=1,n,i=1,m –содерж-еi-говещ-вавед-це j-гопрод-та.Треб-сяопр-тькол-воприобретениякажд. видапрод. X*=(x₁*,x₂*…x_n*),обесп-е необх.кол-во полез.вещ-в при min-ой общей стоим-ти прод-в питания.

ЭММ:minF=

x_j≥0

5.Задача о выборе оптимальных технологий. В зада­че о наилуч использ рес-ов опред-ся опти­м-ый план выпуска продукции. Пусть при произ-ве какого-то общественно необход продукта использ-ся nтехнологий. При этом треб-ся т видов рес-ов, задан­ных объемами b_i (i = 1, m). Эффек-ти технологий, т. е. кол-во конечной продукции (в ден. ед.), производ в ед. времени по j-й (j= 1,n) технологии, обозначим c_j. Пусть, далее, а_ij- — расход i-го ресурса в единицу времени по j-й технологии. В качестве неизвестной величины x_jпри­мем интенсивность использ j-й технологии, т. е. вре­мя, в течение которого продукция произв-ся по j-й техно­логии. Пренебрегая временем переналадок, необход для перехода от одной технологии к другой, получаем следующую математическую модель задачи: найти план интенсивностей использования технологий х = (x_i;... ;х_n), обеспеч-ий макс выпуска прод в стоим-ом выраж: ∑a_ijx_j≤b_i (i=1,m) при огранич -ях на лимит-е ресурсы: maxZ= ∑c_jx_j и условии неотрицательности: x_j≥0 (j=1,n).

6.Задача о раскрое материалов.Суть задачи об опти­м-ом раскрое состоит в разраб-ке таких техн-ски допуст планов раскроя, прикот получ-ся необ­ход комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) свод к минимуму. Рассмо­трим простейшую модель раскроя по одному измерению. Бо­лее сложные постановки ведут к задачам целочисл про­грамм-ия. Модель задачи раскроя по одному измер длинномер­ных материалов (прутков, труб, профильного проката и др.) может быть сформул так. Пусть имеется N штук ис­ходного материала, длина каждой штуки равна L. Нужны заготовки т видов, длины которых равны L_i(i = 1,n). Из­вестна потреб-сть в заготовках каждого вида, она равна b{. Изучение вопроса раскроя (построение технол-ой кар­ты раскроя) показ-ет, что можно выделить nприемлемых вариантов раскроя исход матер длиной Lна заго­товки длиной Zj. Обозначим через aijколичество заготовок i-го вида, получаемое при раскрое единицы исходного мате­риала по j-му (j=1,n) варианту, Cj — отходы при раскрое единицы исходн матер по j-му варианту. План задачи х = (х₁;... ; x_j ... ;х_n), где xj— количество единиц исходно­го материала, планируемое к раскрою по j-му варианту.Функция цели — мин отходов, получ при рас­крое: minZ = ∑c_jx_j при огранич: на число ед исх матер: ∑x_j≤N

Формы записи задачи ЛП

Общ.задача ЛП: Max(min)F= ∑Cj*xj

∑ a_ijx_j≤ b_i, i=1,m₁

∑ a_ijx_j= b_i, i=m₁+1,m₂

∑ a_ijx_j≥ b_i, i=m₂+1,m, x_j≥ 0, j=1,m, x_j – произвольн., j= n₂+1,n

Симметр.ф.:

MaxF= ∑Cj*xj

∑ a_ijx_j≤ b_i, i=1,m_, x_j≥ 0, j=1,n или

MinF= ∑Cj*xj

∑ a_ijx_j≥ b_i, i=1,m, x_j≥ 0, j=1,n

Канонич.ф.:

Max(min)F= ∑Cj*xj

∑ a_ijx_j= b_i, i=1,m_, x_j≥ 0, j=1,n

Рассм. 2 вида записи- матричн.и векторн. Введём обознач.Задачу записать матрично:

Max(min)F= C*X; A*X=B; X≥0

Векторн:

Max(min)F= C*X

А₁X₁₊ А₂X_2+…+А_nX_n=B; X≥0

Задачу миним-ции можно заменить максим-цией и наоборот:

Min f(x₁^*, x2^*… xn^*)= - max (-f(x₁^*, x2^*… xn^*))

10.Переход к канон.ф.:

Рассм.задачу:

Max(min)F= ∑Cj*xj (1)

∑ a_ijx_j≤ b_i, i=1,m_{1 (2)}

∑ a_ijx_j≥ b_i, i=m₁+1,m (3)

x_j≥ 0, j=1,n (4)

Преобраз.к канонич.виду.Введём m дополнит.неотриц.перемен: x_n+i≥ 0, i=1,m. Чтобы нер-во (2) преобраз. в р-во,к лев.ч. прибавим дополнит.переменные x_n+i≥ 0, i=1,m1. Чтобы нер-во (3) преобраз.в р-во- вычтем доп.перемен. x_n+i≥ 0, i=m₁+1,m. Нер-ва примут вид:

∑ a_ijx_j+ x_n+i = b_{i ,} i=1,m₁ (5)

∑ a_ijx_j- x_n+i = b_{i ,} i=m₁+1,m (6)

Сист-у ур-ий (5)-(6) наз. Эквивалентной сист-е (2)-(3) с усл. Неотриц-сти дополнит.перем-ых. Они в Цф вводятся с коэф-тами= 0. В рез-те получим задачу в канонич.форме:

Max(min)F= ∑Cj*xj + ∑0*x_n+I(7)

∑ a_ijx_j+ x_n+i = b_{i ,} i=1,m₁ (8)

∑ a_ijx_j- x_n+i = b_{i ,} i=m₁+1,m (9)

x_j≥ 0, j=1,n , x_n+1≥ 0, i=1,m (10)

Теорема:Каждому допустим. реш-ию(x₁⁰, x₂⁰… x_n⁰) задачи (1)-(4) соотв. Вполне определ. допуст-ое реш-е (x₁⁰, x₂⁰… x_n⁰, x_n+1⁰… x_n+m⁰) задачи (7)-(10) и наоборот,где , x_n+i⁰ ≥0, i=1,m.

Т.к. дополнит.перем-е ввод-ся в ЦФ (7) с коэф-ами=0,то знач-я ЦФ (1)и (7) при соотв.допуст.реш-ях одинаковы.Следует, что данные ЦФ на мн-ве соотв.допуст.реш-й достиг. Экстрем.значи-я одновременно. Оптим.реш-ю (1)-(4) соотв. реш-е (7)-(10),т.е. исх.задачи и её канонич.ф. эквивалентны.

11. Переход к сим-ной форме записи задачи, осущ-ся 2-мя спос-ми:

1сп. пусть к задаче ЛП имеются уравн-я рав-ва . Каждое такое огранич-е рав-ва эквив-но в сис-ме нер-в: , . Нер-во вида «≥»*(-1) преобр-ся к нер-вам «≤» и наоборот. 2сп. Рассм-м задачу в канон-м виде: max(min) F= , , i=1,m, x_j≥0, j=1,n преобр-м её к симметр-му виду сис-му огран-й , нап-р, методом Гаусса, можно привести к виду , i=1,m пусть ранг =m, m<n, тогда сис-ма имеет бескон-ное множ-во реш-й. Перем-ные x₁,x_2,…,x_m наз-ся БП, а перем-ные x_m+1,x_m+2…x_n –СП, выразим ЦФ через СП, для этого подставим БП в ЦФ max(min) F= . Испол-я данные обознач-я ЦФ можно записать в след-м виде: F= ▲_0- ▲_jx_j. Из сис-мы , i=1,m в силу того, что все x_j≥0, j=1,n можем записать, что ,i=1,m. Т. Обр. получили симметр-ную форму записи , , i=1,m , x_j≥0, j=m+1,n. Отметим, что в любом случае при подстановке БПпп в ЦФ справедлива формула -это испол-ся для контроля выч-ий при реш задачи симп-ным мет-м. Если некот-е переем-е явл-ся отриц, то они замен-ся разностью 2-х полож-х x_k=x_k’-x_k’’, где x_k’≥0, x_k’’≥0.

12)Т-ма о струк-ре корд-т угловой точки.Если с-ма векторов А₁,А₂,…,A_nсодержит m линейно независимых векторов А₁,А₂,…,A_m, то допустимое решение вида X=(x₁,x₂….x_m,0…0) x_j>0 j=1,m 4); Явл-ся крайней точкой многогранника планов решений. Док-во: Т.к. с-ма векторов А₁,А₂,…,A_mявл-ся линейно независимой, то вектор В м.б. выражен через них единст-м образом A₁x₁+ A₂x₂+…+ A_mx_m=B 5); Предположим, что 4 не яв-ся крайней точкой => её можно пред-ть как выпуклую линейную комбинацию двух других точек X₁,X₂. X=λ₁X₁+ λ₂X_2, где λ₁>0, λ₁+ λ₂=1 6); Точки X₁ и X₂ имеют вид X₁=(¹x₁,¹x₂…¹x_n), X₂=(²x₁,²x₂…²x_n) 7); Подставим 4) и 7) в 6) Получим, что точки x₁ и x₂ имеют такую же стр-ру как x. Поскольку точки x₁ и x₂ принадлежат ОДР => они должны удовлет-ть векторному равенству 5). (A₁x₁¹+ A₂x₂¹+…+ A_mx_m¹=B) – (A₁x₁²+ A₂x₂²+…+ A_mx_m²=B)=A₁(x₁¹-x₁²)+ A₂(x₂¹-x₂²)+….+ A_m(x_m¹-x_m²)=0. Т.к. векторы А₁,А₂,…,A_mлинейно независимые, то последнее равенство выпол-ся при условии x₁¹= x₂¹,…, x_m¹= x_m². Пришли к противоречию, что точку Х невозможно представит как выпуклую комбинацию двух различных точек =>X- крайняя точка.

Основная теорема ЛП

Если ЗЛП имеет решение, то ЦФ достигает экстрем.знач хотя бы в одной из крайних точек многогр.решений.

Если же ЦФ достигает экстрем.знач более чем в одной крайней точке, явл-ся их выпуклой лин.комбинаций.

Док-во:Пусть Х^*-допуст.реш., для кот.ЦФ достигает своего max знач maxF=f(X^*),тогда

f(X^*) (1)

Если Х^* совп с одной из крайних точек, то перв часть теор док-на.

Предпол, что Х^* не явл.крайней точ, то перв многогр реш. Тогда Х^* можно в виде выпуклой линейной комбин точек Х₁, Х₂,…,Х_к:

В силу лин-ти f(X) имеем

f(X^*)= ₁f(X₁)+ ₂f(X₂)+ …+ f(X_k)

Обозн через М maxзнач ЦФ среди чсех крайних точек, т.е.

M=max(f(X₁), f(X₂),…,f(X_k)).

f(X*) ₁M+ ₂M+…+ _kM=M

Или f(X*) M (2)

Из нер-в 1 и 2 вывод f(X*)= M

Но М-знач ЦФ в одной из крайн точек, поэтому Х^*совп с одн из них.

Допуст, что f(X)достиг макс знач более чем в одн точке

f(X₁)=f(X₂)= …=f(X_р)=M

Х= , i 0,(i= ,

f(X)= 1f(X1)+ 2f(X2)+…+ _pf(X_p)= 1M+ 2M+…+ _pM=M,

т.е лин ф-я F приним макс знач в произв точке Х, явл-ся выпукл лин комбин-ей точек Х1,Х2,…,Хр, в которой ЦФ F принимает макс знач.

14) Построение начальнопорн плана

Пусть з-ча ЛП представлена с мат огранич в канонич виде ∑а_ijх_j =b_i, b_i≥0, i=1;m

Огранич-рав-во имеет предпочтит вид, если при неотриц прав части лев часть содерж перемен-ю с коэф-том=1, а в остальн ограничения эта перемен-я входит с коэф-том=0

Сис-ма огранич имеет предпочтительн вид, если кажд огранич-рав-во имеет предпочтит вид. В этом случае легко найти опорн реш( - это базисное с положит координатами)

Для этого все СП надо принять =0, а БП = свободным членам Пусть сис-ма осн огранич имеет вид: ∑а_ijх_j≤b_i, b_i≥0, i=1;m

С пом-ю добавления клев частям дополн неотриц перемен-х дан сис-му можно привести к канонич виду: ∑а_ijх_j+ х_n+i = b_i, b_i≥0, i=1;m

Дан сис-ма имеет предпочтит вид и следоват-но нач опорн план можно записать в виде:

Х₀=(0, 0, 0, … , 0, b₁, b₂, … , b_m)

15) Признак оптим опорн плана. Симплексн таблицаЛюб з-чу ЛП можно свести к виду:

maxF=∆₀ - ∑∆_jx_j

x_i+∑α_ijx_j = b_i, i=1;m

x_j≥ 0, j=1;m

Для реш з-чи запис в симплексн таблицу

Посл строку наз-ют индексн строкой или строкой ЦФ. ∆₀= С_бβ=F(X₀) – значение ЦФ для нач опорн плана Х₀; ∆_j=С_бA_j-C_j, j=m+1;n–оценки СП

Реш з-чи:1) Если з-ча на max, то план оптимальн, если ∆_j≥0, j=1;n; 2) Если з-ча на min, то план оптимальн, если ∆_j≤0, j=1;n

18.Теор:Если в идек-й строке симплек табл сод-щий опт план имеется хотя бы 1 нулевая оценка соот-я СП,то задача ЛП имеет бескон-е мн-во опт-х планов.

След-е:Если в индекс-й строке симпл-ой табл сод-я опти-й план все оценки СП полож-ны, то найд-й оптим-й план единст-й

19.Теор:Если в индеек-й строке симплек-й табл задачи ЛП на max содер-я отриц оценки,а в соот-ем столбце нет ниодного полож-о эл-та,то ЦФ на мн-ве допуст-х планов задачи неогран-на сверху.

Теор: Если в индеек-й строке симплек-й табл задачи ЛП на min содер-я полож-е оценки,а в соот-ем столбце нет ниодного полож-о эл-та,то ЦФ на мн-ве допуст-х планов задачи неогран-на снизу.

Двойст и прям зад-ча

Рассм задачу ЛП вида:

max F=c1x1+c2x2+…+cnxn

а₁₁ х₁ +а₁₂х₂+…+а_1nх_n≤ b₁

а₂₁х₁+а₂₂х₂+…+а_2nх_n≤ b₂

_……..

a_m1х₁+а_m2х₂+…+а_mnх_n≤ b_m

Xj 0 j=1.n₁

двойс к данной задаче назыв-ся задача

min =b₁y₁+b₂y₂+…+b_my_m

а₁₁y₁+а₂₁y₂+…+а_m1y_m≥ c₁

а₂₁y₁+а₂₂ y₂+…+а_2ny_n≥ c₂

_{……………/}

a_1ny₁+а_2ny₂+…+а_mny_n= c_n/ ;yi 0 ;i=1,m_1; yi-любого знака

Правила постр двойств. задачи: 1)Если в прямой задаче ЦФ на мах, то в двойств. будет на мин. И наоборот. 2)Число перем исход задачи = числу основн огранич двойств. задачи и наоборот. 3)Коэфф. При неизв в ЦФ двойств. задачи явл-ся свободн чл прям задачи и наоборот. 4)Матрица, сост-я из коэфф. при неизв в системе осн огранич прям задачи и аналогичная матрица двойств задачи получ-ся друг из д транспонированием.. 5)Если перем прям задачи , то соот-щее огранич в системе основ огранич двойств. задачи явл-ся нерав-во, а если переменная прям задачи может приним любые знач, то соотв огранич явл-ся уравнением.

Теория двойст. Эк сдерж

Рассм пару симм-ых двойств задач:

Max F = ,(1)

Теорема: для любых допуст планов Х=(х_1,х_2…….х_n) и У=(у₁,у₂,…..у_m) прям и двойств задач справедливо нерав-во F(x) (y) т. е.

(7)

Доказ:учитывая неравенства 2 и 5, получаем:

F(x)= =

Эк. содерж: Для любого допуст плана произв-ва Х и любого допуст-го вектора оценок рес-ов У общсозданная стоим-ть не превосходит сумм оценке рес-сов.

Малая теор.двойств.

Для существ.оптим.плана каждый из пары взаимод-их задач необх-мо и дост-но существ-ие допуст-го плана для каждой из них.

24. Перв теорема двойств и ее эк содерж. Теорема: Если 1 из пары двойст задач имеет оптим реш, то другая имеет оптим решение, причем экстрем знач ЦФ совпад: F (X*)=φ(Y*). Если одна из пары дв-х задач неразреш вследствие неогранич-ти ЦФ на множ. доп-х реш, то система огранич другой задачи противоречива.

Док-во:

махF =c₁x₁+c₂x₂+…+c_nx_n

a₁₁x₁+a₁₂ x₂+…+a_1nx_n ≤ b₁+ x_n+1 a_m1x₁+a_m2x₂+…a_mnx_n≤ b+x_n+m

x_j≥0, j=1,n

minφ= b₁y₁+ b₂y₂+…+ b_my_m

a₁₁y₁+a₂₁ y₂+…+a_m1y_m ≥c_{1 -} y_m+1

a_1ny₁+a_2ny₂+…a_mny_n≥c_m - y_n+m

y_i≥0, i=1,m

Введ дополн-х неотриц-х перем х_n+1 >=0,i=1,m прям задачу сведем к кононич-ой форме записи. Аналог-о введ дополн-х неотриц-х перем y_m+j>=0,j=1,n,двойств задачу также можно свести к конон-му виду. Соответствие м. перем.дв-х задач: x₁ x_{2 …}x_n- y_m+1, y_m+2,…, y_m+n-СП, x_n+1, x_n+2,…,x_n+M - y_1, y_2,…,y_m – БП.Реш двойств задачи нах. в индексной строке посл. симпл. табл, содер. оптим. план прям задачи. Эк содерж: если разреш задача опред-ия оптим-го плана максим-го выпуск прод-ии, то разр-ма и задача опр-ия оценок ресурсов. Причем цена пр-ва прод-ии и сумм-ая оценка сов-т.

25. теор о доп-ей нежесткости и ее эк сод-ие. Теорема: для того, чтобы планы Х*, У* пары двойст-х задач были оптим-ми необх и достат вып-ие след-х усл-ий: х_j*(∑а_ijy_i*- с_j)=0, j=1,n (1),y_i*(∑а_ijx_i*- b_i)=0, i=1,m(2). Док-во: необход-ть махF =∑c_jx_j, ∑а_ijx_i*= b_i, i=1,m, x_j≥0, j=1,n.(3)minφ= ∑b_iy_i∑а_ijy_i* ≥с_j, j=1,n y_i≥0, i=1,m. F (X*)=φ(Y*)т.е∑c_jx_j,*= ∑b_iy_i*(4). Подставим в 4b_iиз 3: ∑c_jx_j,*=(∑а_ijx_i*) y_i*= ∑х_j*∑а_ijy_i*→ ∑х_j*(∑а_ijy_i*- с_j)=0 (5).Т.к х_j*≥0, и ∑а_ijy_i*- с_j ≥0, j=1,n. След-но из рав-ва 5 след-т условие 1,усл2док-ся аналогично. Достат-ть: ∑х_j*(∑а_ijy_i*- с_j)=∑х_j*∑а_ijy_i*-∑c_jx_j,*= ∑y_i*∑а_ijx_i* - ∑c_jx_j,*= ∑b_iy_i*-∑c_jx_j,*→F (X*)=φ(Y*). Эк содерж: Двойствоценки могут служ мерой дефицитности ресурсов (ДР).ДР, т.е ресурс по опт-му плану пр-ва исп-ся полностью имеет полож-ю оценку, а избыт-й имеет нулевую оценку.

26. теорема об оценках.Теорема: двойств-е оценки показ-ют приращение ЦФ, вызванное измен-ем св. члена соотв. ограни. ∂F(X*)/∂b_i=y*, i=1,m. (1). Эк. содерж-е: для этого в выраж-ии (1) дифференциалы заменим приращениями, т.е. ∂b_i≈∆b_i, ∂z(x*)≈∆z(x*). Получим ∆z(x*)=у_i*∆b_i; при ∆b_i=1 имеем ∆z(x*)≈y_i*. Отсюда двойств оценка числ-но равна измен-ю ЦФ при измен-ии соотв-го рес-са на ед-цу. Двойств оценки у_i часто наз-ют скрытыми, теневыми или маргинальными оценками рес-сов.

Теор о потенц. Алг теор

План ТЗ Х* явл. Оптим-м, если ему соотв-т система из m+n чисел Ui и Vj, кот.удовл-т след. Усл-м: 1) Ui+Vj=Cij, X*ij≠0; 2) ∆ij=cij-(Ui+Vj)≥0, X*ij=0 Док-во: ТЗ можно рассматр-ть как двойств. задачу к некот. исх. задачи,реш-ой на max. Каждому i-му огранич-ю ТЗ в исх. задаче соотв-т перемен. Ui,i=1,m, а j-му огранич-ю x_1j+x_2j+…+x_mj=b_j перем. Vj, j=1,n. Тогда задача имеет вид: maxφ= 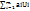+ 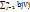, Ui+Vj≤Ciji=1,m, j=1,n Обозн. ч/з X*,Y*(Ui,Vj)-ОП двойств. исх. з-чи. На основ-ии 1-й теор. двойственности равенство: minF=maxφ. А на основании 2-й теор. двойств. выполн. усл.: 1)Ui+Vj=Cij, xij>0; 2)Ui+Vj≤Cij, xij=0, i=1,mj=1,n Из теор. след., что для ОП ТЗ необх. выполн-е усл-й: 1)кажд. занятой кл-ке в распред. табл. соотв. ∑ потенциалов, ровная тарифу этой клетки; 2)кажд. своб. кл-ке соотв-т ∑ потенц-в, не превыш-я тарифа этой кл-ке. Эк-ки оценка показ-т на сколько ден.ед. уменьш. трансп. издержки от загрузки данной кл-ки ед. груза. Алгоритм реш. ТЗ мет. потенциалов.1)Усл.ТЗ записать в форме распред-й табл., но снач. провер. закр. или откр. модель ТЗ. 2) по 1-му из правил строим ОП. 3)Опред-м пот-лы поставщ-в и потреб-й, для этого реш-ся сист. ур-ний Ui+Vj=Cij для занятых кл-к. 4) Опред-ем оценки своб. кл-к ∆ij>0, то получим ОП единствен-й, если хотя бы 1 из оценок ∆ij=0, то имеем бесчислен.мн-во оптим. пл-в.

Циклы и их использ

Для перехода от одного ОП к другому использ-я циклы. Циклпредст. замкн-ю ломаную линию, сост-ю из звеньем, кот пересек-ся под прямым углом. Цикл.включ. 1 своб. кл-ку. В цикле всегда четное число кл-к. Цикл строится для свободн. кл-ки. Если ломанная линия пересек-ся, то точки самопересечения не явл. вершинами. Для наиб перспективн. кл-ки строится замкнутый цикл с вершинами в загружен.кл-х. Вершинами этого цикла усл. приписыв. знаки: своб. кл-ке «+», следующ. «-» и т.д. из поставок в кл-х цикла с «отриц.» верш. выбир. наименьш. кол-во груза, кот перемещ-ся. по кл-м этого цикла: прибавл. в положит. верш. и вычет. в отрицат., в рез-те чего баланс цикла не наруш.

32.Услож постановки ТЗ1)Для мин-ции сумм.затрат на пр-во и перевозку прод-ии, критерий оптим-ти – сумма затрат на пр-во 1ед.груза и на перевозку.2)Если нужно вводить огранич-я, согл. кот-ым отд.поставки от определ.пост-ка опред.потреб-лю должны быть исключены, то в матрице перевозок,содерж-ей оптим.план, определ.клетки должны быть своб-ми(т.е искусств-но завыш.тариф в клетках, перевозки ч/з кот-ые след.запретить)3)нужно учит-ть огран-я по пропуск.спос-ти маршруток. Напр.,если по маршруту A_kB_sможно провести не >d ед.прод-ии, то столбец B_s разбив-ся на 2: Bs’ и Bs’’. В 1-м столбце спрос=разности м/у действит.спросом и огр-ем Bs-d, а во2-м ст-це спрос=d.Тарифы в 2-х ст-ах одинак-ы, а в клетке A_kB_s’тариф иск-но завыш-ся.4)Если некот.поставки по некот.маршр-м должны войти в оптим.план, даже если это невыгодно, то тариф иск-но заниж-ся.

ТЗ с макс-ей ЦФ

1.Нач.опор.план строится методом max тарифа

2.план перевозок – оптим-ый, кот-ым соотв-ет своб.клетки с оценками <=0

3.выбор перспект-ой клетки, кот-ый подлежит заполн-ю, должен произв-ся по полож.оценке

Реш зад ЦП мет отсеч

Будем рассматривать следующую задачу ЦП

Max(min) F=∑ⁿ_j=1c_ijx_ij(1)

∑ⁿ_j=1c_ijx_ij =b_i ,i=1,m (2)

x_j≥0, j=1,n (3)

x_j-целый, j=1,n (4)

Осн в алгоритме- построение доп.огран,кот.наз-ся правильн отсеч.ПО должно удовл.усл:

1)быть линейным

2)отсекать найденное оптим-оенецелочисл-ое решение задачи 1-3:

Алгоритм метода:

1.Реш задача (1)-(3),с отброшенным усл-м целочис-ти(4).

2.Если усл.целочисленности вып-ся по всем переменным,то оптимальн.решение з-чи(1)-(4) совпад-т с оптимальн.решением з-чи(1)-(3).Если же это усл.не выпол-ся хотя бы поодной перемен-й ,то переходим к шагу 3.Если з-ча(1)-(3)не разрешима,то и исходная з-ча не имеет реш-я.

3.Строится доп-ое ограничение,кот.отсекает часть ОДР,в кот.содерж-ся оптим-е решение з-чи (1)-(3) и не содер-ся ни одного допуст-го реш-я задачи(1)-(4)

4.Возвращ-ся к з-че с отброш-м условием целочисл-ти,но с расшир-й сис-мой осн-х ограничений.Добавляются огранич-я,построен-е на 3-ем шаге и вновь примен-ся симплексная процедура и т.д.

36. Метод Гомори (метод отсеч-я)Будем рассм следующую задачу ЦП

Max(min) F=∑ⁿ_j=1c_ijx_ij(1)

∑ⁿ_j=1c_ijx_ij =b_i ,i=1,m (2)

x_j≥0, j=1,n (3)

x_j-целый, j=1,n (4)

Алгоритм метода:

1.Решается задача (1)-(3),с отброшенным усл-м целочис-ти(4).

2.Если усл.целочисленности вып-ся по всем переменным,то оптимальн.решение з-чи(1)-(4) совпад-т с оптимальн.решением з-чи(1)-(3).Если же это усл.не выпол-ся хотя бы поодной перемен-й ,то переходим к шагу 3.Если з-ча(1)-(3)не разрешима,то и исходная з-ча не имеет реш-я.

3.Строится доп-ое ограничение,кот.отсекает часть ОДР,в кот.содерж-ся оптим-е решение з-чи (1)-(3) и не содер-ся ни одного допуст-го реш-я задачи(1)-(4)

4.Возвращ-ся к з-че с отброш-м условием целочисл-ти,но с расшир-й сис-мой осн-х ограничений.Добавляются огранич-я,построен-е на 3-ем шаге и вновь примен-ся симплексная процедура и т.д. Отличие выбора разрешающего элемента: Сначала рассм-ся строка,в кот содерж-ся отриц-е число в столбце свободн.членов и рассмат-ем все неотриц-е числа в этой строке. Выбираем люб.отрицат. число, кот и будет определять разрешающ. столбец. Для чисел с один-ми знаками в столбце свободн. членов и разреш столбце наход-ся симплекс-е отношения. Наименьш.симплексн.отнош и опред разреш-щую строку

37.

1.Явл-ся линейным

2.Отсекает найденное оптимальное нецелочисл-е знач-е з-чи (1)-(3)

3.Не отсекает ни одного из целочис-х реш-ий з-чи (1)-(4).

Рассмотрим i₀ –равенство(1):

x_i0= b_i0-∑x_j?спλ_i0jx_j(2)

a=[a]_{цел.часть}+{a}_{дроб.ч-ть},где 0<{a}< 1

3,7=3+0,7

-4,1=-5 +0,9

Представим b_i0 и λ_i0jв виде суммы дробной и целой части:b_i0=[ b_i0]+{ b_i0}; λ_i0j=[ λ_i0j]+{ λ_i0j}(3)

Подставим (3) в (2), получим:x_i0= ([b_i0]-∑_xj?сп[λ_i0j]xj)+ ([b_i0}-∑_xj?сп{λ_i0j}xj) (4)

Понятно,что 1-ая скобка-в сегда целое число.Для того,чтобы x_i0-было целым числом надо,чтобы величина L_i0={ b_i0}-∑_xj?сп{λ_i0j} xj _,тоже была целым числом.Покажем,что L_i0≤0.Предположим,что L_i0>0.По усл величина ∑_xj?сп{λi0j} xj не может быть отрицат.Т.к.дробные части 0<{λ_i0j}<1.По предложению следует,что дробная часть {b_i0}>1,а это противоречит определению дроб-ой части числа.След-но L_i0≤0Таким образом дополнит-ое огранич,кот.строит в пункте 3 алгоритма должно иметь вид: ([b_i0]-∑_xj?сп{λ_i0j}xj≤0 (5).

38.Теорема. Рассмотрим i₀ –равенство(1):

x_i0= b_i0-∑_xj?спλ_i0jx_j(2);

b_i0=[b_i0]+{ b_i0}

λ_i0j=[ λ_i0j]+{ λ_i0j} (3);

x_i0= ([b_i0]-∑_xj?сп[λ_i0j]xj)+ ([b_i0]-∑_xj?сп{λ_i0j}xj) (4);

([b_i0]-∑_xj?сп{λ_i0j}xj≤0 (5);

Суть теоремы: Нер-во (5)опред-т правильное отсечение Гомори,т.е.:

Max(min) F=∑ⁿ_j=1c_ijx_ij(1)

∑ⁿ_j=1c_ijx_ij =b_i ,i=1,m (2)

x_j≥0, j=1,n (3)

x_j-целый, j=1,n (4)

Метод ветвей и границ.

Для определённости будем рассчит з-чу нахожд макс ф-ции. Суть м-да заключ-ся в том,что сначала реш-ся з-ча без учёта целочис-сти.Если в полученном решении нек.переменные имеют дробные знач,то выбираем любую из дроб-х переменных и по ней строим 2-а ограничения.В первом ограничении величина переменной меньше или равна наименьшему целому числу,а во второй переменной ≥ целому числу +1.Таким образом исходная задача ветвится на 2 з-чи.Решаем каждую из подзадач и находим оптимальное решение.Если получ-е решения опять являются нецелыми,то дальнейшему ветвлению подлежит та ветвь,у которой значение ЦФ будет больше.Процесс решения сопровождается построением деревоветвл-ем.

Понят о ДП.Особен.

ДП(динамическое планирование)-метод нахожд-я реш-я в з-чах с многошаговой стр-рой.Суть метода ДП - идея постепенной, пошаговой оптимизации. Если трудно решить слож-ю задачу,то её след-т разбить на ряд более простых.Каждая новая задача оптим-ся не отдельно от осталь-х,а упр-ние на каждом шаге выбир-ся с учетом всех его последствий.Исключ-е-послед-й шаг,кот. мож. план-ся без учета посдед-вий.Особ-сть ДП:всю ДП целесообр-но разворач-ть от конца к началу

Задача замены оборуд

Т – продолж-ть план. Периода, t – возраст оборуд-ия, r(t) – cтоим. Прод-ции, u(t) – экспл-е затр-ы, s(t) – остат-я стоим., F_k(t) – макс. Прибыль заkлет.

возможнсти: 1)Сохр-ть оборуд-е: тогда прибыль = r(t) – u(t). 2) Продать оборуд.: прибыль = s(t) – p + r(0) – u(0)

Если s(t) – p + r(0) – u(0) >r(t) – u(t), то замена

Если s(t) – p + r(0) – u(0) <= r(t) – u(t), то cохраняем

Общее функцион-е ур-ие:

r(t) – u(t) + F_k-1(t+1), сохран-е

F_k(t) = maxs(t) – p + r(0) – u(0) + F_k-1(1), замена

48.Геометр.интерп-ция з-чиНП.Общ.з-чей НП наз-ся з-ча вида

max(min)F=f (x_1, x_2,…, x_n) (1)

φ_i(x_1,x_2,…,x_n) (2),в кот.либо ЦФ 1,либо огр-ния,либо те и др.нелин-е.В рез-те реш-я эт.з-чи буд.найдена т.Х^* такая,что длялюбой др.т-ки Х,коор-ты кот.также удовл-ют огран-ям з-чи и выпол-ся не=во

f(x^*)>f(x)(если з-ча на min,то f(x^*)<f(x)).В отлич.от з-чиЛП ОДР НПне всегда явл.выпуклой.Т.,в кот.достиг-ся экстр-м ф-ции мож.нах-ся как на границеОДР,так и внутри нее.Алгоритм граф.м-да:строимОДРз-чи,если она пуста,то з-ча не имеет реш-я,2)строим гиперпл-ть f(x_1,x_2,…,x_n)=h,3)опред-им гиперпл-ть наив.(наим.)ур-ня или опр-им неразд-ть з-чи из-за неогр-тиЦФ,4)нах-м т-куОДР,в кот.ЦФ достигает экстр-го знач-я и нах-м в ней знач-е ЦФ.Один-ми знаками в столбце свободн.членов и разреш-м столбце наход-ся симплекс-е отношения.Наименьш.симплексн.отношение и определяет разреш-щую строку

Зад.о.наилуч.исп.рес-в

n-прод-и; m-рес-сы; c_j,j=1,n – цена ед-цы прод. j-го вида; b_i,i=1,m – кол-во i-го рес-са; a_ij, j=1,n, i=1,m – кол. i-го рес-са, необход. для пр-ва прод-и j-го вида.Треб-ся опр-ть план пр-ва кажд.прод-и X*=(x₁*,x₂*…x_n*), при кот. обесп-ся max-ая выручка.

Цена общего Vреал-ии:F=c₁x₁+c₂x₂+…+c_nx_n.

Расход на пр-во всех n видов прод-и не должен превышать b_i: a_i1x₁+a_i2x₂+…+a_inx_n≤b_i, i=1,m.

Усл-е неотриц-ти:x_j≥0, j=1,n.

ЭММ:maxF=

x_j≥0

Зад.о.диете

n - кол-вопрод-овпитания;m – питат-евещ-ва; c_j,j=1,n – ценаед-цыпрод-та; b_i,i=1,m – min-екол-во i-гополезноговещ-ва; a_ij, j=1,n,i=1,m –содерж-еi-говещ-вавед-це j-гопрод-та.Треб-сяопр-тькол-воприобретениякажд. видапрод. X*=(x₁*,x₂*…x_n*),обесп-е необх.кол-во полез.вещ-в при min-ой общей стоим-ти прод-в питания.

ЭММ:minF=

x_j≥0

5.Задача о выборе оптимальных технологий. В зада­че о наилуч использ рес-ов опред-ся опти­м-ый план выпуска продукции. Пусть при произ-ве какого-то общественно необход продукта использ-ся nтехнологий. При этом треб-ся т видов рес-ов, задан­ных объемами b_i (i = 1, m). Эффек-ти технологий, т. е. кол-во конечной продукции (в ден. ед.), производ в ед. времени по j-й (j= 1,n) технологии, обозначим c_j. Пусть, далее, а_ij- — расход i-го ресурса в единицу времени по j-й технологии. В качестве неизвестной величины x_jпри­мем интенсивность использ j-й технологии, т. е. вре­мя, в течение которого продукция произв-ся по j-й техно­логии. Пренебрегая временем переналадок, необход для перехода от одной технологии к другой, получаем следующую математическую модель задачи: найти план интенсивностей использования технологий х = (x_i;... ;х_n), обеспеч-ий макс выпуска прод в стоим-ом выраж: ∑a_ijx_j≤b_i (i=1,m) при огранич -ях на лимит-е ресурсы: maxZ= ∑c_jx_j и условии неотрицательности: x_j≥0 (j=1,n).

6.Задача о раскрое материалов.Суть задачи об опти­м-ом раскрое состоит в разраб-ке таких техн-ски допуст планов раскроя, прикот получ-ся необ­ход комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) свод к минимуму. Рассмо­трим простейшую модель раскроя по одному измерению. Бо­лее сложные постановки ведут к задачам целочисл про­грамм-ия. Модель задачи раскроя по одному измер длинномер­ных материалов (прутков, труб, профильного проката и др.) может быть сформул так. Пусть имеется N штук ис­ходного материала, длина каждой штуки равна L. Нужны заготовки т видов, длины которых равны L_i(i = 1,n). Из­вестна потреб-сть в заготовках каждого вида, она равна b{. Изучение вопроса раскроя (построение технол-ой кар­ты раскроя) показ-ет, что можно выделить nприемлемых вариантов раскроя исход матер длиной Lна заго­товки длиной Zj. Обозначим через aijколичество заготовок i-го вида, получаемое при раскрое единицы исходного мате­риала по j-му (j=1,n) варианту, Cj — отходы при раскрое единицы исходн матер по j-му варианту. План задачи х = (х₁;... ; x_j ... ;х_n), где xj— количество единиц исходно­го материала, планируемое к раскрою по j-му варианту.Функция цели — мин отходов, получ при рас­крое: minZ = ∑c_jx_j при огранич: на число ед исх матер: ∑x_j≤N

Геом интерпр-ия задачи ЛП с несколькими переменными.

Перейдем к геометрической интерпретации ЗЛП с несколькими переменными.

max F = , (1)

b_i, (i= ), (2)

x_j 0, (j= ). (3)

Множ-во реш Х = (х₁,х₂,…,х_n), компоненты кот удовл-ют огранич-ю- равенству a_i1x₁ + a_i2x₂ +… + a_inx_in = b_i, (i= ), геом-ски пред-ют собой гиперплоскость n-мерного пространства. Это выпуклое множ-во.

Множ-во реш Х = (х₁,х₂,…,х_n), ком-ты кот удовл-ют нер-ву a_i1x₁ + a_i2x₂ +… + a_inx_in b_i, (i= ),образ полупрос-во n-мерного простр-ва, кот также явл выпуклым множ-вом.

Множ-во реш, удовл-их системе огранич задачи ЛП (2), (3) предст собой пересечение конечного числа полупространств и поэтому явл выпуклым. Теорема:Множ-во реш ЗЛП выпукло (если оно не пусто). Множ-во реш задачи ЛП в практически важных случаях чаще всего предст-ет собой либо выпуклый многогранник, либо выпуклую многогранную область. ЦФ (1) геом-ки можно рассм как семейство паралл гиперплоскостей с₁x₁ + с₂x₂ +… + с_nx_n =F, каждой из кот соот-ет опред знач параметра F. Вектор = (с₁; с₂; …;с_n), перпенд-ый к гиперплоскости F=const, указ направл наискорейшего возраст функции F. С учетом сказ задача (1)-(3) геом-ки свод. к нахождению точки Х^* = (х₁^*,х₂^*,…,х_n^*) многогранника, опред нерав-ми (2), (3), через кот проход гиперплоскость семейства (1), соот-щая наиб значF. Граф методом можно решить ЗЛП с n>2 перем, если в ее канон-ой записи число неизв n и число линейно-независ векторов m связ соотнош-ем n-m