Ая теорема двойств-ти и ее экон. интерпритация.

Для того, чтобы допустимые решения пары двойственных задач были оптимальными, необходимо и достаточно выполнение условия: xj*(∑aijyi*-cj)=0, j от 1 до n, yi*(∑aijxj*-bi)=0, I от 1 до m. Это условия дополняющей нежесткости. Из них следует: если какое-либо ограничение двойств.задачи обращ-ся оптималь.планом в строгое равенство, то соответствующая компонента опт. плана двойственной задачи должно равняться нулю. Если же какая-то компонента опт. плана равна нулю, то соответствующее ограничение двойств.задачи обращается опт.планом в строгое равенство хj*>0 следовательно (i= от 1 до m)Σaijyi*=cj (затраты на пр-во продукции=цене) – Если продукция вошла в опт.план, то если затраты>цены, объем пр-ва=0 Σaijyi* >cj следовательно xj*=0

yi*>0 следовательно (j=от 1 до n) Σaijxj*=bi (рас-ды рес-ов =запас рес-ов).

(j=от 1 до n) Σaijxj* <bi следовательно yi*=0

Смысл теоремы сводится к следующему:

-если стоимост.оценка рес-ов расход-х на пр-во ед.прод-ии=цене, то этот вид прод-ии входит в оптим.план ;

-если затраты превышают цену, то прод-ию производить не следует;

- еслирасход рес-ов=запасу, то стоимост.оценка этого рес-са положительна. Такой рес-с наз-ся дефицитным. Наибелее дефицит.рес-с обладает наибольшей оценкой;

-если рес-с израсходован неполностью, то его стоимост.оценка = 0.

36. Теорема о сущ-ии плана трансп задачи.

Для его сущ-я необх-мо и достат-но выполн-я усл-я 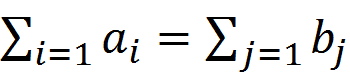. Для любой трансп задачи сущ-ет план.

Теорема о ранге матрицы ТЗ.

Ранг матрицы А трансп.задачи на единицу меньше числа уравнений: r(A)=m+n-1.

39. Алгоритм построения начального опорного плана ЗЛП.

Для нахождения начального опорного плана можно предложить следующий алгоритм:

1. записать задачу в форме жордановой таблицы так, чтобы все элементы столбца свободных членов были неотрицательными, т.е. выполнялось неравенство аio>=0 (i=1,m). Те уравнения с-мы, в которых свободные члены отрицательны, предварительно умножаются на -1.

2.

		-x1 ….. -xn
0=	a1o	a11 …. a1n
…..	…..	………………………..
0=	amo	am1 ….. amn
f=		-c1 …. -cn

Таблицу преобразовывать шагами жордановых исключений, замещая нули в левом столбце соответствующими х. При этом на каждом шаге разрешающим может быть выбран любой столбец, содержащий хотя бы один положительный элемент. Разрешающая строка определяется по наименьшему из отношений свободных членов к соответствующем положительным элементам разрешающего столбца. Если в процессе исключений встретится 0-строка, все элементы которой- нули, а свободный член отличен от нуля, то с-ма ограничительных уравнений решений не имеет. Если же встретится 0-строка, в которой, кроме свободного члена, других положительных элементов нет, то с-ма ограничительных уравнений не имеет неотрицательных решений Если с-ма ограничительных уравнений совместна, то через некоторое число шагов все нули в левом столбце будут замещены х и тем самым получен некоторый базис, а следовательно, и отвечающий ему опорный план.

40. Алгоритм построения оптимального опорного плана ЗЛП.

Начальный опорный план Хо исследуется на оптимальность.

Если в f-строке нет отрицательных элементов (не считая свободного члена), -план оптимален. Если в f- строке нет также и нулевых элементов, то оптимальный план единственный; если же среди элементов есть хотя бы один нулевой, то оптимальных планов бесконечное множество. Если в f-строке есть хотя бы один отрицательный элемент, а в соответствующем ему столбце нет положительных, то целевая функция не ограничена в допустимой области. Задача не разрешима. Если в f- строке есть хотя бы один отрицательный элемент, а в каждом столбце с таким элементом есть хотя бы один положительный, то можно перейти к новому опорному плану, более близкому к оптимальному. Для этого столбец с отриц-ом элементом в f-строке берут за разрешающий; опред-ют по минимальному симплексному отношению разрешающую строку и делают шаг жорданова исключения. Полученный опорный план вновь исследуется на оптимальность. Это повторяется до тех пор, пока не будет найден оптимальный опорный план либо установлена неразрешимость задачи.