Оригинал и изображение по Лапласу

Изображение по Лапласу оригинала в виде постоянной во времени величины

Пусть оригинал является постоянной величиной f(t) = U0 = const. Вычислим интеграл Лапласа:

.

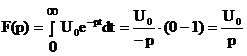Постоянной величине в области изображения соответствует эта же постоянная, делённая на оператор (р).

Не всегда размерность оригинала соответствует размерности изображения.

Существует такое преобразование, аналогичное преобразованию Лапласа, в котором совпадают размерности – это преобразование Карсона:

C(p) = p F(p).

Преобразование Карсона здесь рассматривать не будем.

Изображение показательной функции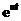

Если функция времени представляет собой показательную функцию 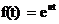, то изображение можно получить с помощью интеграла Лапласа:

.

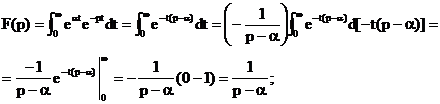
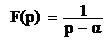Таким образом:

.

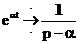Отсюда вытекает ряд важных следствий.

1) Положив a = jw, получим:

.

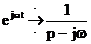2) Функции е-?tt соответствует изображение:

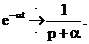
3)

Если функция времени представляет собой синусоидальную величину, например,

ЭДС ,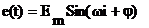

то E(p), при 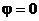, равно:

.

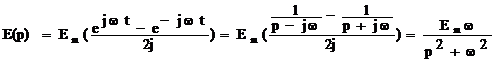Изображение по Лапласу комплексной величины

Пусть 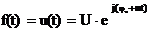, тогда 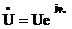при t = 0, и функция времени может быть выражена через комплекс напряжения:

.

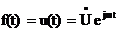Подвергнем вращающийся комплекс преобразованию Лапласа:

.

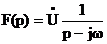Изображение по Лапласу производной функции времени

Известно, что функ­ции f(t) соответствует изображение F(р). Требуется найти изображение первой производной 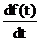, если известно, что значение функции f(t) при t = 0 равно f(0).

Подвергнем функцию 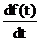преобразованию Лапласа:

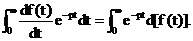
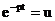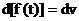Интегрирование произведем по частям. Обозначив и , получим:

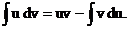
Следовательно,

,

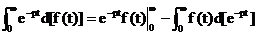но

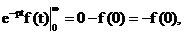a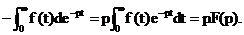

Таким образом,

;

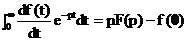Изображение напряжения на индуктивности

Исходить будем из условия, что оригиналу тока i соответствует изображение тока I(р). Запишем оригинал напряжения на индуктив­ности:

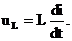
По формуле 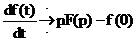определим изображение производной тока:

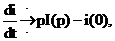
где i(0) – значение тока i при t = 0. следовательно,

.

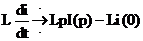Если i(0) = 0, то

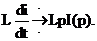
66.Свойства преобразований по Лапласу

Функцией-оригиналом называется комплекснозначная функция f (t) действительного аргумента t, удовлетворяющая условиям:

1. f (t) интегрируема на любом конечном интервале оси t;

2. f (t)=0 для всех отрицательных t;

3. f (t) возрастает не быстрее показательной функции, т. е. существуют такие постоянные М и 0, что |f(t)|<Me0t для всех t.

Изображением функции f (t) (по Лапласу) называется функция F(p) комплексного переменного p= +i , определяемая равенством

.

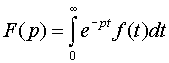Тот факт, что F(p) есть изображение f (t), будем символически записывать так:

.

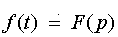Для любой функции-оригинала f (t) изображение определено в полуплоскости Rep>0 и является в этой полуплоскости аналитической функцией.

Из определения изображения следуют его простейшие свойства:

1. Линейность. Для любых комплексных постоянных a и b

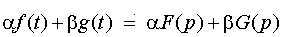
(здесь и далее считать f(t)=F(p), g(t)=G(p)).

2.Теорема подобия. Для любого постоянного a >0

.

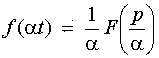3. Дифференцирование оригинала. Если функции f (t), f(t) , f (t),…, f (n)(t) являются функциями-оригиналами и f(t)=F(p), то

,

,

,

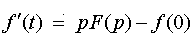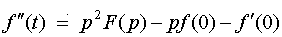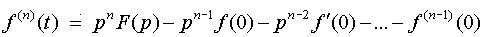где под f (k)(0), (k= 1, 2,…, n-1) понимается .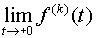

4. Дифференцирование изображения. Дифференцирование изображения сводится к умножению на (-t) оригинала

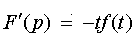
или вообще

.

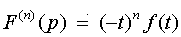5. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р, т. е. если f(t)=F(p), то

.

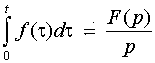6. Интегрирование изображения. Если интеграл 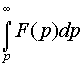сходится, то он служит изображением функции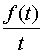

.

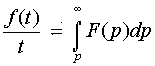7.Теорема смещения. Если f(t)=F(p), то для любого комплексного р0

.

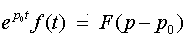8.Теорема запаздывания. Если f(t)=F(p), то для любого t >0

.

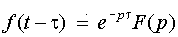Важной для приложений является следующая:

Теорема единственности

Если две функции (t) и (t) имеют одно и то же L-изображение F(p), то эти функции тождественно равны.

Теорема о свертке

Определение. Сверткой функций f1(t) и f2(t) называется функция .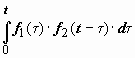
Свёртка обозначается символом f1 * f2: 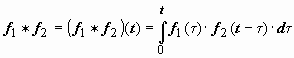. Если f1(t) и f2(t) - функции-оригиналы, то их свёртка - тоже функция-оригинал, показатель роста которой превышает наибольший из показателей роста функций f1(t) и f2(t) не больше, чем на 1. Действительно, пусть 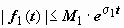, , 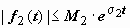, 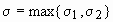тогда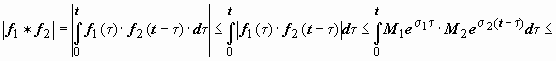 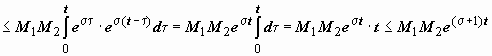, так как t < e t.
Свёртка функций коммутативна: f (t) * g (t) = g (t) * f (t), в этом легко убедиться, заменив в интеграле 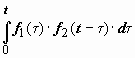переменную τ на τ1 = t −τ.
Можно показать, что свёртка обладает свойством ассоциативности, т.е. что ( f1 * f2 ) * f3 = f1 * ( f2 * f3 ).