Классификация изолированных особых точек однозначной функции

точка а 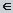Сz называется изолированной особой точкой однозначного характера функции f (z), если f (z) аналитическая и однозначная (регулярная) в кольце {z:0<|z–a|< }, а в самой точке ане определена.

Бесконечно удаленная точка называется изолированной особой точкой однозначного характера функции f (z), если f (z) регулярна в некоторой окрестности {R<|z|< 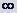} точки z= 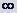и функция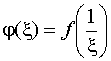

имеет в точке  =0 изолированную особую точку однозначного характера.

В зависимости от поведения функции f (z) вблизи точки а различают следующие три типа особых точек.

Изолированная особая точка а функции f (z) называется

а) устранимой особой точкой, если существует конечный предел

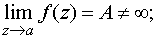
б) полюсом, если

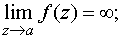
в) существенно особой точкой, если

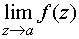
не существует.

Заметим, что типы особых точек z= 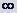функции f (z) и =0 функции совпадают, ибо

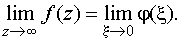
Пусть функция f (z) регулярна в точке а (и, следовательно, в некоторой окрестности этой точки). Число т, т 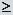1, называется кратностью (или порядком) нуля функции f (z) в точке а, если выполнены условия

f (a)=f (a)=…=f (m-1)(a)=0,

f (m)(a) 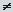0.

При т=1 точка а называется простым нулем функции f (z), при m>1-кратным.

Порядком (или кратностью) полюса функции g(z) в точке а называется кратность нуля в точке а регулярной функции

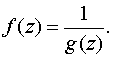
Если а – простой нуль f (z), то точка а называется простым полюсом функции g(z).

Замечание.

Вообще, если

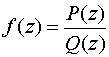, где P(z) и Q(z) – полиномы, не имеющие общих корней, то корни полинома Q(z) (и только они) являются полюсами функции f (z).

Порядок полюса f (z) совпадает с кратностью соответствующих корней полинома Q(z).

Точка z= 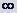называется нулем кратности m 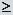1 для функции f (z), регулярной в этой точке, если функция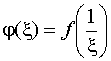

имеет нуль кратности т в точке  =0.

Если z=а – изолированная особая точка однозначного характера для функции f (z), то f (z) регулярна в некотором кольце {z: 0<|z-a|<r} и ее можно разложить в ряд Лорана, сходящийся в этом кольце,

.

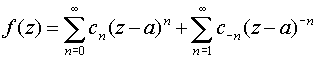Тип изолированной особой точки однозначного характера определяется видом лорановского разложения функции в проколотой окрестности этой точки.

1. Для того чтобы точка а была устранимой особой точкой функции f (z), необходимо и достаточно, чтобы лорановское разложение этой функции в окрестности точки а не содержало главной части.

2. Для того чтобы точка а была полюсом функции f (z), необходимо и достаточно, чтобы главная часть лорановского разложения функции f (z) в окрестности этой точки содержала лишь конечное число членов (причем полюсом порядка т 1, если главная часть имеет вид

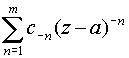, где ст 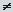0.

3. Точка а тогда и только тогда является существенно особой, когда главная часть лорановского разложения функции f (z) в окрестности этой точки содержит бесконечно много отличных от нуля членов.

Разложение функции f (z) в окрестности бесконечно удаленной точки в ряд Лорана имеет вид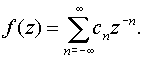

Здесь роль главной части играют члены с положительными степенями z, а члены с отрицательными степенями образуют правильную часть.

Опираясь на приведенные критерии типа особой точки и определение вычета в точке z= 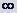, рекомендуем читателю сформулировать соответствующие утверждения для точки z= .

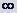60.Вычеты и их приложения

Вычетом функции 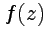в изолированной точке 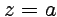называется интеграл

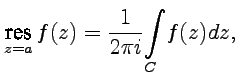(66)

где 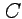- замкнутый контур, содержащий одну особую точку 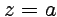. Эквивалентное определение вычета можно получить, сравнивая (66) с выражением для коэффициентов ряда Лорана (61), тогда вычетом функции 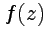называется значение коэффициента 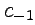ряда Лорана в окрестности точки :

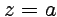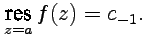(67)

Из определений вычета следует, что если 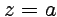- правильная точка функции 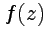, то 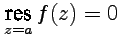. Если точка 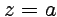является полюсом, то удобно рассмотреть отдельные случаи:

-полюс первого порядка:

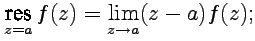(68)

так как в случае полюса первого порядка функция может быть представлена в виде 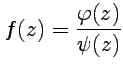, причем 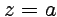- ноль первого порядка функции 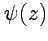, то

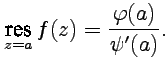(69)

-полюс порядка :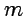

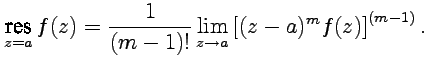(70)

Вычетом функции 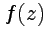в точке 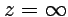называется интеграл

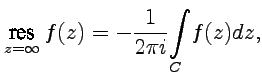(71)

причем во внешней части контура 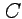функция 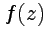не имеет особых точек, находящихся на конечном расстоянии от 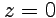. Эквивалентно, с помощью коэффициентов ряда Лорана в окрестности бесконечности, .

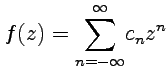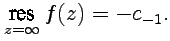(72)

На основе этих определений можно показать, что имеет место следующая теорема:если функция 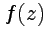является аналитической на полной комплексной плоскости, за исключением конечного числа особых точек (включая бесконечную) 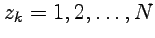, тогда

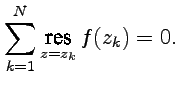(73)

Вычисление вычетов

Вычеты и их применение

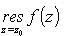- вычет функции f(z) относительно изолированной особой точки z0:

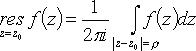
(в круге 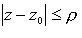нет других особых точек).

Если 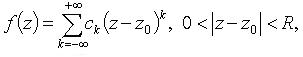то

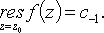
Вычисление вычетов

1. z0 - устранимая особая точка:

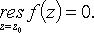
2. z0 - полюс:

а) z0 - простой полюс:

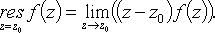
В частности, если 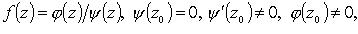то

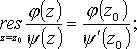
б) z0 - полюс порядка m:

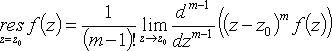
(формула также верна, если z0 - полюс порядка не выше m).

3. z0 - существенно особая точка. Вычет находится по разложению в ряд Лорана.