Ряд фурье по ортогональным системам функций

Последовательность функций 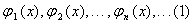непрерывных на отрезке [a,b], называетсяортогональной системой функции на отрезке [a,b], если все функции последовательности попарно ортогональны на этом отрезке, т. е. если

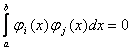
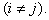
Система называется ортогональной и нормированной (ортонормированной) на отрезке [a,b],

если выполняется условие

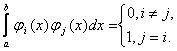
Пусть теперь f(x) - любая функция непрерывная на отрезке [a,b]. Рядом Фурье такой функции f(x) на отрезке [a,b] по ортогональной системеназывается ряд:

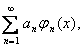
коэффициенты которого определяются равенством:

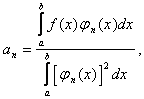n=1,2,...

Если ортогональная система функций на отрезке [a,b] ортонормированная, то в этом случаи

где n=1,2,...

Пусть теперь f(x) - любая функция, непрерывная или имеющая конечное число точек разрыва первого рода на отрезке [a,b]. Рядом Фурье такой функции f(x) на томже отрезке

по ортогональной системе называется ряд:

,

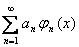Если ряд Фурье функции f(x) по системе (1) сходится к функции f(x) в каждой ее точке непрерывности, принадлежащей отрезку [a,b]. В этом случае говорят что f(x) на отрезке [a,b] разлагается в ряд по ортогональной системе (1).

Интеграл Фурье

Достаточные условия представимости функции в интеграл Фурье.

Для того, чтобы f(x) была представлена интегралом Фурье во всех точках непрерывности и правильных точках разрыва, достаточно:

1) абсолютной интегрируемости на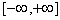

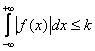(т.е. интеграл сходится)

2) на любом конечном отрезке [-L, L] функция была бы кусочно-гладкой

3) в точках разрыва функции, ее интеграл Фурье определяется полусуммой левого и правого пределов в этих точках, а в точках непрерывности к самой функции f(x)

Интегралом Фурье функции f(x) называется интеграл вида:

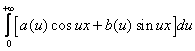
, где ,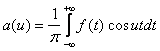

.

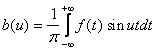Интеграл Фурье для четной и нечетной функции

Пусть f(x)-четная функция, удовлетворяющая условиям представимости интегралом Фурье.

Учитывая, что 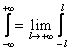, а также свойство интегралов по симметричному относительно точки x=0 интервалу от четных функций, из равенства (2) получаем:

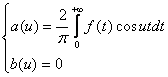(3)

Таким образом, интеграл Фурье четной функции f(x) запишется так:

,

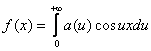где a(u) определяется равенством (3).

Рассуждая аналогично, получим, для нечетной функции f(x) :

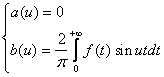(4)

и, следовательно, интеграл Фурье нечетной функции имеет вид:

,

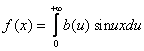где b(u) определяется равенством (4).

Комплексная форма интеграла Фурье

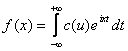, (5)

где

.

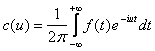Выражение в форме (5) является комплексной формой интеграла Фурье для функции f(x).

Если в формуле (5) заменить c(u) его выражением, то получим:

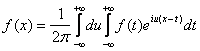, где правая часть формулы называется двойным интегралом

Фуpье в комплексной форме. Переход от интеграла Фурье в комплексной форме к интегралу

в действительной форме и обратно осуществим с помощью формул:

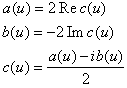
Формулы дискретного преобразования Фурье

Обратное преобразование Фурье.

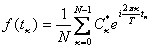
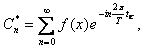
где n=1,2,..., k=1,2,...

Дискретным преобразованием Фурье - называется N-мерный вектор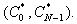

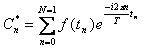
при этом, .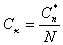

50. Преобразование Фурье

Дискретное преобразование Фурье трансформирует последовательность комплексных (либо вещественных) чисел xn в последовательность комплексных чисел Xn . Прямое и обратное преобразования Фурье определяются, как:

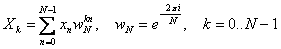
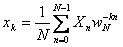
Приведенные выше формулы имеют сложность O(N 2), однако широко известен способ снизить сложность дискретного преобразования Фурье доO(N·log(N)). Быстрое преобразование Фурье широко используется как само по себе, так и для ускорения вычисления других преобразований - быстрого вычисления свертки и кросс-корреляции.