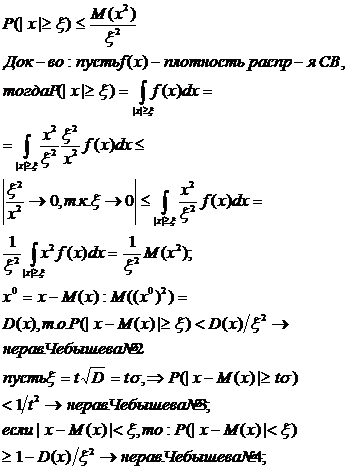Числовые характеристики выборки.

Числовые характеристики выборки дают количественное представление об эмпирических данных и позволяют сравнивать их между собой.

Для выборки можно определить ряд числовых характеристик, аналогичных тем, что в теории вероятности определялись для случайных величин.

Выборочным средним 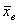называется среднее арифметическое всех значений выборки:
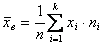1

Выборочное среднее можно записать и так

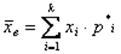2

Отметим, что в случае интервального статистического ряда в равенстве в качестве хi берут середины интервалов, а ni - соответствующие им частоты.
2. Выборочной дисперсией Dв называется среднее арифметическое квадратов отклонений значений выборки от выборочной средней 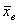, т.е.

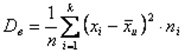3
Или то же самое

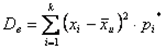4

Можно показать, что дисперсия может быть посчитана по формуле:

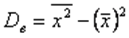5

Здесь

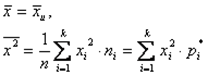
Выборочное среднее квадратическое отклонение выборки определяется формулой

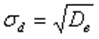7

Особенность выборочного СКО состоит в том, что оно измеряется в тех же единицах. Что и изучаемый признак.
3. При решении практических задач помимо использования формул для расчета выборочной дисперсии используется величина, которая называется исправленной выборочной дисперсией. Дело в том, что значение выборочной дисперсии дает заниженные значения по отношению к действительной дисперсии, поэтому при малых выборках (n < 30) необходимо применять исправленную дисперсию и среднее квадратическое отклонение.
Эти значения находятся по формулам 8-9

В качестве описательных характеристик вариационного ряда используется медиана, мода и размах.

· Размахом вариации называется число R = xmax – xmin, где 10

Xmax - наибольший из вариант,
Xmin - наименьший из вариант.

· Модой М0* вариационного ряда называется вариант, имеющий наибольшую частоту.

· МедианойМе* вариационного ряда называется значение признака, приходящегося на середину ряда.

Если объем выборки n – четное число, то 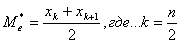11
Если объем выборки нечетное число, то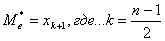

Билет 10

1. Пространство элементарных событий . Алгебра событий. Случайные события.

Событием ТВ наз. Результат опыта, наблюдения, эксперимента…

Случ. событие – событие, которое в результате опыта может произойти, а может и не произойти.

Для каждого опыта мождно указать некоторую совокупность событий. Причем в результате опыта должно осуществиться какое-нибудь из них. Такое множество наз. Пространство элементарн. событий.

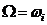, где 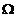- простр. элементарн. событий, 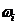- элементарное событие.

События:

1)достоверное(событие, к. в р-те опыта обязательно произойдёт)

2)невозможное(при проведении опыта заведомо не произойдёт)

3)случайное(в р-те опыта м. произойти, а м. и не произойти)

Над событиями проводят следующие действия:

1. 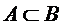(А влечёт за собой событие В, событие В происходит когда происходит событие А)

2. А=В ( , )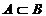

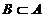3. Суммой А и В наз событие А+В и состоит в том, что произошло или событие А или событие В или оба вместе

4. Произведением А и В называется событие А*В и состоит в том, что событие А и В произойдёт одновременно

5. Противоположными событию А называется событие 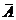и состоитв том что А не произойдёт

Закон больших чисел

Наблюдая массовые однородные случайные явления можно обнаружить в них своеобразные закономерности определенного типа устойчивости (например: при большом числе опытов относительная частота этого события приближается к его вероятности). Этот пример представляет собой частный случай закона больших чисел.

При очень большом числе случайных явлений средний их результат престает быть случайным и может быть предсказан. В узком смысле понимается ряд теорем, в каждой из которых устанавливается факт приближения большого числа опытов к опред. СВ.

Неравенство Чебышева

Для любой СВ х и любого ξ>0 справедливо неравенство Чебышева №1: