Локальная и интегральная теоремы Муавра-Лапласа

Локальная.

Пусть вероятность А в n-независимых испытаний равна р(0<p<1), тогда вероятность P_n(K) определяется по формуле:

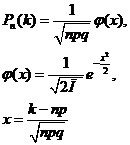
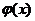-чётная

Интегральная.

Вероятность того что в n-испытаниях событие А, р(0<p<1). Событие наступит не менее к₁раз и не более к₂ раз определяется по формуле:

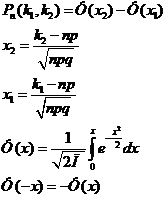
Доверительный интервал для математического ожидания при известном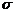

Пусть количественный Х генеральной совокупности признак распределен нормально , причем среднее квадратичное отклонение 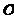этого распределения известно. Требуется оценить неизвестное математическое ожидание 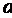повыборочной средней 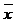. Найдем доверительные интервалы покрывающие параметр 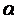с точностью .

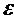Будем рассматривать выборочную среднюю 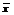как случайную величину 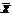и выборочные значения признака x₁,x₂,…,x_n- как одинаково распределенные независимые случайные величины X₁,X₂,…,X_n.

Если случайная величины Х распределена нормальна , то выборочная средняя ,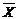

найденная по независимым наблюдениям , также распределена нормально. Параметры распределения 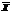таковы

М( )= , ( )= /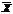

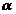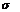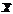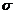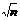
Должно выполняться соотношение

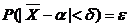
Пользуясь формулой вычисления вероятности заданного отклонения

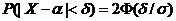
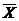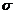заменив Х на и на 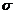( 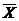)= 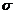/ 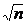получаем

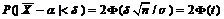
где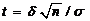

Из последнего равенства получаем 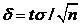можно записать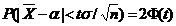

Приняв во внимание ,что вероятность Р задана и ровна 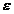, окончательно имеем

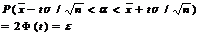
Смысл полученного такой : с точностью 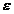можно утверждать , что доверительный интервал 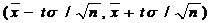покрывает н

Билет 3

Формула полной вероятности

Вероятность события А, которое может наступить при условии появления одного из несовместных событий Н₁,Н₂,…,H_nобразующие полную группу событий равна сумме произведений вероятностей этих событий на соотв. вероятность события А:

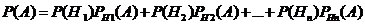
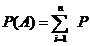
Доказательство: События Н₁,Н₂,…,H_nобразуют полную группу. Их сумма есть достоверное событие: Н₁ +Н₂+…+H_n= 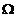по условию А – может произойти с событием H_i, т.е. произойдёт одно из АН₁,АН₂,…,АH_n

А=АН₁+АН₂+…+АН_N, тогда Р(А)=Р(АН₁+АН₂+…+АН_n) =несовместные=Р(АН₁)+Р(АН₂)+…+Р(АН_n)=события зависимые=Р(Н₁)Р_H1(А)+..+P(H_n)P_Hn(A)

Нормальное распределение вероятностей непрерывных СВ.

Опр.: Говорят, что НСВ распределена по норм. Закону с параметрами а,σ, если плотность распределения имеет вид:

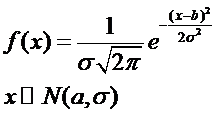
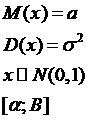
Вероятность попадания СВ в интервал [α,B]: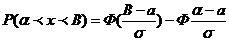

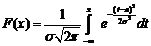- нормальный закон распределения

Полигон и гистограмма

Для наглядности строят различные графики статистического распределения.

По данным дискретного вариационного ряда строят полигон частот или относительных частот.

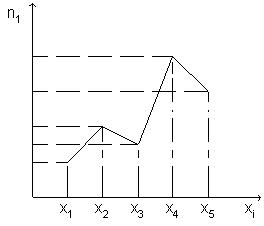
Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2), ..., (xk;nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки ( xi; ni) соединяют отрезками прямых и получают полигон частот (Рис. 1).

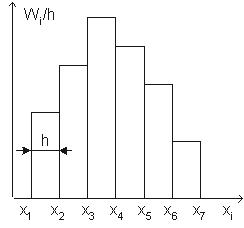
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению Wi / h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии Wi / h (Рис. 2).

Билет 4