Интервальные оценки Доверительный интервал

Интервальное оценивание — один из видов статистического оценивания, предполагающий построение интервала, в котором с некоторой вероятностью находится истинное значение оцениваемого параметра.

Определение:

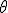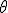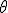Пусть - неизвестный параметр генеральной совокупности. По сделанной выборке по определенным правилам находятся числа 1 и 2 такие чтобы выполнялось неравенство:

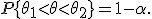
Интервал 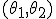является доверительным интервалом для параметра 0, а число 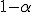- доверительной вероятностью или надежностью сделанной оценки. Обычно надежность задается заранее, причем выбираются числа близкие к 1 (0.95, 0.99 или 0.999).

Доверительный интервал — это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью.

Определение :

Пусть X1..Xn- выборка из некоторого распределения с плотностью 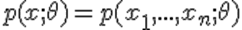, зависящей от параметра 0 , который может изменяться в интервале 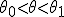. Пусть 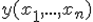- некоторая статистика и 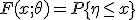- функция распределения случайной величины 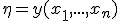, когда выборка 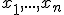имеет распределение с плотностью 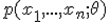. Предположим, что 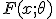есть убывающая функция от параметра 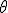. Обозначим 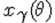квантиль распределения 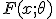, тогда есть возрастающая функция от 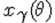. Зафиксируем близкое к нулю положительное число 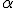(например, 0,05 или 0,01). Пусть 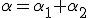. При каждом 0 неравенства 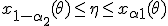(1)

выполняются с вероятностью 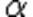-1 , близкой к единице. Перепишем неравенства (1) в другом виде: 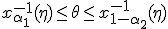(2)

Обозначим 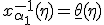, 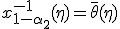и запишем (2) в следующем виде: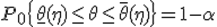

Интервал 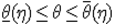называется доверительным интервалом для параметра 0, а вероятность 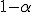- доверительной вероятностью.

Уровень значимости статистического теста — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, falsepositive), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна.

В стандартной методике проверки статистических гипотез уровень значимости фиксируется заранее, до того, как становится известной выборка .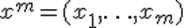

Чрезмерное уменьшение уровня значимости 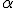может привести к увеличению вероятности ошибки второго рода, то есть вероятности принять нулевую гипотезу, когда на самом деле она не верна. Вероятность ошибки второго рода 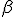связана с мощностью критерия 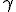простым соотношением 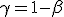. Выбор уровня значимости требует компромисса между значимостью и мощностью или (что то же самое, но другими словами) между вероятностями ошибок первого и второго рода.

Обычно рекомендуется выбирать уровень значимости из априорных соображений. Однако на практике не вполне ясно, какими именно соображениями надо руководствоваться, и выбор часто сводится к назначению одного из популярных вариантов 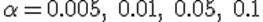. В докомпьютерную эпоху эта стандартизация позволяла сократить объём справочных статистических таблиц. Теперь нет никаких специальных причин для выбора именно этих значений.

Билет №2

Формула Байеса

Если событие A происходит с гипотезами Н₁,Н₂,…,H_nи если событие А уже произошло, то можно опред. Вероятности гипотез после проведения опыта.

Теор: пусть событие А может наступить при появлении одного из несовместных событий Н₁,Н₂,…,H_nкоторое образует группу событий. Если А уже произошло, то вероятность гипотезы H_iможет определиться по формуле Баейса:

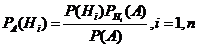
Док: 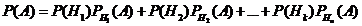будем искать вероятности: 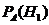, , 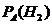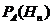например найдём 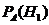по формуле Р(АН₁)=Р(Н₁)Р_Н1(А)=Р(А)Р_А(Н₁)

следовательно найдём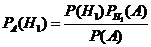

Формула позволяет переоценить вероятности гипотез после того как произошло событие А.