Условная вероятность. Зависимые и независимые события. Теоремы умножения вероятностей

Билет №1

Условная вероятность. Зависимые и независимые события. Теоремы умножения вероятностей

Событие А – независимо от события В, если вероятность А не зависит произошло В или нет. Событие А – зависимо от В, если вероятность А меняется в зависимости произошло В или нет.

Вероятность А вычисленное при условии, что произошло В называется условной вероятностью события А и обозначается: Р(А/В) Рв(А)

Теорема умножения вероятностей независимых событий: Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

P(AB)=P(A) ·P(B);

P(A₁,A_2….A_n)=P(A₁) ·P(A₂) ·..·P(A_n);

Биномиальное распределение вероятностей дискретных СВ

Опр. Говорят,что дискретные случайные величина имеет биномиальное распределное распределение, если возможное значение 0,1,2,…,n

P_k(P(x=k) =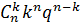

На практике биномиальное распределения показывает, когда пр-сяn-независимых опытов в каждом из которых событие А появляется с вероятностью Р.

Биномиальный закон зависит от двух параметров, найдем биномиальные характеристики от двух параметров.

n=2 p

x 0 1 2

p 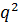2pq p²

M(x)= 0*q²+1*2*p*q+2*p²-2*p

Найдемдисперсию

D(x)=M(x²)-(M(x))²=2p(p+1)-4p²=[M(x²)=0²*q²+1²*2pq+2²*p²]=2p(1-p)=2pq

В случае n=2 M(x)=2p; D(x)=2pq

N=3 x 0 1 2 3

Pq³ 3q²p 3qp²p³

M(x)=3p

D(x)=3pq

Для биномиального закона

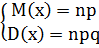
Билет №2

Формула Байеса

Если событие A происходит с гипотезами Н₁,Н₂,…,H_nи если событие А уже произошло, то можно опред. Вероятности гипотез после проведения опыта.

Теор: пусть событие А может наступить при появлении одного из несовместных событий Н₁,Н₂,…,H_nкоторое образует группу событий. Если А уже произошло, то вероятность гипотезы H_iможет определиться по формуле Баейса:

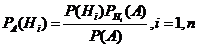
Док: 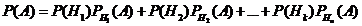будем искать вероятности: 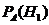, , 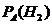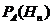например найдём 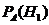по формуле Р(АН₁)=Р(Н₁)Р_Н1(А)=Р(А)Р_А(Н₁)

следовательно найдём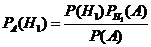

Формула позволяет переоценить вероятности гипотез после того как произошло событие А.

Билет 3

Формула полной вероятности

Вероятность события А, которое может наступить при условии появления одного из несовместных событий Н₁,Н₂,…,H_nобразующие полную группу событий равна сумме произведений вероятностей этих событий на соотв. вероятность события А:

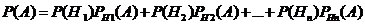
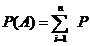
Доказательство: События Н₁,Н₂,…,H_nобразуют полную группу. Их сумма есть достоверное событие: Н₁ +Н₂+…+H_n= 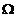по условию А – может произойти с событием H_i, т.е. произойдёт одно из АН₁,АН₂,…,АH_n

А=АН₁+АН₂+…+АН_N, тогда Р(А)=Р(АН₁+АН₂+…+АН_n) =несовместные=Р(АН₁)+Р(АН₂)+…+Р(АН_n)=события зависимые=Р(Н₁)Р_H1(А)+..+P(H_n)P_Hn(A)

Нормальное распределение вероятностей непрерывных СВ.

Опр.: Говорят, что НСВ распределена по норм. Закону с параметрами а,σ, если плотность распределения имеет вид:

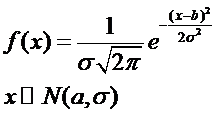
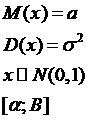
Вероятность попадания СВ в интервал [α,B]: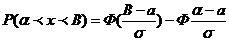

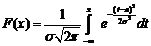- нормальный закон распределения

Полигон и гистограмма

Для наглядности строят различные графики статистического распределения.

По данным дискретного вариационного ряда строят полигон частот или относительных частот.

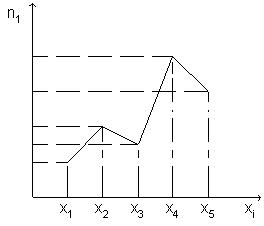
Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2), ..., (xk;nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки ( xi; ni) соединяют отрезками прямых и получают полигон частот (Рис. 1).

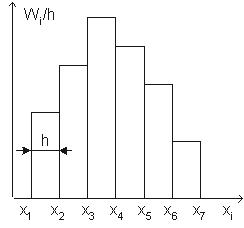
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению Wi / h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии Wi / h (Рис. 2).

Билет 4

Билет 5.

1. Классическое, геометрическое, аксиоматическое и статистическое определение вероятностей.

Вероятность события – математическая оценка возможности появление случайного события в результате опыта.

Если m- число событий благоприятствующих событию A, то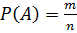

Свойство вероятностей события А:

1.

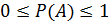
2.

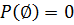
3.

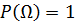
4. А,В – несовместные P(A+B)=P(A)+P(B)

Пусть происходит эксперимент и событие А появляется в М из N, тогда 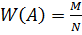– относительная частота события.

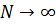- остаётся примерно постоянным.

Статистическое определение вероятности заключается в том что за вероятность события А принимается её относительная частота.

Аксиоматическое определение вероятности: вероятность события А это функция Р(А) удовлетворяющая след. свойствам:

1. P(∅)=0

2. P(Ω)=1

3. 0≤P(A)≤1

4. Ai – несовместное событие i=1,..,n то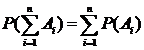

Геометрическое определение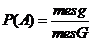

Билет 6

Повторение испытаний

Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.

Если в результате п опытов событие А наступает ровно т раз, то остальные п-т раз это событие не наступает. Событие А может появиться т раз в п испытаниях в различных комбинациях, число которых равно количеству сочетаний из п элементов по т. Это количество сочетаний находится по формуле:

6.1.2. Распределение Пуассона

Говорят,что случайная величина распределена по закону Пуассона,если ее возможное значение 0,1,2,…,л… а соответственные вероятности определяться по формуле P_k=P_n(x=k)= 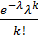, k=0,1,2,…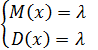

Билет №7

Билет № 9.

Билет 10

1. Пространство элементарных событий . Алгебра событий. Случайные события.

Событием ТВ наз. Результат опыта, наблюдения, эксперимента…

Случ. событие – событие, которое в результате опыта может произойти, а может и не произойти.

Для каждого опыта мождно указать некоторую совокупность событий. Причем в результате опыта должно осуществиться какое-нибудь из них. Такое множество наз. Пространство элементарн. событий.

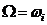, где 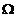- простр. элементарн. событий, 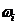- элементарное событие.

События:

1)достоверное(событие, к. в р-те опыта обязательно произойдёт)

2)невозможное(при проведении опыта заведомо не произойдёт)

3)случайное(в р-те опыта м. произойти, а м. и не произойти)

Над событиями проводят следующие действия:

1. 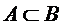(А влечёт за собой событие В, событие В происходит когда происходит событие А)

2. А=В ( , )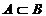

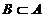3. Суммой А и В наз событие А+В и состоит в том, что произошло или событие А или событие В или оба вместе

4. Произведением А и В называется событие А*В и состоит в том, что событие А и В произойдёт одновременно

5. Противоположными событию А называется событие 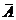и состоитв том что А не произойдёт

Закон больших чисел

Наблюдая массовые однородные случайные явления можно обнаружить в них своеобразные закономерности определенного типа устойчивости (например: при большом числе опытов относительная частота этого события приближается к его вероятности). Этот пример представляет собой частный случай закона больших чисел.

При очень большом числе случайных явлений средний их результат престает быть случайным и может быть предсказан. В узком смысле понимается ряд теорем, в каждой из которых устанавливается факт приближения большого числа опытов к опред. СВ.

Неравенство Чебышева

Для любой СВ х и любого ξ>0 справедливо неравенство Чебышева №1:

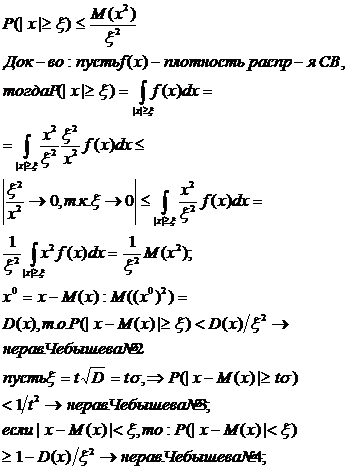
Билет №1

Условная вероятность. Зависимые и независимые события. Теоремы умножения вероятностей

Событие А – независимо от события В, если вероятность А не зависит произошло В или нет. Событие А – зависимо от В, если вероятность А меняется в зависимости произошло В или нет.

Вероятность А вычисленное при условии, что произошло В называется условной вероятностью события А и обозначается: Р(А/В) Рв(А)

Теорема умножения вероятностей независимых событий: Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

P(AB)=P(A) ·P(B);

P(A₁,A_2….A_n)=P(A₁) ·P(A₂) ·..·P(A_n);