Теорема Кронекера - Капелле. Решение произвольных линейных систем.
Теорема Кронекера-Капелли: система линалгур-ий совместна, когда rangA=rang 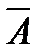 (волнистая). Теорема: если rang совместной системы= числу неизвестных, то система имеет одно решение. Теорема: если ранг совместсист< числа неизвестных, то система имеет бесконеч решений.
(волнистая). Теорема: если rang совместной системы= числу неизвестных, то система имеет одно решение. Теорема: если ранг совместсист< числа неизвестных, то система имеет бесконеч решений.
Правило решения СУ.
1)найти ранг основной и расширенной матрицы (если rA не =rA с крыш, то система несовместна.
2) если rA=rA с крыш и =r, то система совместна и надо найти базисный минор порядка r.
3)Берём rур-ий из коэфкоторых составлен базисн минор. Остальные ур-ия отбрасываем. Неизвестные, коэф которых входят в минор наз главными. Из оставл слева, а остальные (n-r) – справа.
4)Найти выражения главныхнеизв через свободные. Получено общее решение системы
5)Придавая свободным низвестным произвольное значение, получим соотв значения главннеизв, т.е. найдём частные решения.

14. Система однородных линейных уравнений.
АХ=В – система и параллельно рассмотрим систему АХ=0. (АХ=В – Неоднородн. СЛАУ, АХ=0 – однородн. СДАУ).
Одновременно выполняется:
1. АХ=0 имеет тольок тривиальное решение, АХ=В имеет единственное решение или не имеет решений совсем.
2. АХ=0 имеет нетривиальное решение, АХ=В имеет бесконечное число решений.
Рассмотрим подробнее 2-ой случай: r(A) = r(A с волной сверху)<m..
M – r(A) – дефект, количество свободных неизвестных.
Пример: 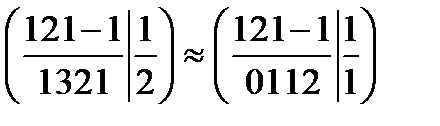 ,
,
б.м: х1, х2
св.м: х3, х4.
х2 + х3 +2х4 = 1., х2 = 1 – а – 2b, х3 = а, х4 = b.
х1 = -2х2 – х3 + х4 + 1 = -2 + 2а +4b – а + b+1 = -1 + а + 5b.
Ответ: (-1 + а + 5b., 1 – а – 2b , а, b)Т.

15. Решение систем линейных уравнений методом последовательного исключения неизвестных (метод Гаусса).
Метод Гаусса для решения системы линейных уравнений
1. Выражаем первое неизвестное из первого уравнения и подставляем его в остальные уравнения.
2. Получаем новую систему, в которой число уравнений и неизвестных на 1 меньше.
3. С новой системой поступаем таким же образом и так продолжаем до тех пор, пока не останется одно линейное уравнение, которое легко решается.
4. Когда получено значение последнего неизвестного xn, подставляем его в уравнение, которое позволяет найти xn – 1 по xn.
5. Понайденным xn – 1 и xn находим xn – 2 и таким образом находим последовательно все неизвестные.

16. Размерность и базис линейного пространства.
Пусть система n векторов линейно-независима, а любая система n+1 векторов – линейно зависима, тогда число n называют размерностью пространства. dimV=n
Система этих n линейно-независимых векторов называется базисом линейного пространства. Рассмотрим систему n+1 векторов.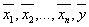
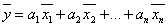 Такое представление называется разложение
Такое представление называется разложение 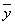 по базису, а числа
по базису, а числа 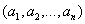 называют координатами вектора.
называют координатами вектора.  17. Вектор. Проекция вектора на ось.
17. Вектор. Проекция вектора на ось. Вектор– направленный отрезок, т.е. раз есть слово отрезок, значит есть начало и конец.
1. перенос отрезка при помощи параллельного переноса, не изменяет вектор.
2. вектор задается «длиной вектора» и направления.
3. если у вектора изменить направление на противоположное, то получаем противоположный вектор.
4. нулевой вектор – вектор, длина которого = 0 или начальная конечная точки совпадают. ( у нулевого вектора направление неопределенно).
Коллинеарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же прямой.
Примечание: если из двух коллинеарных векторов направление одинаковое, то вектора сонаправленные, а если противоположные, то называется противоположно-направленные.
Компланарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же плоскости.
Примечание: два вектора в пространстве всегда компланарны.
Примечание: два вектора называются равными, если они сонаправлены и равны по длине.

18. Линейные операции над векторами.
1. умножение вектора на число:
Результатом будет вектор, коллинеарный исходному (соноправленный в случае положительного множителя и противоположно-направленный – в случае отрицательного множителя), длина которого равна произведению модуля числового множителя на длину исходного модуля.
2. сумма двух векторов:
Есть вектор, получаемый из слагаемых при помощи правила параллелограмма или правила треугольника.

19. Линейная зависимость и независимость системы векторов.
Определение линейной зависимости системы векторов. Система векторов A1,A2,...,An называется линейно зависимой, если существует ненулевой набор
чисел λ1, λ2,...,λn,прикотором линейная комбинация векторов λ1*A1+λ2*A2+...+λn*An равна нулевому вектору, то есть система уравнений: A1x1+A2x2+...+Anxn =Θ имеет ненулевое решение.
Набор чисел λ1, λ2,...,λn является ненулевым, если хотя бы одно из чисел λ1, λ2,...,λnотлично от нуля.
Определение линейной независимости системы векторов. Система векторов A1,A2,...,An называется линейно независимой, если линейная комбинацияэтих векторов λ1*A1+λ2*A2+...+λn*An равна нулевому вектору только при нулевом наборе чисел λ1, λ2,...,λn, то есть система уравнений: A1x1+A2x2+...+Anxn =Θ имеет единственное нулевое решение.

20. Теорема об единственности разложения вектора по базису. Координаты вектора. Декартова система координат.
Базис пространства-совокупность линнезавис векторов, по которым можно разложить любой вектор этого пр-ва.
Базис 3x мерного пр-ва образует любая тройка некомпланарных векторов пр-ва.
Если  образуют базис в пространстве, то любой вектор
образуют базис в пространстве, то любой вектор 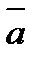 из этого пространства может быть представлен:
из этого пространства может быть представлен: 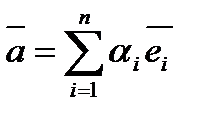
Примечание: для конкретно-заданного базиса не всегда просто бывает найти коэффициент 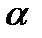 .
.
Проще всего это сделать когда базис является ортонормированным.
Понятие ортонормированности распадается на понятия ортогональности и нормированности.
( перпендикулярность и длина=1).
В 3-х мерном пространстве 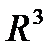 ортогональный базис состоит из 3 взаимноперпендикулярных векторов.
ортогональный базис состоит из 3 взаимноперпендикулярных векторов.
Ортонормированный базис состоит из 3-х взаимноперпендикулярных векторов, длина каждого из которых = 1.

21. Расстояние между двумя точками.
Расстояние d между точками A(x1, y1) и B(x2, y2) плоскости определяется по формуле:
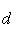
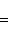
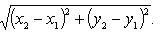

22. Деление отрезка в данном отношении.
Если x1 и y1 - координаты точки A, а x2 и y2 - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении 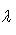
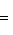
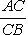 , определяются по формулам
, определяются по формулам 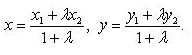 Если
Если 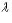
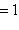 , то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам
, то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам 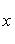
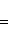
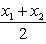 ;
; 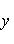
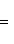
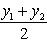

23. Направление вектора в пространстве.
Вектором называется упорядоченная пара точек. Перваяточка называется началомвектора, вторая — концом вектора. Расстояние между началом и концом вектора называется его длиной. Вектор, начало и конец которого совпадают, называется нулевым,его длина равна нулю.Если длина вектора положительна, то его называют ненулевым.Ненулевой вектор можно определить также как направленный отрезок, т.е. отрезок, у которого одна из ограничивающих его точек считается первой (началом вектора), а другая — второй (концом вектора). Направление нулевого вектора, естественно, не определено. 
