Интегралы и интегральные теоремы.
7.2.1.Убедиться, что поле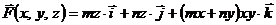 
потенциально, и найти его потенциал.
7.2.2.Даны: поле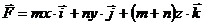 
и цилиндр D, ограниченный поверхностями z=0, z=m, x2+y2=(n+1)2. Найти:
а) поток поля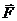 
через боковую поверхность цилиндра в направлении внешней нормали;
б) поток поля 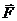через всю поверхность цилиндра в направлении внешней нормали непосредственно и с помощью теоремы Остроградского – Гаусса.
7.2.3. Даны поле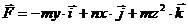 
и замкнутый виток 
, 
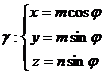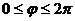( обход контура происходит в направлении, соответствующем возрастанию параметра φ). Найти циркуляцию поля 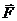вдоль контура γ непосредственно и с помощью теоремы Стокса.
Дифференциальные уравнения.
Уравнения первого порядка.
8.1.1.Найти общее решение уравнения:
а) 
; б) 
; в) 
.
8.1.2.Скорость роста банковского вклада пропорциональна с коэффициентом равным 
величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составляла 
миллионов рублей.
Линейные уравнения высших порядков.
8.2.1.Решить задачу Коши:
;
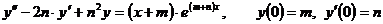Системы линейных уравнений.
8.3.1.Решить систему линейных уравнений
с начальными условиями 
.
9. Ряды.
Числовые ряды.
9.1.1.Исследовать на сходимость ряды с положительными членами:
а) 
; б) 
;
в) 
; г) 
.
9.1.2.Исследовать на условную сходимость и абсолютную сходимость знакочередующиеся ряды:
а) 
; б) 
.
Степенные ряды.
9.2.1.Найти область сходимости степенного ряда:
а) 
; б) 
.
9.2.2.Разложить функцию 
в ряд Тейлора в окрестности точки х0:
а) 
; б) 
.
9.2.3.С помощью разложения в ряд вычислить приближенно с точностью 0,001 значения:
а) 
; б) 
.
Ряды Фурье.
9.3.1.Разложить функцию в ряд Фурье в указанном интервале:
а) 
в интервале 
;
б) 
в интервале 
.
в) 
в интервале 
.
Функции комплексного переменного.
Действия с комплексными числами.
10.1.1. Выполнить действия:
а)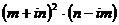 
; б)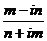 
.
10.1.2. Решить уравнения:
а)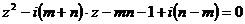 
; б)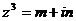 
.
Аналитические функции.
10.2.1. Показать, что функция 
аналитична.
10.2.2. Известна вещественная часть u(x,y)=m(x2-y2)+mx-ny аналитической функции f(z), (z=x+iy). Найти функцию f(z).
Интегрирование функций комплексного переменного.
10.3.1. Вычислить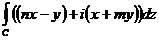 
, где контур С – незамкнутая ломанная, соединяющая точк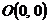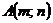и 
, 
и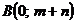 
.
10.3.2. Вычислить с помощью интегральной формулы Коши
.
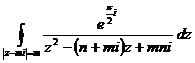Ряды Тейлора и Лорана.
10.4.1. Разложить функцию 
в окрестности точки 
в ряд Тейлора и найти радиус сходимости ряда.
10.4.2. Разложить функцию 
в окрестности точки в ряд Лорана.
10.4.3. Разложить функцию 
в ряд Лорана по степеням 
и найти область сходимости ряда.
Вычеты и их приложения.
10.5.1. Определить тип особых точек функции 
и найти вычеты в конечных особых точках.
10.5.2. Вычислить с помощью вычетов 
, где контур C, заданный уравнением 
, обходится против часовой стрелки.
Операционное исчисление.
Нахождение изображений и восстановление оригиналов.
11.1.1. Найти изображения функций:
а)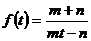 
; б)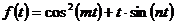 
.
11.1.2. Восстановить оригиналы по изображениям:
а)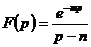 
; б)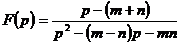 
.
Приложения операционного исчисления.
11.2.1. Решить операционным методом дифференциальное уравнение:
а)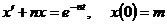 
;
б)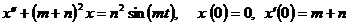 
.
12. Теория вероятностей.
Случайные события.
12.1.1. В коробке находятся m+2 синих, n+3 красных и 2n+1 зеленых карандашей. Одновременно вынимают m+3n+2 карандашей. Найти вероятность того, что среди них будет m+1 синих и n+1 красных.
12.1.2. В первой урне находятся m+2 шаров белого и n шаров черного цвета, во второй — m+n белого и m синего, в третьей — n+3 белого и m+1 красного цвета. Из первой и второй урны наудачу извлекают по одному шару и кладут в третью. После этого из третьей вынимают один шар. Найти вероятность того, что он окажется белым.
12.1.3. Вероятность попадания стрелка в мишень при одном выстреле равна 
. Производится n+4 выстрела. Найти вероятность того, что он промахнется не более двух раз.
Случайные величины.
12.2.1. Случайная величина Х равна числу появлений «герба» в серии из n+3 бросаний монеты. Найти закон распределения и функцию распределения F(x) этой случайной величины; вычислить ее математическое ожидание MXи дисперсию DX; построить график F(x).
12.2.2. Закон распределения дискретной случайной величины X имеет вид:
| xi | -2 | -1 | m | m+n | |
| pi | 0,2 | 0,1 | 0,2 | p4 | p5 |
Найти вероятности p4, p5, и дисперсию DX, если математическое ожидание MX=-0,5+0,5m+0,1n.
12.2.3. Плотность распределения непрерывной случайной величины X имеет вид:
Найти:
а) параметр а; б) функцию распределения 
;
в) вероятность попадания случайной величины X в интервал
;
г) математическое ожидание MX и дисперсию DX.
Построить график функций и .
12.2.4. Случайные величины 
имеют равномерное, пуассоновское и показательное распределения соответственно. Известно, что математические ожидания Mξi=m+n, а дисперсия Dξ1=n2/3. Найти вероятности: а) 
; б) 
; в) 
.