Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки A(x₁, y₁) и B(x₂, y), такие что x₁ ≠ x₂ и y₁ ≠ y₂ то уравнение прямой можно найти, используя следующую формулу

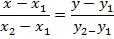
Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.

_{46.Взаимное расположение прямых на плоскости}

Прямые l₁ и l₂ либо совпадают, либо параллельны, либо пересекаются в одной точке, либо скрещиваются (т.е. не лежат в одной плоскости). Покажем, как распознать эти четыре случая. Отметим, что в первых трёх случаях прямые l₁ и l₂ лежат в одной плоскости.
1)Прямые l1 и l2 лежат в одной плоскости ⇔ три вектора A₁A₂ ,s₁ и s₂компланарны ⇔ их смешанное произведение равно нулю:₍A₁A₂ s₁s₂)=0
2)Прямые l₁ и l₂ совпадают ⇔ три вектора A₁A₂ ,s₁ и s₂коллинеарные, т.е. их координаты пропорциональны.

3) Прямые l₁ и l₂ параллельны ⇔ векторы s₁ и s₂ коллинеарны, т.е. их координаты пропорциональны, но они не коллинеарны вектору A₁A₂.

4) Прямые l₁ и l₂ пересекаются в одной точке ⇔ три вектора A₁A₂ ,s₁ и s₂ компланарны, т.е. ₍A₁A₂ s₁s₂)=0, но векторы s₁ и s₂не коллинеарны, т.е. их координаты не пропорциональны.

5) Прямые l₁ и l₂скрещиваются, т.е. они не лежат в одной плоскости⇔ три вектора A₁A₂ ,s₁ и s₂ не компланарны ⇔их смешанное произведение не равно нулю: ₍A₁A₂ s₁s₂)≠0
47.Условия параллельности и ортогональности прямых на плоскости.

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов 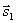и :

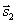Две прямые параллельнытогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l₁ параллельна l₂ тогда и только тогда, когда 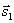параллелен .

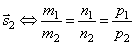Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .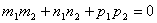

48.Угол между прямыми на плоскости.
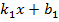y= , y= 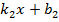Обозначим через угол ψ,отсчитываемый от первой прямой ко второй в том направлении, в котором производиться кратчайший поворот от первого базисного вектора ко второму; 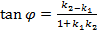( если знаменатель 0,то прямые перпендикулярны) Две прямые параллельны, если k₁ = k₂ . Две прямые перпендикулярны, если k₁ = -1/ k₂ .

49.Условие параллельности 2-х прямых в пространстве.

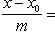
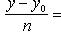
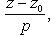
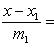
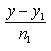
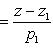,имеет вид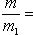

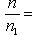
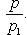
1)Если прямые параллельны, то они образуют с осью OX одинаковые углы. Поэтому угловые коэф-ты k1 и k2 этих прямых равны. Обратно, если k1= k2,то углы наклона прямых к оси OX одинаковы, откуда следует, что данные прямые параллельны. Условием параллельности 2-х прямых яв-ся равенство их угловых коэффициентов. (Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = lА, В₁ = lВ.)
50.Условие совпадения2-х прямых в пространстве.
Если 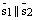, т.е есл 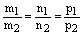и , то прямые либо совпадают: 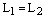, либо параллельны: 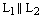. Определить, какой из этих двухслучаев имеет место быть, очень просто. Если точка 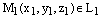лежит и на прямой 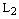, т.е. ее координаты удовлетворяет уравнениям прямой 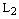: 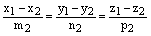, то прямые совпадают.

51.Условие пересечения 2-х прямых в пространстве.
Если 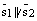(не перпендикулярны), то прямые либо скрещиваются, либо пересекаются. Если прямые пересекаются, то обе они лежат в одной плоскости и, следовательно, векторы 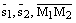компланарные
( прямые пересекаются в одной точке тогда и только тогда, когда )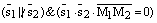
52.Условие скрещивающихся прямых в пространстве.
Если 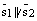(,не перпендикулярны), то прямые либо скрещиваются, либо пересекаются,когда прямые скрещиваются, векторы 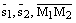некомпланарные. (прямые скрещиваются тогда и только тогда, когда )

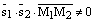53.Угол между прямыми в пространстве.

Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида

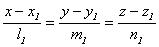и 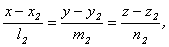косинус угла между ними можно найти по формуле:

= .

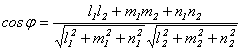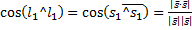_{54.Условие параллельности прямой и плоскости}

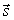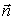Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.

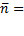{A,B,C}

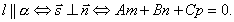
_{55.Условие принадлежности прямой плоскости.}

сли 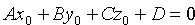, то уравнение (12.20) имеет вид 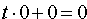; ему удовлетворяет любое значение t, любая точка прямой является точкой пересечения прямой и плоскости. Заключаем: прямая лежит в плоскости. Таким образом, одновременное выполнение равенств

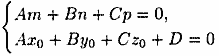
является условием принадлежности прямой плоскости.

56.Условие ортогональности прямой и плоскости
Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

условием перпендикулярности прямой и плоскости – условие параллельности этих векторов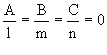
_{57.Задача о вычислении угла, образованного прямой и плоскостью.}

Угол θ между прямой и плоскостью есть угол между этой прямой и её проекцией на данную плоскость.

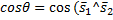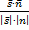)= ; sin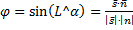

Если направляющий вектор прямой выбрать так, чтобы cos 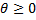,и взять 0 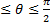, то угол между прямой и плоскостью дополняет θ до

Матрицы. Виды матриц.