Простейшие свойства вероятности: монотонность, формула сложения, вероятность разности событий.

Вывод формул и св-а сочет-й

1. С катое в степени 0 = С катое в степ к =1

2. С катое в первой = к

3.

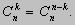
Доказательство.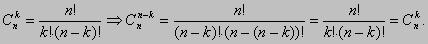

4 . ( ).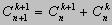

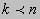Доказательство.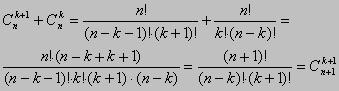

Последнее свойство позволяет описать процедуру последовательного получения числа сочетаний при различных значениях n и k.

Используя последнее свойство, можно представить число сочетаний в виде так называемого треугольника Паскаля.

5.Геометрическая вероятность Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности -вероятность попадания точки в область(отрезок, часть плоскости и т.д.). Пусть отрезок l составляет часть отрезка L. На отрезок L на удачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством. P= Длинаl/длинаL

Простейшие свойства вероятности: монотонность, формула сложения, вероятность разности событий.

Если А Ì В, то Р(А) £ Р(В), т.е. вероятность монотонна. Представим множество В как В = А + B\A (см. рисунок 1). По построению А(В\А)=Æ, следовательно, события А и В\А несовместны. Поэтому по аксиомам конечной аддитивности^* и неотрицательности вероятности имеем Р(В) = Р(А) + Р(В\А) ³ Р(А).

Р(А) £ 1 для любого А Î F. Так как A Ì W, то из свойства монотонности и аксиомы нормировки вероятности следует Р(А) £ Р(W) = 1. Формула сложения и вероятность разности событий:

Р(А+В) = Р(А) + Р(В) – Р(АВ) для любых А, В Î F. Представим А в виде А = А\В + АВ (см. рисунок 2). Очевидно, что события А\В и АВ несовместны. Тогда по аксиоме конечной аддитивности вероятности имеем Р(А) = Р(А\В) + Р(АВ),откуда Р(А\В)=Р(А)-Р(АВ). Аналогичным образом поступим с событием А+В. Имеем А+В = В + А\В, причем события В и А\В несовместны. Тогда из аксиомы конечной аддитивности вероятности следует Р(А+В)=Р(В)+Р(А\В). Подставляя в данное выражение формулу для Р(А\В), получаем требуемое. Р(А+В)=Р(А)+Р(В)-Р(АВ).

^* Аксиома: Для любых несовместных событий А и В из F справедливо равенство Р(А + В) = Р(А) + Р(В).

Доказательство

Рассмотрим один из возможных случаев, возникший в результате того, что процесс оказался в состояниях A₁, ..., A_m соответственно x₁, ..., x_m раз. Вероятность этого конкретного случая равна 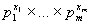. Однако процесс может оказаться в состояниях A₁, ..., A_m соответственно x₁, ..., x_m раз несколькими способами. Число таких конкретных способов будет равно 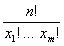. Из этого следует, что вероятность возникновения любого из этих конкретных состояний, при которых процесс может оказаться в состояниях A₁, ..., A_mсоответственно x₁, ..., x_m раз равна 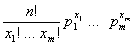. Конечная формула совпадает с формулой плотности полиномиального распределения.

Теорема Пуассона.

Теорема Пуассона: Между биномиальным распределением и распределением Пуассона имеется следующая связь: Пусть n ® µ, p ® 0 и при этом np º a = const. Тогда:

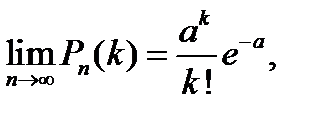
Где .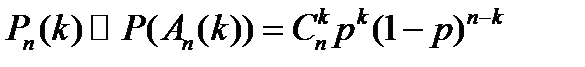

Доказывается эта теорема с использованием второго замечательного предела (1-a/n)ⁿ ® e^-a при n ® µ.

Дискретная СВ Х с реализациями xk = k, k = 0, 1, …, имеет распределение Пуассона с параметром a > 0, что символически записывается как Х ~ П(а), если

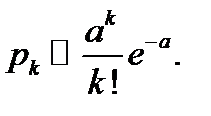
M[X] = D[X] = a.

Эта теоре­ма дает пуассоновское приближение биномиального распределения и обычно используется при p<0,1 и npq 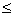9

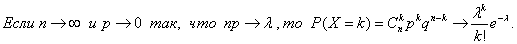
Локальная

Если вероятность наступления события А в каждом из n независимых испытаний равна p (p¹0, p¹1), а число испытаний достаточно велико, то справедлива формула:

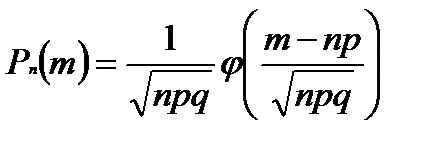
где 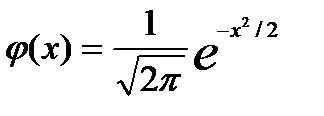- малая функция Лапласа

Замечание: формула 2 исп, когда n³10, np>10

Интегральная.

Если число повторных независимых испытаний достаточно велико, вероятность появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что в этих испытаниях событие А появится число раз, заключенное в границах [a;b], может быть посчитана по формуле:

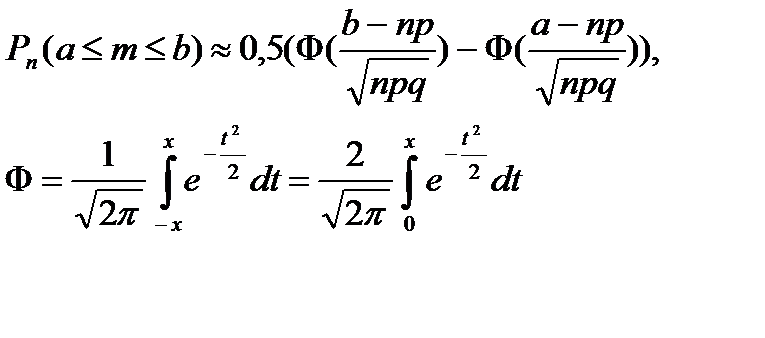Свойства функции Лапласа:

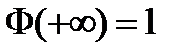
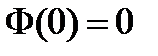
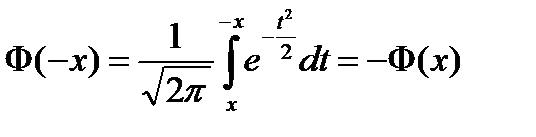
Функция нечетная, возрастающая

X>4, Ф(х)=1 Следствие из интегральной теоремы Муавра-Лапласа. Если число повторных независимых испытаний достаточно велико, вероятность появления события А в каждом испытании постоянно и отлично от нуля и единицы, то вероятность того, что число появлений события А отклонится от произведения np не больше, чем на некоторое положительное число r по модулю, может быть посчитано по формуле

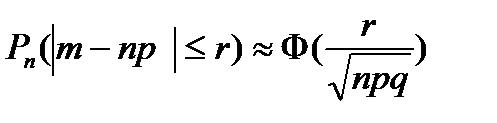
Статистическое распределение выборки. Варианты. Полигон и гистограмма.

Статистическим распределением выборки.Статистическим распределением выборкиназывают пе­речень вариант и соответствующих им частот или относи­тельных частот. Статистическое распределение можно за­дать также в виде последовательности интервалов и соответ­ствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал). Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математи­ческой статистике — соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами. Статистическое распределение записывается в виде таблицы: 1 строка – варианты; 2 строка – частоты.

n – объем выборки(частота).Иногда вместо частот используют относительную частоту:W_i = n_i / n;ΣWi = 1 Разность между наибольшим и наименьшим элементами выборки называется размахом выборки, т.е. R = x_max-x_min

При большом объеме выборки ее элементы объединяются в группы. В процессе группированного ряда подсчитываются также накопленные частоты. ñ_i* - частота i-интервала равна сумме частот: ñ₃* = ñ₁+*ñ₂*+ñ₃*

Ŵi*- накопленная относительная частота.

Полигономчастот называется ломаная линия, вершинами которой служат точки с координатами (х_i;n_i), i=1…k.Для группировки выборки строят гистограмму частот, т.е. ступенчатую фигуру, состоящую из прямоугольников,площадь прямоугольника равна частоте ñ_i*.Площадь гистограммы равна объему выборки.

Высота прямоугольников равна ñ*_i / n.

Геометрическая вероятность

Формула полной вероятности

Теорема Пуассона.

Локальная

Статистическое распределение выборки. Варианты. Полигон и гистограмма.

Вывод формул и св-а сочет-й

1. С катое в степени 0 = С катое в степ к =1

2. С катое в первой = к

3.

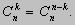
Доказательство.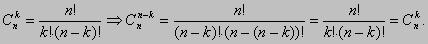

4 . ( ).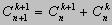

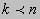Доказательство.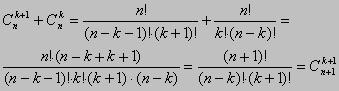

Последнее свойство позволяет описать процедуру последовательного получения числа сочетаний при различных значениях n и k.

Используя последнее свойство, можно представить число сочетаний в виде так называемого треугольника Паскаля.

5.Геометрическая вероятность Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности -вероятность попадания точки в область(отрезок, часть плоскости и т.д.). Пусть отрезок l составляет часть отрезка L. На отрезок L на удачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством. P= Длинаl/длинаL

Простейшие свойства вероятности: монотонность, формула сложения, вероятность разности событий.

Если А Ì В, то Р(А) £ Р(В), т.е. вероятность монотонна. Представим множество В как В = А + B\A (см. рисунок 1). По построению А(В\А)=Æ, следовательно, события А и В\А несовместны. Поэтому по аксиомам конечной аддитивности^* и неотрицательности вероятности имеем Р(В) = Р(А) + Р(В\А) ³ Р(А).

Р(А) £ 1 для любого А Î F. Так как A Ì W, то из свойства монотонности и аксиомы нормировки вероятности следует Р(А) £ Р(W) = 1. Формула сложения и вероятность разности событий:

Р(А+В) = Р(А) + Р(В) – Р(АВ) для любых А, В Î F. Представим А в виде А = А\В + АВ (см. рисунок 2). Очевидно, что события А\В и АВ несовместны. Тогда по аксиоме конечной аддитивности вероятности имеем Р(А) = Р(А\В) + Р(АВ),откуда Р(А\В)=Р(А)-Р(АВ). Аналогичным образом поступим с событием А+В. Имеем А+В = В + А\В, причем события В и А\В несовместны. Тогда из аксиомы конечной аддитивности вероятности следует Р(А+В)=Р(В)+Р(А\В). Подставляя в данное выражение формулу для Р(А\В), получаем требуемое. Р(А+В)=Р(А)+Р(В)-Р(АВ).

^* Аксиома: Для любых несовместных событий А и В из F справедливо равенство Р(А + В) = Р(А) + Р(В).