Теорема сложения вероятностей.

Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

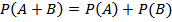
Условная вероятность. Теорема умножения вероятностей определение независимых случайных событий.

Произведения событий А и В называется событием состоящем в появлении этих событий.

События А и В называются независимыми, когда события независят от другого.

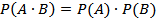
Формула полной вероятности

Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) B₁, В₂,...,В_n, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:

Р(А) = Р (В₁) Р_В1(А) + Р (В₂) Р_В2(А) + ... + Р (В_n) Р_Вn(А). (*)

где Р(В₁)+Р(В₂)+...+Р(В_n)=1.

Формула Байеса

,

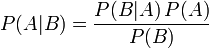где

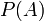— априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

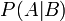— вероятность гипотезы A при наступлении события B (апостериорная вероятность);

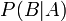— вероятность наступления события B при истинности гипотезы A;

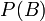— полная вероятность наступления события B.

Формула Бернулли

Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность 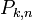того, что событие A наступит k раз в n независимых испытаниях, равна: 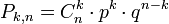, где .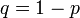

Дискретные случайные величины. Таблица распределения

ОПРЕДЕЛЕНИЕ. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:

X	x1	x2	...	xn
P	p1	p2	...	pn

Функция распределения дискретной СВ.

0, если x<X₁

P₁, если x₁<x<x₂

P₁+P₂, если х₂<x<x₃

F(x) …

P₁+P₂+P₃+…+P_n-1, если х_n-1<x<x_n

1, если x>x₁

Математическое ожидание дискретной СВ.

ОПРЕДЕЛЕНИЕ. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина Х может принимать только значения х₁, х₂, х₃,...,х_nвероятности которых соответственно равны p₁, p₂, p₃,...,p_n. Тогда математическое ожидание М(х) случайной величины Х определяется равенством:

M(x)=х₁p₁+х₂p₂+...+х_np_n

Свойства математического ожидания

1. Математическое ожидание постоянной величины равно самой постоянной М(С)=С.

2. Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X)

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY)=M(X)•M(Y).

4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: M(X+Y)=M(X)+M(Y).