Угловой коэффициент в уравнении прямой. Геометрический смысл коэффициента.

Преобразуем уравнение прямой ax + by + c=0 к виду

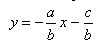
Введем обозначения

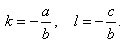
Тогда получим y = kx + l.

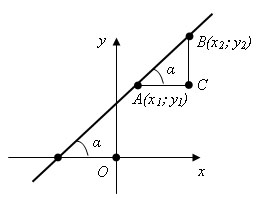
Возьмем две точки на прямой A (x1; y1) и B (x2; y2), такие что x1 < x2.
Их координаты удовлетворяют уравнению прямой:

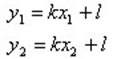
Вычитая эти равенства почленно, получим

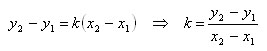
Проведя прямую через точку A параллельно оси x и прямую через точку B параллельную оси y, мы получим треугольник ABC. Замечаем, что

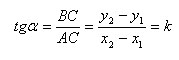
Если прямая расположена следующим образом :

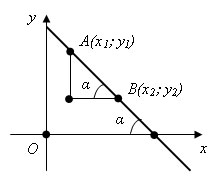
То

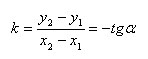
Таким образом, коэффициент k в уравнении прямой с точностью до знака равен тангенсу острого угла, который образует прямая с осью x.
Коэффициент k в уравнении прямой называется угловым коэффициентом прямой.

5 ВОПРОС:

Угол между двумя прямыми. Условия перпендикулярности и параллельности двух прямых.
Углом между двумя прямыми называют угол между их направляющими векторами. Пусть относительно ПДСК заданы две прямые своими каноническими уравнениями: l1: (x-x1)/a1=(y-y1)/b1=(z-z1)/c1, l2: (x-x2)/a2=(y-y2)/b2=(z-z2)/c2, пересекающиеся в некоторой точке M0. a1={a1, b1, c1}, a2={a2, b2, c2}. cos(a1,^a2)=(a1•a2)/(|a1|•|a2|)=(a1a2+b1b2+c1c2)/(√(a12+b12+c12)•√(a22+b22+c22)). Из данной формулы следует, что две прямые перпендикулярны тогда и только тогда, когда a1a2+b1b2+c1c2=0.
Две прямые параллельны тогда и только тогда, когда a1/a2=b1/b2=c1/c2

Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую.

Если прямая параллельна плоскости проекции (h | | П1), то для того чтобы определить расстояние от точки А до прямой h необходимо опустить перпендикуляр из точки А на горизонталь h.

Нажмите на картинку для просмотра...

На ортогональном чертеже строим отрезок A1M1 перпендикулярно h1. Далее на прямой h1 откладываем отрезок M1M0 равный А2В2. Длину перпендикуляра АM можно найти способом прямоугольного треугольника А1M1M0: |АM| = |А1M0|.

Рассмотрим более сложный пример, когда прямая занимает общее положение. Пусть необходимо определить расстояние от точки М до прямой а общего положения.

Нажмите на картинку для просмотра...

Решение задачи проводится по следующей схеме: 1. Через заданную точку M проводится плоскость s перпендикулярная заданной прямой а. Плоскость задается двумя пересекающимися прямыми, фронталью (f) и горизонталью (h): s = h f. 2. Находится точка пересечения (K) исходной прямой а с плоскостью s. 3. Определяется расстояние от точки М до точки K способом прямоугольного треугольника. Длина гипотенузы прямоугольного треугольника M2K2N2 равна расстоянию от точки M до прямой а: |MK| = M2N2.

Задача на определение расстояния между параллельными прямыми решается аналогично предыдущей. На одной прямой берется точка, из нее опускается перпендикуляр на другую прямую. Длина перпендикуляра равна расстоянию между параллельными прямыми.

Гл 1

Гл 2

Гл 3

Гл 4

Гл 5

Гл 6

Гл 7Гл 8 Гл 9

6 ВОПРОС:

Свойства параболы:

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

y² = 2px называемая каноническим уравнением параболы

7 ВОПРОС:

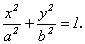называемая каноническим уравнением эллипса

8 ВОПРОС:

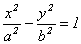- каноническое уравнение гиперболы.

9 ВОПРОС:

Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0 (3.1)

задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.

Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения (3.1):

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

10 ВОПРОС:

Пусть даны векторы 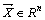и .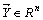
Определение. Суммой векторов 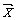и 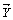называется вектор 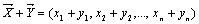, т.е. при сложении векторов их соответствующие координаты складываются: (2, –4) + (–2, 4) = (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2, –6,5).
Определение. Произведением вектора 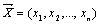на число 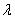называется вектор 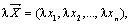т.е. при умножении вектора на число каждая его координата умножается на это число.
Можно проверить, что введенные таким образом операции над векторами удовлетворяют всем свойствам операций в линейном пространстве. Следовательно, арифметическое n-мерное пространство Rⁿ является частным случаем введенного ранее линейного пространства.
Определение. Скалярным произведением двух векторов 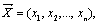и 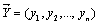называется число, равное сумме произведений соответствующих координат векторов: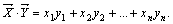
Пример: Пусть 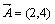и .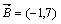
Тогда .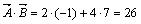
Скалярное произведение обладает следующими свойствами:
1. 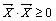, причем 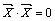, только при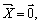
2. ,
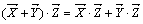3. ,
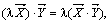4. .
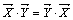Определение. Два вектора называются ортогональными, если их скалярное произведение равно 0, т.е. .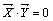
Пример. Пусть Тогда 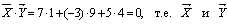ортогональны.
Определение. Линейное пространство с введенным скалярным произведением называется евклидовым n-мерным пространством.
Примеры:
1. Множество трехмерных векторов R³.
2. Множество двумерных векторов R².
3. Множество R¹ = R – множество действительных чисел.

11 ВОПРОС:

Скалярное произведение

Скалярное произведение векторов 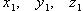и :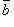

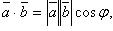
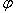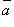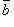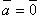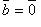где - угол между векторами и ; если либо , то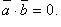

Из определения скалярного произведения следует, что 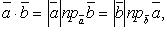где, например, 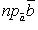есть величина проекции вектора 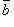на направление вектора .

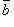Скалярный квадрат вектора: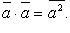

Свойства скалярного произведения: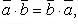

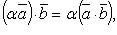
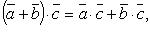
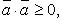
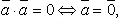
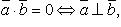
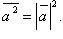
Скалярное произведение в координатах

Если 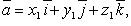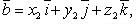то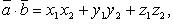

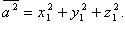
Угол между векторами

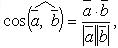
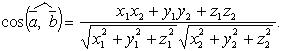
Векторное произведение

Векторное произведение векторов 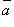и 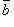- вектор, обозначаемы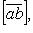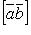й или 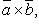для когорого:

1) 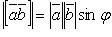( 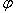- угол между векторам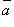и и , );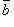

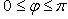2)

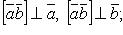
3) тройка 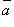, , 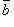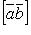- правая.

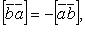
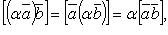
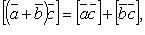
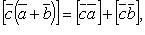
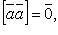
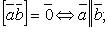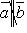Свойства векторного произведения: если , то 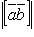равен площади параллелограмма, построенного на приведенных к общему началу векторах 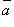и .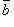

Норма — структура длины векторов на линейном пространстве.

Норма в векторном линейном пространстве 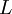над полем вещественных или комплексных чисел есть функция 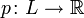, удовлетворяющая следующим условиям (аксиомы нормы):

1. 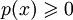, причём p(x) = 0 только при ;

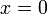2. 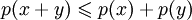для всех 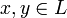(неравенство треугольника);

3. 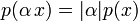для любого скаляра α.

Норма 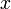обычно обозначается 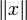. Линейное пространство с нормой называется нормированным пространством, а условия (1-3) — также аксиомами нормированного пространства.

Аксиома 2 обеспечивает выпуклость шаров 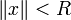, аксиома 3 — кроме прочего, их центральную симметрию.

Любой ненулевой вектор (в частности функцию) конечной нормы можно нормировать, поделив его на значение его нормы (после чего он станет нормированным). Также, нередко применяется выражение «нормированный на», подразумевающее, что норма объекта равна в этом случае не единице, а другой определенной величине. Например, иногда говорят о нормировании на дельта-функцию, когда речь идет о нормировании базиса функций, нумерованного непрерывным параметром.

12 ВОПРОС:

МАТРИЦА [matrix] — система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы. Таблица имеет следующий вид: