Определение предела функции.
Определение предела функции.
Число А называется пределом функции f(x) при х стремящимся к а, если для любого числа эбсилент >0, найдется такое число дельта, зависящее от эпсилент, что как только |x-a| будет меньше дельта (х не равен а) то тут же f(x) по модулю будут меньше эбсилант
А=Limx-af(x)
VE>0
Существует δ(E)>0; любой х принадлежащий Х; |x-a|< δ; (x не равен а)
=>|f(x)-A|<E
2.Операции над пределами.
Пусть существует предел функции f(x), при х стремящимся к а, равным А и существует предел функции g(x)=B, при х стремящимся к а, равный В, тогда существует предел функции f(x+g(x)), при х стремящимся к а, равный А=В
Существует limx-af(x)=F; существует limx-ag(x)=B
1) limx-a|f(x)+g(x)|=A+B
2) limx-af(x)*g(x)=AB
3) B не равен 0=> limx-a(f(x)/g(x))=A/B
Бесконечно малые и бесконечно большие пределы.
Функция α(х) называется бесконечно малой в точке а, х-а, если ее предел=0
Функция α(х) называется бесконечно большой в точке а, х-к бесконечности.
Теорема:
Пусть α(х) бесконечно малая в точке а, тогда 1/ α(х)- бесконечно большая, и наоборот если f(x)- бесконечно большая в точке а, то 1/ α(х)- бесконечно малая.
Вывод: если х стремится к бесконечности, и в числители и в знаменателе некоторые многочлены, а числитель> знаменателя, то предел = отношению коэффициента при старших степенях. Если степени числителя < степени знаменателя, то предел =0.
Первый замечательный предел.
Предел при х-0; Limx-0(sinx/x)=1
X, sinx- эквивалентные малые единицы, х примерно равен sinx
5. Второй замечательный предел.
Limx-∞(1+1/x)=е (е- иррациональное число)- бесконечная непериодическая дробь
е=2,71728192…
Logea= lna
Непрерывность функции.
Непрерывность функции- функция f(x) называется непрерывной точкой в хо, если существует предел функции. Limx-xof(x)=f(xo)
Существует теорема:
Все элементарные функции непрерывны в области своего определения.
7. Классификация точек разрыва функции.
1) разрыв первого рода: скачок. Limx-xo-of(x)≠Limx+xof(x)
2) Разрыв второго рода, или бесконечный разрыв имеет место тогда, когда хотя бы один из односторонних пределов бесконечны F(x)=1/x
3) Точки устранимого разрыва. Имеет место тогда, кода существует предел Limx-xof(x)≠f(xo)
F(x)=sinx/x.
Sinx/x, где х≠0, 1, где х=0
Теоремы о непрерывности функции.
Теорема Больцамо-Коши
Пусть ф-ция f(x) непрерывна на отрезке ав и на концах отрезка принимает разные знаки, тогда существует точка С из интервала ав, в которой значение этой ф-ции =0.
Теорема:
Если ф-ция непрерывна на отрезке ав и f(а)= А, а F(b)=B, если A<B, то для любого С существует точка с из интервала ав, такая, что f(c)=C
Первая теорема Веерштрассе:
Если ф-ция f(x) не прерывна на отрезке ав, то она ограничена на этом отрезке. Существуют числа m,M, такие что m≤f(x)≤M
Вторая теорема Веерштрассе:
Если ф-ция непрерывна на отрезке ав, то она достигает на этом отрезке своего минимума и максимума. Т.е. существует в точке х1 их2 отрезки, такие, что f(x1)=m; f(x2)=M
Определение производной ф-ции.
Пусть функция f(x) непрерывна на интервале ав и точка хо принадлежит ав, выберем число дельтаХ такое, что х0+дельтаХпринадлежат ав, тогда величина дельтаХ называется приращением аргумента х в точке х0.
10. Дифференцируемость функции.
Функция f(x) называется дифференцированной в точке х0, если ее приращениев той точке может быть представлено в виде как некоторое число А*дельтаХ+£(дельтах)
Дельтаf(х0)= А*дельтаХ+£(дельтах)
Дифференциал функции.
Дифференциалом функции f(х) называется главное, линейное относительно приращение элемента часть приращения функции.
Теорема: если функция дифференцириума на интервале ав, то она непрерывна на этом интервале.
12. Производные и дифференциалы высших порядков.
Пусть u(x) и v(x)- две дифференцируемые функции в точке х, т.е. для них существуют производные, тогда: 1) (u+v)΄=u΄+v΄, сумма тоже дифференцируема;
2) (uv)΄=u΄v+uv΄ так же дифференцируема. Следствие если с константа, то (c*u) ΄=c*u΄
3) если v≠0, то (u/v) ΄=(u΄v-uv΄)/v²
Пусть функция y=f(x) дифференциривана в точке х, в свою очередь в х есть некая функция x=φ(t), деференцируема в точке t, тогда функцию у можно записать у=f(φ(t)) при этом функция у будет дифференцируема от t (y΄t=fx΄(x)-φt΄(t))/
Функция f называется внешней, а функция φ- внутренней.
Признак выпуклости функции.
Говорят, что функция на интервале ав выпукла вверх (вниз), если ее график лежит выше (ниже) касательной графиков в любой точке этого интервала.
Точка на график ф-ции, в которой выпуклость вверх переходит в выпуклость вниз или наоборот называется точкой перегиба графикаю
Теорема: пусть функция y=f(x) дважды дифференцирована на интервале ав. Для того, чтобы ф-ця f(x0 на интервале ав была выпукла вверх ( вниз), необходимо и достаточно, чтобы f’’(x)≤0, (f”’(x)≥0)
Асимптоты графика функции.
Асимптотой графика функции называется прямая расстояние от которой до точки на графике функции стремится к 0, при бесконечном удалении точки на графике от начла координат.
Асимптоты бывают: горизонтальные, вертикальные и наклонные.
Вертикальная асимптота: х=а, где а- точка бесконечного графика ( разрыв второго рода)
Наклонные асимптоты: у=kx+b, где k- определяется из условия k=limx-±∞(f(x)-k(x))
17. Первообразная. Неопределенный интеграл. Свойства неопределенного интеграла.
Пусть ф-ция f(x) непрерывна на интервале ав, ф-ция F(x) называется первообразной для ф-ции f(x), если выполняется равенство: F’(x)=f(x)
Ясно, что если с- любое число ( постоянная величина), то F(x)+c- так же будет первообразная для f(x) (F(x)+C)’=F’(x)+C’=f(x) т.е. если ф-ция f(x) существует хотя бы 1 первообразную, то их будет бесконечное множество и все они будут отличаться друг от друга на некоторое число С.
Пусть ф-ция f(x) непрерывна на интервале ав, тогда совокупность всех первообразных для нее называется неопределенным интегралом и обозначается: ⌠f(x)dx=F(x)+C
Вычисление неопределенного интеграла называется интегрированием.
Свойства неопределенного интеграла:
1) ⌠f(x)dx=⌠dF(x)=F(x)+C
2) (⌠f(xdx)’=(F(x)+C)’=f(x)
3) ⌠(f(x)+g(x))dx=⌠f(x)dx+⌠g(x)dx
4) ⌠λf(x)dx=λ⌠f(x)dx+⌠g(x)dx
Формула Ньютона-Лейбница
Если 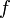 непрерывна на отрезке
непрерывна на отрезке 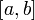 и
и 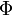 — ее любая первообразная на этом отрезке, то имеет место равенство
— ее любая первообразная на этом отрезке, то имеет место равенство
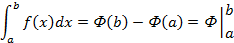
Линейное ДУ первого порядка
Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид
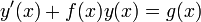
Формулы комбинаторики
· Размещение:
Размещение из n по m элементам называется любая упорядоченная выборка содержащая m-элементов.
Любые 2 размещения считаются различными, если они отличаются друг от друга составом или порядком следования элементов.
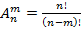
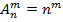
· Перестановка:
Перестановкой из n-элементов называется размещение из n по m.
2 любые перестановки отличаются только порядком следования элементов.
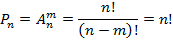
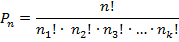
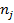 - количество повторений j-ого элемента.
- количество повторений j-ого элемента.
· Сочетание:
Сочетание из n-элементов по m-элементам называется любое подмножество одного множества. Два любых элемента отличаются друг от друга хотя бы элементом.
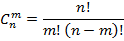
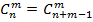
Формула полной вероятности
Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) B1, В2,...,Вn, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
Р(А) = Р (В1) РВ1(А) + Р (В2) РВ2(А) + ... + Р (Вn) РВn(А). (*)
где Р(В1)+Р(В2)+...+Р(Вn)=1.
Формула Байеса
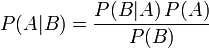 ,
,
где
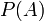 — априорная вероятность гипотезы A (смысл такой терминологии см. ниже);
— априорная вероятность гипотезы A (смысл такой терминологии см. ниже);
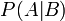 — вероятность гипотезы A при наступлении события B (апостериорная вероятность);
— вероятность гипотезы A при наступлении события B (апостериорная вероятность);
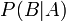 — вероятность наступления события B при истинности гипотезы A;
— вероятность наступления события B при истинности гипотезы A;
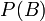 — полная вероятность наступления события B.
— полная вероятность наступления события B.
Формула Бернулли
Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность 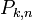 того, что событие A наступит k раз в n независимых испытаниях, равна:
того, что событие A наступит k раз в n независимых испытаниях, равна: 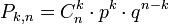 , где
, где 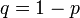 .
.
Дискретные случайные величины. Таблица распределения
ОПРЕДЕЛЕНИЕ. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:
| X | x1 | x2 | ... | xn |
| P | p1 | p2 | ... | pn |
Определение предела функции.
Число А называется пределом функции f(x) при х стремящимся к а, если для любого числа эбсилент >0, найдется такое число дельта, зависящее от эпсилент, что как только |x-a| будет меньше дельта (х не равен а) то тут же f(x) по модулю будут меньше эбсилант
А=Limx-af(x)
VE>0
Существует δ(E)>0; любой х принадлежащий Х; |x-a|< δ; (x не равен а)
=>|f(x)-A|<E
2.Операции над пределами.
Пусть существует предел функции f(x), при х стремящимся к а, равным А и существует предел функции g(x)=B, при х стремящимся к а, равный В, тогда существует предел функции f(x+g(x)), при х стремящимся к а, равный А=В
Существует limx-af(x)=F; существует limx-ag(x)=B
1) limx-a|f(x)+g(x)|=A+B
2) limx-af(x)*g(x)=AB
3) B не равен 0=> limx-a(f(x)/g(x))=A/B
