Угол между прямой и плоскостью. Условие параллельности и перпендикулярности. Определение точек пересечения.

Ax+By+Cz+D=0

= =

sinφ=

sinφ=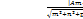

еслипрямая׀׀плоскостиs⊥nsn=0 mA+nB+pC=0

если прямая⊥плоскости s׀׀n

Определение точек (решить совместно)

Ax+By+Cz+D=0

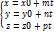
A(x₀+mt)+B(y₀+nt)+C(z₀+pt)+D=0

Окружность. Определение. Вывод канонического уравнения

Окружность – множество точек в плоскости, стоящих от центра на одно и то же расстояние (r)

О(a,b) центр окружности и ОМ=r, M(x,y)

r²= (x-a)²+(y-b)²

Эллипс. Определение. Вывод канонического уравнения. Исследование формы эллипса

Эллипсом называется множество точек в плоскости, сумма расстояний которых от двух данных точек называемых фокусами, есть величина постоянная, равная 2а, больше чем расстояние между фокусами

=1

Симметрия. Т.к. уравнение эллипса содержит только квадраты текущих координат, он будет симметричен относительно Ох и Оу

Точки пересечения у=0 и х=0

Эллипс расположен в прямоугольнике образованного прямыми х=±а, у=±b

Вывести у

Эксцентриситетом, обозначается ε, называется отношение расстояний между фокусами и длине большей оси эллипса

Гипербола. Определение. Вывод канонического уравнения. Исследование формы гиперболы

Гипербола – множество точек в плоскости, модуль разности расстояний от которых до двух данных точек называемых фокусами есть величина постоянная = 2а

= 1

Т.к. х и у в уравнении в квадрате, значит гипербола будет симметрична относительно Ох и Оу

Точки пересечения гиперболы с осями называются вершинами гиперболы, с осью Оу гипербола пересечений не имеет

Вывести у

Парабола. Определение. Вывод канонического уравнения

Парабола – это множество точек, расстояние которых до некоторых точек называемых фокусами и до некоторой прямой называемой директрисой равно.

y² = 2 p x

Парабола проходит через начало координат

Парабола симметрична оси Ох

Если р>0, то ветви параболы направлены вправо

Исследование общего уравнения линии второго порядка в случае отсутствия члена с произведением текущих координат

Ax²+2Bxy+Cy²+2Dx+2Ey+N=0

A,B,C≠0

Сфера. Определение. Вывод канонического уравнения.

Сфера – это множество точек стоящих от центра на одно и то же расстояние r

r²= (x-a)²+(y-b)²+(z-c)²

Цилиндрические поверхности

Поверхность образованная движением образующей (L), которая перемещается в пространстве, сохраняя при это направление и каждый раз пересекая направляющую (K) называется цилиндрической поверхностью или цилиндр

Название цилиндра определяется названием образующей: Эллиптическая (по эллипсу, уравнение эллипса), Круговая…

Эллипсоиды

=1

Гиперболоид

= 1

Параболоид

x²+y²=2px

Конические поверхности

Поверхность, образуемая движением линии АВ , перемещающуюся в пространстве так, что она постоянно проходит через вершину и пересекает направляющую

Функция. Основные понятия. Способы ее задания

Функция- соответствие f, которое каждому элементу x сопоставляет только один у

Множество Х называется областью определения

Множество У называется областью значения

Если элементами х и у являются действительные числа то функция называется числовой

Три способа задания функции: графический, аналитический, табличный