Множества. Операции над множествами. Символика математической логики.
Множество - это совокупность объектов, рассматриваемая как одно целое. Понятие множества принимается за основное, т. е. не сводимое к другим понятиям. Объекты, составляющие данное множество, называются его элементами.
Ниже перечислены основные операции над множествами:
объединение:
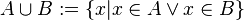
пересечение:
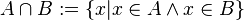
разность:
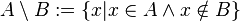
симметрическая разность:
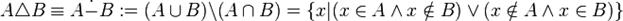
дополнение:
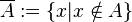
Операция дополнения подразумевает некоторый универсум (множество U, которое содержит A):
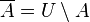
Декартово или прямое произведение:
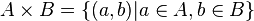
| мвол (TeX) | Название | Значение |
| Произношение | ||
| Раздел математики | ||
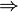 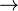 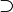 | Импликация, следование | 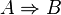 означает «если означает «если 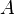 верно, то верно, то 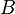 также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначениянадмножества, см. ниже.). также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначениянадмножества, см. ниже.). |
| «влечёт» или «если…, то» | ||
| везде | ||
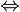 | Равносильность |  означает « означает « 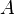 верно тогда и только тогда, когда верно тогда и только тогда, когда 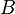 верно». верно». |
| «если и только если» или «равносильно» | ||
| везде | ||
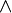 | Конъюнкция | 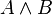 истинно тогда и только тогда, когда истинно тогда и только тогда, когда 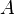 и и 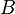 оба истинны. оба истинны. |
| «и» | ||
| Математическая логика | ||
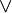 | Дизъюнкция | 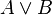 истинно, когда хотя бы одно из условий истинно, когда хотя бы одно из условий 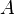 и и 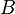 истинно. истинно. |
| «или» | ||
| Математическая логика | ||
 | Отрицание | 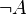 истинно тогда и только тогда, когда ложно истинно тогда и только тогда, когда ложно 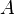 . . |
| «не» | ||
| Математическая логика | ||
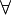 | Квантор всеобщности | 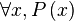 обозначает « обозначает « 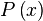 верно для всех верно для всех 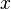 ». ». |
| «Для любых», «Для всех», «Для всякого» | ||
| Математическая логика | ||
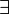 | Квантор существования | 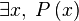 означает «существует хотя бы один означает «существует хотя бы один 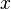 такой, что верно такой, что верно 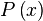 » » |
| «существует» | ||
| Математическая логика | ||
 | Равенство | 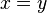 обозначает « обозначает « 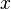 и и 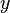 обозначают одно и то же значение». обозначают одно и то же значение». |
| «равно» | ||
| везде | ||
| «Множество всех… таких, что верно…» | ||
| Теория множеств | ||
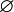 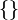 | Пустое множество | 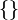 и и 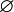 означают множество, не содержащее ни одного элемента. означают множество, не содержащее ни одного элемента. |
| «Пустое множество» | ||
| Теория множеств | ||
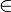 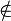 | Принадлежность/непринадлежность к множеству | 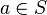 означает « означает « 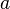 является элементом множества является элементом множества 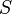 » » 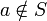 означает « означает « 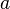 не является элементом множества не является элементом множества 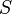 » » |
| «принадлежит», «из» «не принадлежит» | ||
| Теория множеств | ||
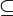 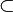 | Подмножество | 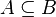 означает «каждый элемент из означает «каждый элемент из 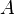 также является элементом из также является элементом из 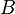 ». ». 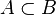 обычно означает то же, что и обычно означает то же, что и 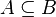 . Однако некоторые авторы используют . Однако некоторые авторы используют 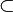 , чтобы показать строгое включение (то есть , чтобы показать строгое включение (то есть 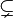 ). ). |
| «является подмножеством», «включено в» | ||
| Теория множеств | ||
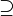 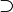 | Надмножество | 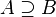 означает «каждый элемент из означает «каждый элемент из 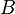 также является элементом из также является элементом из 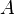 ». ». 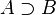 обычно означает то же, что и обычно означает то же, что и 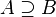 . Однако некоторые авторы используют . Однако некоторые авторы используют 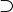 , чтобы показать строгое включение (то есть , чтобы показать строгое включение (то есть 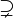 ). ). |
| «является надмножеством», «включает в себя» | ||
| Теория множеств | ||
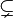 | Собственное подмножество | 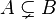 означает означает 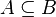 и и 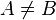 . . |
| «является собственным подмножеством», «строго включается в» | ||
| Теория множеств | ||
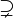 | Собственное надмножество | 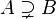 означает означает 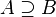 и и 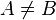 . . |
| «является собственным надмножеством», «строго включает в себя» | ||
| Теория множеств | ||
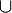 | Объединение | 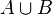 означает множество элементов, принадлежащих означает множество элементов, принадлежащих 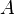 или или 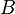 (или обоим сразу). (или обоим сразу). |
| «Объединение … и …», «…, объединённое с …» | ||
| Теория множеств | ||
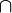 | Пересечение | 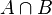 означает множество элементов, принадлежащих и означает множество элементов, принадлежащих и 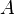 , и , и 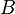 . . |
| "Пересечение … и … ", «…, пересечённое с …» | ||
| Теория множеств | ||
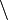 | Разность множеств | 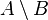 означает множество элементов, принадлежащих означает множество элементов, принадлежащих 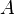 , но не принадлежащих , но не принадлежащих  . . |
| «разность … и …», «минус», «… без …» | ||
| Теория множеств | ||
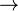 | Функция(отображение) | 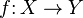 означает функцию означает функцию 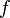 с областью определения с областью определения 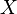 иобластью значений иобластью значений 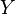 . . |
| «из … в …», | ||
| везде | ||
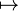 | Отображение | 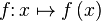 означает, что образом означает, что образом 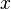 после применения функции после применения функции 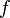 будет будет 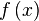 . . |
| «отображается в» | ||
| везде | ||
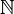 | Натуральные числа | 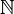 означает множество означает множество 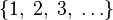 или реже или реже 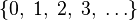 (в зависимости от ситуации). (в зависимости от ситуации). |
| «Эн» | ||
| Числа | ||
 | Целые числа | 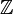 означает множество означает множество 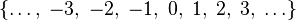 |
| «Зед» | ||
| Числа | ||
 | Рациональные числа |  означает означает 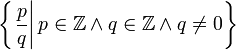 |
| «Ку» или «Къю» | ||
| Числа | ||
 | Вещественные (действительные) числа | 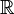 означает множество всех пределов последовательностей из означает множество всех пределов последовательностей из 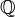 |
| «Эр» | ||
| Числа | ||
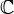 | Комплексные числа | 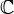 означает множество означает множество 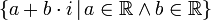 |
| «Це» | ||
| Числа | ||
 | Кватернионы | 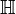 означает множество означает множество 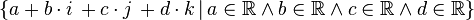 |
| «Аш» | ||
| Числа | ||
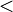 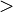 | Сравнение | 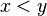 обозначает, что обозначает, что 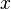 строго меньше строго меньше 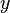 . . 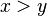 означает, что означает, что 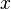 строго больше строго больше 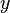 . . |
| «меньше чем», «больше чем» | ||
| Отношение порядка | ||
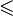 или или 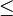 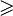 или или 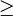 | Сравнение | 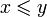 означает, что означает, что 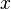 меньше или равен меньше или равен 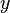 . . 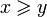 означает, что означает, что 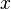 больше или равен больше или равен 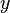 . . |
| «меньше или равно»; «больше или равно» | ||
| Отношение порядка | ||
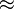 | Приблизительное равенство | 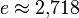 с точностью до 10−3 означает, что 2,718 отличается от с точностью до 10−3 означает, что 2,718 отличается от  не больше чем на 10−3. не больше чем на 10−3. |
| «приблизительно равно» | ||
| Числа | ||
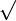 | Арифметическийквадратный корень | 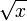 означает неотрицательное действительное число, которое в квадрате даёт означает неотрицательное действительное число, которое в квадрате даёт 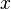 . . |
| «Корень квадратный из …» | ||
| Числа | ||
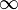 | Бесконечность | 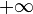 и и 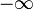 суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. |
| «Плюс/минус бесконечность» | ||
| Числа | ||
 | Абсолютная величина(абсолютное значение, модуль) числа, илимощность множества | 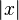 обозначает абсолютную величину обозначает абсолютную величину 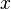 . . 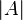 обозначает мощность множества обозначает мощность множества 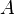 и равняется, если и равняется, если 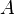 конечно, числу элементов конечно, числу элементов 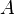 . . |
| «Модуль»; «Мощность» | ||
| Числа и Теория множеств | ||
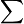 | Сумма (набора чисел), суммаряда | 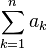 означает «сумма означает «сумма 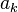 , где , где 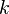 принимает значения от 1 до принимает значения от 1 до 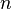 », то есть », то есть 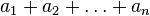 . . 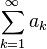 означает сумму ряда, состоящего из означает сумму ряда, состоящего из 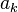 . . |
| «Сумма … по … от … до …» | ||
| Арифметика,Математический анализ | ||
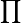 | Произведение | 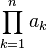 означает «произведение означает «произведение 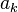 для всех для всех 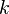 от 1 до от 1 до 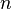 », то есть », то есть 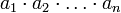 |
| «Произведение … по … от … до …» | ||
| Арифметика | ||
 | Факториал | 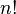 означает произведение всех натуральных чисел от 1 до означает произведение всех натуральных чисел от 1 до 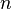 включительно, то есть включительно, то есть 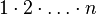 |
« 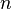 факториал» факториал» | ||
| Комбинаторика | ||
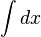 | Интеграл | 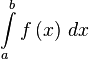 означает «интеграл от означает «интеграл от 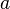 до до 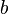 функции функции 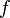 от от 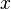 по переменной по переменной 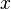 ». ». |
| «Интеграл (от … до …) функции … по (или d)…» | ||
| Математический анализ | ||
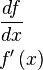 | Производная | 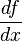 или или 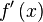 означает «(первая) производная функции означает «(первая) производная функции 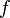 от от 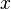 по переменной по переменной 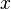 ». ». |
| «Производная … по …» | ||
| Математический анализ | ||
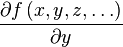 | Частная производная | 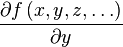 означает «(первая) частная производная функции означает «(первая) частная производная функции 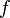 от переменных от переменных 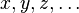 по переменной по переменной 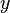 ». ». |
| «Частная производная … по …» | ||
| Математический анализ | ||
« 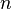 -я производная … по …» -я производная … по …» | ||
| Математический анализ |
