Перечень вопросов к экзаменам и зачету.
Начальник кафедры ВМ _______________ Тульчий В.В.
Доцент, к.ф-м.н.
Новороссийск
2013 год
Курс (экзамен).
Векторы. Линейно независимые системы векторов. Базис.
2. Скалярное, векторное, смешанное произведения векторов: определение, вычисление, свойства. Приложения.
3. Уравнения прямой в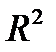 
. Угол между прямыми.
4. Уравнения плоскости в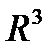 
. Расстояние от точки до плоскости. Угол между плоскостями. Условие∥и ⊥ плоскостей.
5. Уравнения прямой в пространстве 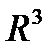. Угол между прямыми. Условия ∥и ⊥прямых.
6. Прямая и плоскость. Угол между прямой и плоскостью.
7. Общее уравнение кривых второго порядка.
8. Канонические уравнения окружности, эллипса, гиперболы, параболы. Геометрические свойства.
9. Поверхности второго порядка. Канонические формы уравнений.
10. Исследование поверхностей второго порядка методом сечений.
11. Множество вещественных чисел. Верхние и нижние грани множеств.
12. Числовые последовательности. Предел.
13. Число е. Натуральные логарифмы. Предел функции в бесконечности.
14. Свойства функций, имеющих предел. Формула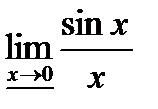 
.
15. Бесконечно малые функции и их свойства.
16. Связь между бесконечно большими функциями и бесконечно малыми.
17. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
18. Использование бесконечно малых функций при вычислении пределов.
19. Непрерывность функции в точке. Свойства функций, непрерывных в точке.
20. Непрерывность суммы, произведения и частного.
21. Точки разрыва функции и их квалификация.
22. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.
23. Производная функции, ее геометрический и механический смысл.
24. Правила дифференцирования.
25. Дифференцируемость функции. Дифференциал функции.
26. Связь дифференциала с производной.
27. Производные и дифференциалы высших порядков.
28. Формула Лейбница.
29. Теорема Ролля,
30. Теорема Лагранжа,
31. Теорема Коши.
32. Правило Лопиталя.
33. Представление функций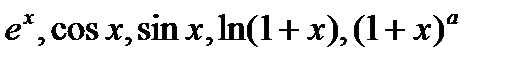 
по формуле Тейлора.
34. Приложение формулы Тейлора к приближенным вычислениям.
35. Исследование функций с помощьюпроизводных
36. Функции нескольких переменных. Область определения.
37. Предел функции нескольких переменных. Непрерывность.
38. Линии и поверхность уровня.
39. Частные производные.
40. Полный дифференциал и его связь с частными производными.
41. Касательная плоскость и нормаль к поверхности.
42. Геометрический смысл полного дифференциала.
43. Частные производные и полные дифференциалы высших порядков.
44. Формула Тейлора.
45. Экстремум функции нескольких переменных. Необходимое и достаточное условия.
46. Условный экстремум.
47. Метод множителей Лагранжа.
Курс (зачет).
1. Неопределенный интеграл, его свойства.
2. Таблица основных интегралов.
3. Замена переменной интегрирования.
4. Интегрирование по частям
5. Интегрирование простейших рациональных дробей.
6. Интегрирование рациональных функций
7. Определенный интеграл, его свойства.
8. Производная интеграла с переменным верхним пределом.
9. Формула Ньютона-Лейбница.
10. Вычисление определенного интеграла по частям и подстановкой.
11. Вычисление площадей плоских фигур и длин дуг кривых, уравнения которых заданы в декартовых координатах.
12. Вычисление площадей плоских фигур и длин дуг кривых, уравнения которых заданы в полярных координатах
13. Вычисление площадей плоских фигур и длин дуг кривых, уравнения которых заданы параметрических координатах
14. Диф. уравнения (ДУ) 1 порядка.
15. Задача Коши.
16. Теорема сущ. и единствен. решения задачи Коши.
17. ДУ с разделяющимися переменными.
18. Однородные ДУ.
19. Линейные ДУ.
20. Уравнение Бернулли.
21. ДУ в полных дифференциалах.
22. ДУ высших порядков. Задача Коши.
23. ДУ, допускающие понижение порядка Структура общего решения однородных ДУ.
24. Определитель Вронского и его свойства.
25. Линейные однородные ДУ с постоянными коэффициентами.
26. Случай действительных простых и кратных корней.
27. Случай комплексных корней.
28. Линейные неоднородные ДУ с постоянными коэффициентами и спец. правой частью.
29. Задачи, приводящие к понятию двойного интеграла, определение, свойства. Вычисление в декартовой и полярной системе координат.
30. Задачи, приводящие к понятию тройного интеграла, определение, свойства. Вычисление в декартовой, цилиндрической и сферической системе координат.
31. Задача о массе криволинейного стержня, приводящая к понятию криволинейного интеграла первого рода. Определение, свойства.
32. Задача о работе переменной силы, приводящая к понятию криволинейного интеграла второго рода. Определение, свойства.
33. Связь криволинейных интегралов 1-го и 2-го рода.
34. Формула Грина.
35. Геометрические приложения криволинейных интегралов.
36. Механические приложения криволинейных интегралов.
Курс (экзамен).
1. Числовые ряды. Сходимость и сумма ряда.
2. Необходимое условие сходимости. Действия над рядами.
3. Достаточные признаки сходимости для знакоположительных рядов: 1-ый признак сравнения; 2-ой (предельный) признак сравнения.
4. Признак Даламбера.
5. Радикальный признак Коши, интегральный признак Коши.
6. Знакопеременные ряды.
7. Абсолютная и условная сходимость.
8. Знакочередующиеся ряды.
9. Признак Лейбница.
10. Ряды с комплексными членами.
11. Понятие функциональных рядов. Область сходимости.
12. Понятие равномерной сходимости.
13. Признак Вейерштрасса.
14. Свойства равномерно сходящихся рядов.
15. Степенные ряды.
16. Теорема Абеля.
17. Радиус сходимости.
18. Свойства степенных рядов.
19. Ряды Тейлора и Маклорена.
20. Разложение функций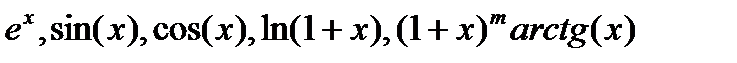 
в степенные ряды.
21. Тригонометрическая система функций и ее свойства.
22. Ряд Фурье. Разложение функций в ряд Фурье на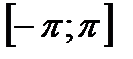 
.
23. Теорема Дирихле.
24. Испытания и случайные события: классификация, операции над событиями.
25. Классическое определение вероятности.
26. Геометрическая вероятность.
27. Теоремы сложения и умножения вероятностей.
28. Формула полной вероятности.
29. Теорема Байеса.
30. Формула Бернулли.
31. Формула Пуассона.
32. Локальная и интегральная теоремы Лапласа.
33. Свойства функции Лапласа.
34. Случайная величина.
35. Функции распределения и ее свойства.
36. Закон распределения дискретной случайной величины.
37. Математическое ожидание, дисперсия, среднее квадратическое отклонение дискретной случайной величины.
38. Распределение Пуассона, биноминальное распределение.
39. Непрерывные случайные величины.
40. Плотность распределения и ее связь с функцией распределения.
41. Математическое ожидание и дисперсия непрерывной случайной величины.
42. Равномерное, показательное, нормальное распределения.
43. Первое и второе неравенства Чебышева.
44. Предел вероятности. Принцип практической достоверности.
45. Понятие о теоретическом законе больших чисел.
46. Закон больших чисел в форме Чебышева.
47. Задачи математической статистики.
48. Точечные оценки и их свойства.
49. Свойства выборочного среднего и выборочной дисперсии.
50. Доверительный интервал для математического ожидания при большом и малом объемах выборочных наблюдений случайной величины.
51. Статистическая проверка гипотез.
52. Критерий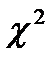 
; критерий Колмогорова.
53. Коэффициент корреляции.
54. Линейная регрессия.
55. Метод наименьших квадратов.
Требования к уровню освоения программы дисциплины.
Рекомендации по оценке знаний и умений учащихся по математике.
1. Содержание и объем материала, подлежащего проверке, определяется программой.
При проверке усвоения материала нужно выявлять полноту, прочность усвоения
студентами теории и умения применять ее на практике.
2. Основными формами проверки знаний и умений учащихся по математике являются
письменная контрольная работа и устный опрос.
3. При оценке письменных и устных ответов преподаватель в первую очередь учитывает
показанные студентами знания и умения. Оценка зависит также от наличия и характера
погрешностей, допущенных студентами.
4. Среди погрешностей выделяются ошибки и недочеты. Погрешность считается
ошибкой, если она свидетельствует о том, что студент не овладел основными
знаниями, умениями, указанными в программе.
5. К недочетам относятся погрешности, свидетельствующие о недостаточно полном или
недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний,
не и считающихся в программе основными. Недочетами также считаются:
погрешности, которые не привели к искажению смысла полученного задания или
способа его выполнения; неаккуратная запись; небрежное выполнение графика.
6. Граница между ошибками и недочетами является в некоторой степени условной. При
одних обстоятельствах допущенная погрешность может рассматриваться
преподавателем как ошибка, в другое время и при других обстоятельствах — как
недочет.
7. Задания для устного и письменного опроса студентов состоят из теоретических
вопросов и задач. Ответ на теоретический вопрос считается безупречным, если по
своему содержанию полностью соответствует вопросу, содержит все необходимые
теоретические факты, обоснованные выводы, а его изложение и письменная запись
математически грамотны и отличаются последовательностью и аккуратностью.
8. Решение задачи считается безупречным, если правильно выбран способ решения, само
решение сопровождается необходимыми объяснениями, правильно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
9. Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, т.е. за ответ выставляется одна из отметок: 1 (плохо), 2 (неудовлетворительно), 3 (удовлетворительно), 4 (хорошо), 5 (отлично).
10. Преподаватель может повысить оценку за оригинальный ответ на вопрос или оригинальное решение задачи, за решение более сложной задачи или ответ на более сложный вопрос, предложенные студенту дополнительно после выполнения им заданий.
Критерии ошибок.
К грубым ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской;
К негрубым ошибкам относятся потеря корня или сохранение в ответе постороннего корня; отбрасывание без объяснений одного из них и равнозначные им;
К недочетам относятся: нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях.
Оценка устных ответов студентов.
| Оценка «5» | - полно раскрыл содержание материала в объеме, предусмотренном программой и учебником, - изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику; - правильно выполнил рисунки, чертежи, графики, сопутствующие ответу; - показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания; - продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при отработке умений и навыков; - отвечал самостоятельно без наводящих вопросов преподавателя. Возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые студент легко исправил по замечанию преподавателя. |
| Оценка «4» | -если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков: - в изложении допущены небольшие пробелы, не исказившие содержание ответа; - допущены один – два недочета при освещении основного содержания ответа, исправленные по замечанию преподавателя; - допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию преподавателя. |
| Оценка «3» | - неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала; - имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов преподавателя; - студент не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме; - при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков. |
| Оценка «2» | - не раскрыто основное содержание учебного материала; - обнаружено незнание или непонимание студентом большей или наиболее важной части учебного материала; - допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов преподавателя. |
| Оценка «1» | - студент обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу. |