Оценка параметров генеральной совокупности. точечная оценка и ее свойства

Числовые характеристики генеральной совокупности называются параметрами генеральной совокупности.

Например, для нормального распределения это математическое ожидание и среднее квадратическое отклонение (СКО), для равномерного распределения – это границы интервала, в котором наблюдаются значения этой случайной величины

Оценка параметра – соответствующая числовая характеристика, рассчитанная по выборке. Если оценка определяется одним числом, она называется точечной оценкой.

Например, среднее арифметическое выборочных значений служит оценкой математического ожидания. Выборочные значения случайны, поэтому оценки можно рассматривать как случайные величины. Построим точечную оценку параметра 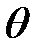по выборке 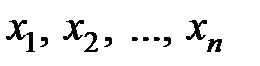как значение некоторой функции и перечислим «желаемые» свойства оценки .

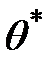Определение 4.1. Оценка 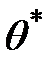называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра: .

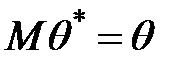Данное свойство характеризует отсутствие систематической ошибки, т.е. при многократном использовании вместо параметра 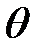его оценки 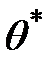среднее значение ошибки приближения 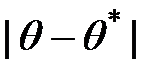равно нулю.

Так, выборочное среднее арифметическое 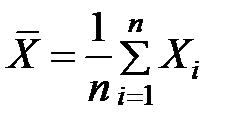является несмещенной оценкой математического ожидания, а выборочная дисперсия 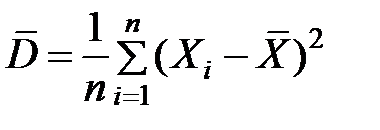– смещенная оценка генеральной дисперсии D. Несмещенной оценкой генеральной дисперсии является оценка («исправленная дисперсия»)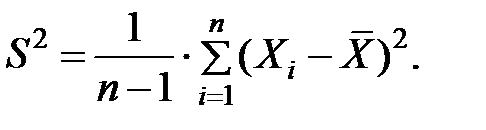

Определение 4.2. Оценка 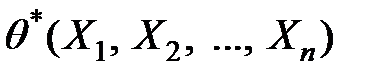называется состоятельной, если она сходится по вероятности к оцениваемому параметру 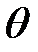при

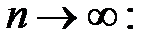
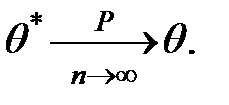
Данное свойство характеризует улучшение оценки с увеличением объема выборки.

Сходимость по вероятности означает, что при большом объеме выборки вероятность больших отклонений оценки от истинного значения мала.

Определение 4.3.. Несмещенная оценка является эффективной, если она имеет наименьшую среди всех несмещенных оценок дисперсию.

Пример 4.4.:

1. Вычислить среднее значение массы тела детей 6 лет.

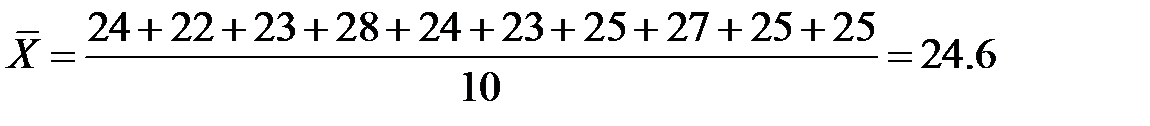
2. Если выборочное среднее вычисляется по вариационному ряду, то находят сумму произведений вариант на соответствующие частоты, и делят на количество элементов в выборке: .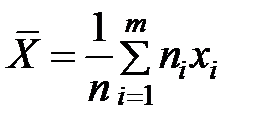

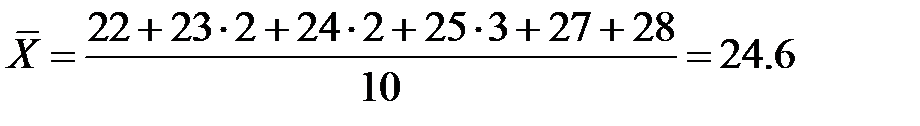
3. В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего значениями вариант считают середины интервалов. Так, для вычисления среднего значения массы тела женщин 30 лет из примера 4.3. используют формулу:

.

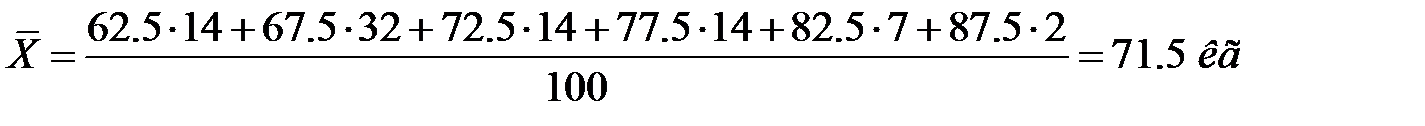Другими характеристиками являются модаи медиана.

В теории вероятностей модой М_о дискретной случайной величины называется ее значение, которое имеет максимальную вероятность. Модой непрерывной случайной величины называется такое ее значение, при котором достигается максимум плотности распределения 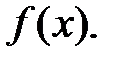Закон распределения называется унимодальным, если мода единственна. В математической статистике мода М_о определяется по выборке, как варианта с наибольшей частотой.

Медианой называется варианта, расположенная в центре ранжированного ряда. Если ряд состоит из четного числа вариант, то медианой считают среднее арифметическое двух вариант, расположенных в центре ранжированного ряда.

Пример 4.5. Найти моду и медиану выборочной совокупности по массе тела детей 6 лет.

Ответ: М_о = 24; М_е = 24.

Основные числовые характеристики выборочной совокупности:

1) размах вариационного ряда R=X_max – X_min. Этот показатель является наиболее простой характеристикой рассеяния и показывает диапазон варьирования величины. Этой характеристикой пользуются при работе с малыми выборками;

2) выборочное среднее находится как взвешенное среднее арифметическое 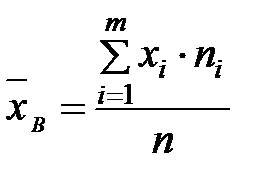, которое характеризует среднее значение признака X в пределах рассматриваемой выборки;

3) выборочная дисперсия определяется по формуле: 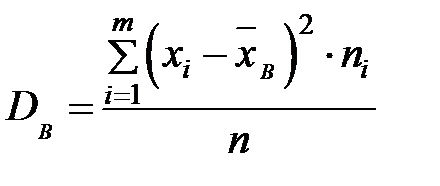, которая является мерой рассеяния возможных значений показателя X вокруг своего среднего значения, и ее размерность совпадает с квадратом размерности варианты;

4) выборочное среднее квадратическое отклонение 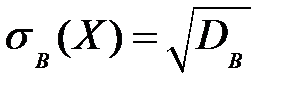описывает абсолютный разброс значений показателя X. Его размерность совпадает с размерностью варианты;

5) «исправленная» дисперсия (вычисляют при малых n, n<30) 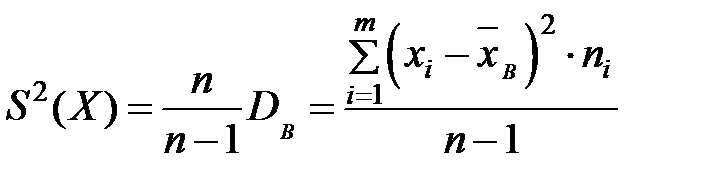и «исправленное» стандартное отклонение ;

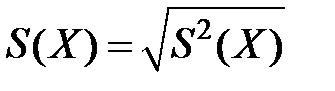6) коэффициент вариации 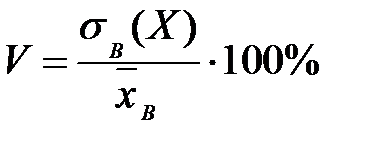характеризует относительную изменчивость показателя X, то есть относительный разброс вокруг его среднего значения 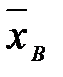. Коэффициент вариации является безразмерной величиной, поэтому он пригоден для сравнения рассеяния вариационных рядов, варианты которых имеют различную размерность.

Пример 4.6.: Измерена длина (Х) и масса тела (Y) девочек 10-ти лет. Получены следующие показатели: Х=130 см, s_Х = 5 см, Y = 32 кг, s_Y = 4 кг. Какая величина имеет большую вариативность?

Так как длина и масса тела измеряются в разных единицах, то вариативность нельзя сравнить при помощи СКО. Необходимо вычислить относительный показатель вариации.

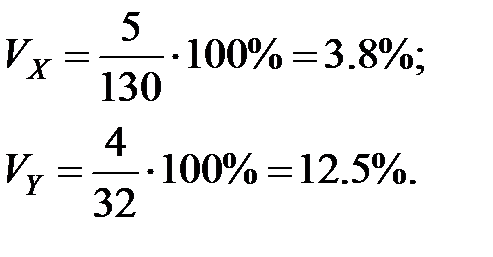
Таким образом, масса тела имеет большую вариативность, чем длина тела.

ОЦЕНКА С ПОМОЩЬЮ ИНТЕРВАЛОВ

Оценка параметров с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенными вероятностями (доверительными) находятся истинные значения оцениваемых параметров. Интервальная оценка определяется двумя числами - концами интервала.

Пусть найденная по данным выборки величина q^* служит оценкой неизвестного параметра q. Оценка q^* определяется тем точнее, чем меньше
|q - q^*|, т. е. чем меньше d в неравенстве |q - q^*|< d, d > 0.

Доверительной вероятностью (надежностью) оценки q^* параметра q называется вероятность ¡, с которой оценивается неравенство |q - q^*|< d.

Число a=1 - ¡ называется уровнем значимости, определяющим вероятность того, что оцениваемый параметр не попадет в доверительный интервал.

Обычно задается надежность ¡ и определяется d. Чаще всего вероятность ¡ задается значениями от 0.95 и выше. Неравенство |q - q^*|< d можно записать в виде

- d < q - q^* < d или q^* - d < q < q^* + d.

Доверительным интервалом называется интервал (q^* - d, q^* + d), который покрывает неизвестный параметр q с заданной надежностью.

Определение доверительного интервала для среднего значения нормально распределенной измеряемой случайной величины Х при известной дисперсии .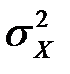

Нам уже известно, что 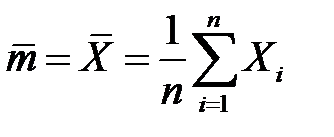. Можно показать [1-5], что 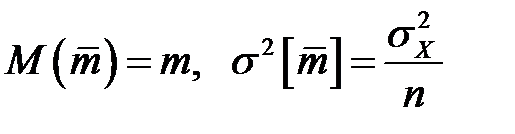(сумма 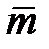нормально распределенных случайных величин 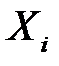сама является нормальной).

Зададим доверительную вероятность ¡ и найдем доверительный интервал ( 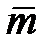- d, 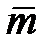+ d), который покрывал бы неизвестный параметр 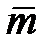с заданной надежностью ¡.

Согласно формуле В (свойства нормального распределения, раздел 3)

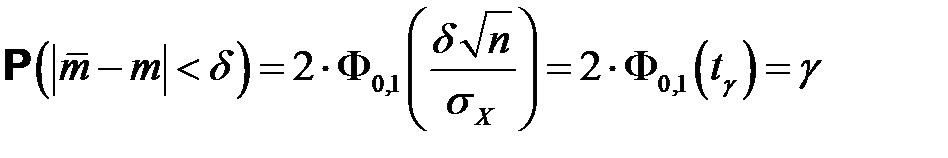. (4.1)

Таким образом, для отыскания величины доверительной границы случайного отклонения результатов наблюдений по доверительной вероятности ¡ имеем уравнение:

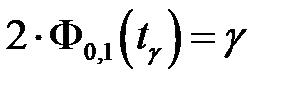, где ,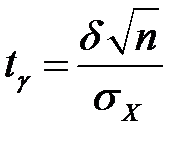

где значение 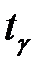находим по таблице Лапласа (приложение 1), .

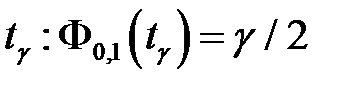Пример 4.7. По результатам наблюдений была найдена оценка неизвестного математического ожидания m случайной величины 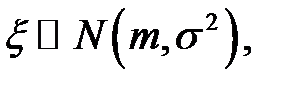если точечная оценка 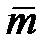=10.2, а дисперсия оценки 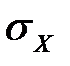=4. Требуется оценить доверительныйинтервал для оценки математического ожидания по 36-ти наблюдениям с заданной надежностью ¡=0.99.

Решение. Из (4.1) следует, что 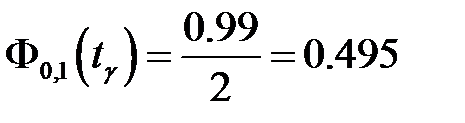. Отсюда получаем, что 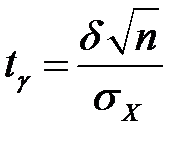=2.58 и половина искомого интервала 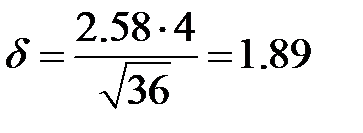. Так как 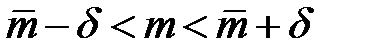, то с вероятностью 0.99 доверительныйинтервал для оценки математического ожидания: .

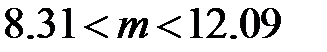Со случаем, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна, можно ознакомится в [3, 4, 6].