Если все конъюнкции ДНФ - простые мпликанты, и если удаление из нее любой конъюнкции даст ДНФ неэквивалентную исходной, то такая форма называется тупиковой ДНФ (ТДНФ).

В ТДНФ нельзя удалить ни одну букву и ни одну конъюнкцию.

Рассмотрим примеры.

Пусть 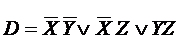- СДНФ (совокупность всех простых импликант) с

М₁(D)=(000,001,011, 111).

Покажем, что D не тднф.

Возьмем 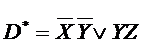,М₁(D*) = (000,001,111).

Следовательно, D* = D, а значит D не тднф.

Теперь проверим, является ли D* - ТДНФ.

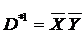, М₁(D*¹) = (000,001) - D*¹ 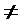D, а является импликантой D.

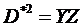, М₁(D*²) = (011,111) - D*² 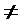D, а является импликантой D.

Следовательно, из D* нельзя удалить ни одну букву и ни одну конъюнкцию и она является ТДНФ для D.

Аналогично можно доказать, что МДНФ обязательно является ТДНФ.

В тоже время нельзя утверждать, что любая ТДНФ является МДНФ.

У БФ может быть много ТДНФ, при этом часть из них (или все) могут быть МДНФ.

Рассмотрим пример.

Для F(x,y,z) с М₁ = (001,010,011,100,101,110) можно построить СДНФ равную

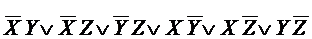
Эта бф имеет две МДНФ:

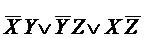и

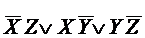
Кроме того, БФ имеет 3 тднф, не являющихся мднф

,

,

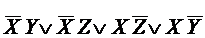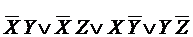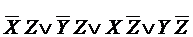
Пути решения задачи упрощения ДНФ БФ.

Основная проблема при работе с БФ – это проблема минимизации.

Существует различные способы минимизации. Рассмотрим основные принципы некоторых из них.

Первый способ. В данном случае исходной является ДСНФ. По ней строится СДНФ, а из СДНФ получают несколько ТДНФ, и из них производится выбор МДНФ или кратчайшей ДНФ.

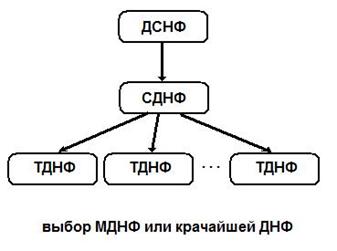
Для «почти всех БФ» переход от ДСНФ к СДНФ сопровождается усложнением, так как длина СДНФ составляет, по крайней мер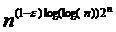е, , где .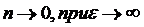

При этом конъюнкции СДНФ имеют не менее (n-logn-1), букв.

Несмотря на это СДНФ при поиске МДНФ необходимо получать, так как в общем случае не имея всех простых импликант, нельзя найти МДНФ.

Число ТДНФ для «почти всех БФ» очень велико.

При этом минимальных или кратчайших ДНФ очень мало. Перебрав небольшое число ТДНФ нельзя статистически достоверно получить МДНФ.

Но, встречающиеся на практике БФ таковы, что СДНФ у них, не слишком сложны, а расхождения в числе букв у МДНФ и наиболее сложной ТДНФ не слишком велики.

В связи с этим на практике используются и другие методы упрощения ДНФ.

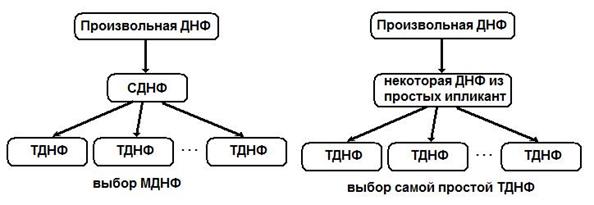
Нахождение ТДНФ для задач большой размерности может быть выполнено следующим образом: для произвольной ДНФ производится получение простых импликант, а затем удаление избыточных конъюнкций. Таким образом, получается произвольная ТДНФ.

Построение СДНФ по ДСНФ.

СДНФ строят, используя разные подходы, но при этом, можно выделить два основных:

1) Генерация всех возможных конъюнкций исходных переменных и проверка их на наличие свойств простой импликанты рассматриваемой БФ;

2) Формирование всех простых импликант БФ по конъюнкциям из исходной ДСНФ (либо некоторой ДНФ) БФ.

Первый подход порождает много разных методов, отличающихся по организации перебора вариантов при генерации кодов конъюнкций. Эти методы наиболее удобны и эффективны при «машинном» решении задач.

Проверки конъюнкций чаще всего выполняют по М₀.

Рассмотрим пример.

Пусть F(X,Y,Z) имеет М₁=(001, 010,011,100,101,110) и, соответственно, М₀=(000,111).

Необходимо определить является ли конъюнкция 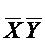простой импликантой БФ F.

Для переменных (X,Y,Z) М₁( 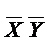)=(000, 001).

Так как 000 - набор из М₀(F), то М₁( 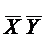) 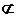М₁(F).

Следовательно, 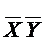не является импликантой F, а тем более простой импликантой.

Второй подход проиллюстрируем с помощью метода построения СДНФ по ДСНФ, предложенного Квайном и усовершенствованного Мак-Класки.