Дизъюнктивная нормальная форма (днф).

Имея БФ, мы можем представить ее в виде ДСНФ, но такая форма не является единственной.

Пусть ДСНФ некоторй функции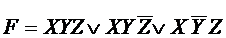

Так как А А = А, можно представить F в виде:

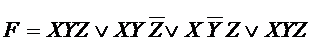
Далее с, помощью скобочных преобразований, можно получить:

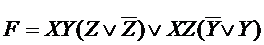
В полученном выражении меньше букв и операций чем в исходном.

Так как А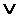 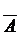=1, то дальнейшие преобразования приведут нас к форме:

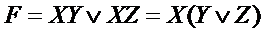
Здесь еще меньше букв и операций. Таким образом, была выполнена минимизация исходной БФ.

Минимизация БФ подразумевает упрощение формул (при сохранении их эквивалентности) в определенном классе формул и при определенном способе подсчета сложности.

В качестве формул в теории БФ чаще всего рассматривают бесскобочные выражения вида «дизъюнкция конъюнкций» (аналог в обычной алгебре – сумма произведений), так как простые скобочные формы удобно строить из простых бесскобочных.

Ведем определения, касающиеся минимизации БФ.

Конъюнкция называется элементарной, если каждая переменная входит в нее только один раз.

Дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).

Длиной ДНФ называется число конъюнкций, из которых она состоит.

ДНФ, имеющая наименьшую длину среди всех эквивалентных, называется кратчайшей.

ДНФ, имеющая наименьшее число букв среди всех эквивалентных, называется минимальной ДНФ (МДНФ).

МДНФ может не быть кратчайшей и наоборот.

ДНФ D называется ДНФ БФ F, если М₁ для D совпадает с М₁ БФ F ( М₁(D)=М₁(F)).

БФ Ф называется импликантой БФ F, если множество наборов М₁(Ф) является частью (подмножеством) множества наборов М₁(F).

Обозначается это как: М₁(Ф) 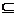М₁(F).

Рассмотрим пример.

Пусть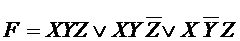

Ф₁= XY; Ф₂= YZ;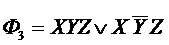

M₁(Ф₁) = 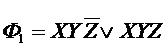=(110, 111)

M₁(Ф₂) = 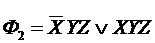= (011, 111)

M₁(Ф₃) = 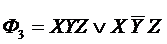= (101, 111)

M₁(F) = (101, 110,111)

Ф₁ и Ф₃ являются импликантами F, так как их множества М1, являются частью М1 функции F.

Ф₂ не является импликантой F, так как один набор из М1 (011), не входит в М1 функции F.

Простая импликанта - неукорачиваемая конъюнкция – из нее нельзя удалить ни одной переменной.

Конъюнкция К является простой импликантой БФ F, если:

1) К - импликанта БФ F ;

2) Любая К*, состоящая из части букв К, не является импликантой БФ F.

Рассмотрим пример простой импликанты.

X	Y	Z	F

Предположим, что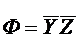- простая импликанта БФ F.

Докажем это.

1) М₁(F) = (000,001,010,011,100)

М₁(Ф) = (000,100)

Следовательно, Ф является импликантой F.

2) Из Ф можно получить две более короткие конъюнкци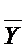и: и .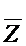

M₁(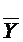) = (000,001,100,101)

M₁(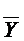) 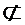M₁(F) следовательно, 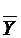не является импликантой F.

M₁(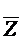) = (000,010,100,110)

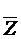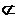
M₁() M₁(F) следовательно, 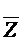не является импликантой F.

Следовательно из Ф нельзя удалить ни одной переменной.

Из 1) и 2) следует, что Ф простой импликантой F.

ДНФ, состоящая из всех простых импликант бф, называется сокращенной ДНФ (СДНФ).

Число букв в СДНФ может быть не только меньше, но и больше чем у ДСНФ. Слово «сокращенная» говорит о том, что в ДСНФ используются максимально укороченные (сокращенные) конъюнкции.